§ 39. Geometrie.
[150] Eben so beruht auf dem Nexus der Lage der Theile des Raums die ganze Geometrie. Sie wäre demnach eine Einsicht in jenen Nexus: da solche aber, wie oben gesagt, nicht durch bloße Begriffe möglich ist, sondern nur durch Anschauung; so müßte jeder geometrische Satz auf diese zurückgeführt werden, und der Beweis bestände bloß darin, daß man den Nexus, auf dessen Anschauung es ankommt, deutlich heraushöbe; weiter könnte[150] man nichts thun. Wir finden indessen die Behandlung der Geometrie ganz anders. Nur die zwölf Axiome Euklids läßt man auf bloßer Anschauung beruhen, und sogar beruhen von diesen eigentlich nur das neunte, elfte und zwölfte auf einzelnen verschiedenen Anschauungen, alle die andern aber auf der Einsicht, daß man in der Wissenschaft nicht, wie in der Erfahrung, es mit realen Dingen, die für sich neben einander bestehn und ins Unendliche verschieden seyn können, zu thun habe; sondern mit Begriffen, und in der Mathematik mit Normalanschauungen, d.h. Figuren und Zahlen, die für alle Erfahrung gesetzgebend sind und daher das Vielumfassende des Begriffs mit der durchgängigen Bestimmtheit der einzelnen Vorstellung vereinigen. Denn obgleich sie, als anschauliche Vorstellung, durchweg genau bestimmt sind und auf diese Weise für Allgemeinheit durch das Unbestimmtgelassene keinen Raum geben; so sind sie doch allgemein: weil sie die bloßen Formen aller Erscheinungen sind, und als solche von allen realen Objekten, denen eine solche Form zukommt, gelten. Daher von diesen Normalanschauungen, selbst in der Geometrie, so gut als von den Begriffen, Das gelten würde, was Plato von seinen Ideen sagt, daß nämlich gar nicht zwei gleiche existiren können, weil solche nur Eine wären9. Dies würde, sage ich, auch von den Normalanschauungen in der Geometrie gelten, wären sie nicht, als allein räumliche Objekte, durch das bloße Nebeneinanderseyn, den Ort, unterschieden. Diese Bemerkung hat, nach dem Aristoteles, schon Plato selbst gemacht: eti de, parata aisthêta kai ta eidê, ta mathêmatika tôn pragmatôn einai phêsi metaxy, diapheronta tôn men aisthêtôn tô aidia kai akinêta einai, tôn de eidôn tô ta men poll' atta homoia einai, to de eidos auto hen hekaston monon (item praeter sensibilia et species, mathematica rerum ait media esse, a sensibilibus quidem differentia eo, quod perpetua et immobilia sunt, a speciebus vero eo, quod illorum quidem multa quaedam similia sunt, species vero ipsa unaquaeque sola)[151] . Metaph. I, 6, womit X, 1 zu vergleichen. Die bloße Einsicht nun, daß ein solcher Unterschied des Orts die übrige Identität nicht aufhebt, scheint mir jene neun Axiome ersetzen zu können und dem Wesen der Wissenschaft, deren Zweck es ist, das Einzelne aus dem Allgemeinen zu erkennen, angemessener zu seyn, als die Aufstellung neun verschiedener Axiome, die auf Einer Einsicht beruhen. Alsdann nämlich wird von den geometrischen Figuren gelten, was Aristoteles, Metaph. X, 3 sagt: en toutois hê isotês henotês (in illis aequalitas unitas est).
Von den Normalanschauungen in der Zeit aber, den Zahlen, gilt sogar kein solcher Unterschied des Nebeneinanderseyns, sondern schlechthin, wie von den Begriffen, die identitas indiscernibilium, und es giebt nur Eine Fünf und nur Eine Sieben. Auch hier ließe sich ein Grund dafür finden, daß 7 + 5 = 12 nicht, wie Herder in der Metakritik meint, ein identischer, sondern wie Kant so tiefsinnig entdeckt hat, ein synthetischer Satz a priori ist, der auf reiner Anschauung beruht. 12 = 12 ist ein identischer Satz.
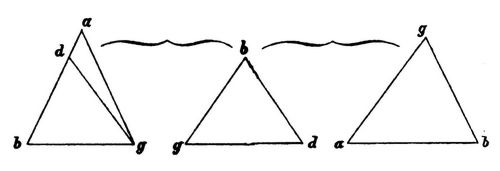
Auf die Anschauung beruft man also in der Geometrie sich eigentlich nur bei den Axiomen. Alle übrigen Lehrsätze werden demonstrirt, d.h. man giebt einen Erkenntnißgrund des Lehrsatzes an, welcher Jeden zwingt denselben als wahr anzunehmen: also man weist die logische, nicht die transscendentale Wahrheit des Lehrsatzes nach. (§§ 30 und 32.) Diese aber, welche im Grund des Seyns und nicht in dem des Erkennens liegt, leuchtet nie ein, als nur mittelst der Anschauung. Daher kommt es, daß man nach so einer geometrischen Demonstration zwar die Überzeugung hat, daß der demonstrirte Satz wahr sei, aber keineswegs einsieht, warum was er behauptet so ist, wie es ist: d.h. man hat den Seynsgrund nicht, sondern gewöhnlich ist vielmehr erst jetzt ein Verlangen nach diesem entstanden. Denn der Beweis durch Aufweisung des Erkenntnißgrundes wirkt bloß Überführung (convictio), nicht Einsicht (cognitio): er wäre deswegen[152] vielleicht richtiger elenchus, als demonstratio zu nennen. Daher kommt es, daß er gewöhnlich ein unangenehmes Gefühl hinterläßt, wie es der bemerkte Mangel an Einsicht überall giebt, und hier wird der Mangel der Erkenntniß, warum etwas so sei, erst fühlbar durch die gegebene Gewißheit, daß es so sei. Die Empfindung dabei hat Ähnlichkeit mit der, die es uns giebt, wenn man uns etwas aus der Tasche, oder in die Tasche, gespielt hat, und wir nicht begreifen wie. Der, wie es in solchen Demonstrationen geschieht, ohne den Grund des Seyns gegebene Erkenntnißgrund ist manchen Lehren der Physik analog, die das Phänomen darlegen, ohne die Ursache angeben zu können, wie z.B. der Leidenfrostische Versuch, sofern er auch im Platinatiegel gelingt. Hingegen gewährt der durch Anschauung erkannte Seynsgrund eines geometrischen Satzes Befriedigung, wie jede gewonnene Erkenntniß. Hat man diesen, so stützt sich die Überzeugung von der Wahrheit des Satzes allein auf ihn, keineswegs mehr auf den durch Demonstration gegebenen Erkenntnißgrund. Z.B. den 6. Satz des ersten Buchs Euklids: »Wenn in einem Dreieck zwei Winkel gleich sind, sind auch die ihnen gegenüberliegenden Seiten gleich« beweist Euklid so:
Das Dreieck sei a b g, worin der Winkel a b g dem Winkel a g b gleich ist; so behaupte ich, daß auch die Seite a g der Seite a b gleich ist.
Denn ist die Seite a g der Seite a b ungleich, so ist eine davon größer, a b sei größer. Man schneide von der größern a b das Stück d b ab, das der kleinern a g gleich ist, und ziehe d g. Weil nun (in den Dreiecken d b g, a b g) d b gleich a g und b g beiden gemeinschaftlich ist, so sind die zwei Seiten d b und b g den zwei Seiten a g und g b gleich, jede einzeln genommen, der Winkel d b g dem Winkel a g b, und die Grundlinie d g der Grundlinie a b, und das Dreieck a b g dem Dreieck d g b, das größere dem kleineren, welches ungereimt ist. a b ist also a g nicht ungleich, folglich gleich.
In diesem Beweis haben wir nun einen Erkenntnißgrund der Wahrheit des Lehrsatzes. Wer gründet aber seine Überzeugung von jener geometrischen Wahrheit auf diesen Beweis? und nicht vielmehr auf den durch Anschauung erkannten Seynsgrund, vermöge welches, (durch eine Nothwendigkeit die sich weiter nicht demonstriren, sondern nur anschauen läßt,) wenn von den beiden Endpunkten einer Linie sich zwei andere gleich tief gegen[153] einander neigen, sie nur in einem Punkt, der von beiden jenen Endpunkten gleich weit entfernt ist, zusammentreffen können, indem die entstehenden zwei Winkel eigentlich nur Einer sind, der bloß durch die entgegengesetzte Lage als zwei erscheint, weshalb kein Grund vorhanden ist, aus dem die Linien näher dem Einen als dem andern Punkte sich begegnen sollten.
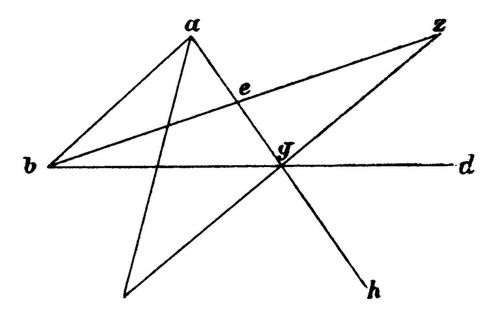
Durch Erkenntniß des Seynsgrundes sieht man die nothwendige Folge des Bedingten aus seiner Bedingung, hier der Gleichheit der Seiten aus der Gleichheit der Winkel, ein, ihre Verbindung: durch den Erkenntnißgrund aber bloß das Zusammendaseyn Beider. Ja, es ließe sich sogar behaupten, daß man durch die gewöhnliche Methode der Beweise eigentlich nur überführt werde, daß Beides in gegenwärtiger, zum Beispiel aufgestellter Figur zusammen dasei, keineswegs aber daß es immer zusammen dasei, von welcher Wahrheit (da die nothwendige Verknüpfung ja nicht gezeigt wird) man hier eine bloß auf Induktion gegründete Überzeugung erhalte, die darauf beruht, daß bei jeder Figur, die man macht, es sich so findet. Freilich ist nur bei so einfachen Lehrsätzen, wie jener sechste Euklids, der Seynsgrund so leicht in die Augen fallend: doch bin ich überzeugt, daß bei jedem, auch dem verwickeltesten Lehrsatze, derselbe aufzuweisen und die Gewißheit des Satzes auf eine solche einfache Anschauung zurückzuführen seyn muß. Auch ist sich Jeder der Nothwendigkeit eines solchen Seynsgrundes für jedes räumliche Verhältniß, so gut wie der Nothwendigkeit der Ursache für jede Veränderung, a priori bewußt. Allerdings muß derselbe, bei komplicirten Lehrsätzen, sehr schwer anzugeben seyn, und zu schwierigen geometrischen Untersuchungen ist hier nicht der Ort. Ich will daher, bloß um noch deutlicher zu machen was ich meine, einen nur wenig komplicirteren Satz, dessen Seynsgrund jedoch wenigstens nicht sogleich in die Augen fällt, auf selbigen zurückzuführen suchen. Ich gehe zehn Lehrsätze weiter, zum sechszehnten, »In jedem Dreieck, dessen eine Seite verlängert worden, ist der äußere Winkel größer, als jeder der beiden gegenüberstehenden innern.« Euklids Beweis ist folgender:
Das Dreieck sei a b g: man verlängere die Seite b g nach d, und ich behaupte, daß der äußere Winkel a g d größer sei, als jeder der beiden innern gegenüberstehenden. – Man halbire die Seite a g bei e, ziehe b e, verlängere sie bis z und mache e z[154] gleich e b, verbinde z g und verlängere a g bis h. – Da nun a e gleich e g und b e gleich e z ist, so sind die zwei Seiten a e und e b gleich den zwei Seiten g e und e z, jede einzeln genommen, und der Winkel a e b gleich dem Winkel z e g : denn es sind Scheitelwinkel. Mithin ist die Grundlinie a b gleich der Grundlinie z g und das Dreieck a b e ist gleich dem Dreieck z e g und die übrigen Winkel den übrigen Winkeln, folglich auch der Winkel b a e dem Winkel e g z. Es ist aber e g d größer als e g z, folglich ist auch der Winkel a g d größer als der Winkel b a e. – Halbiret man auch b g, so wird auf ähnliche Art bewiesen, daß auch der Winkel b g h, d.i. sein Scheitelwinkel a g d größer sei als a b g.
Ich würde den selben Satz folgendermaaßen beweisen:
Damit Winkel b a g nur gleich komme, geschweige übertreffe, Winkel a g d, müßte (denn das eben heißt Gleichheit der Winkel) die Linie b a auf g a in der selben Richtung liegen wie b d, d.h. mit b d parallel seyn, d.h. nie mit b d zusammentreffen: sie muß aber (Seynsgrund), um ein Dreieck zu bilden, auf b d treffen, also das Gegentheil dessen thun, was erfordert wäre, damit Winkel b a g nur die Größe von a g d erreichte.
Damit Winkel a b g nur gleich komme, geschweige übertreffe, Winkel a g d, müßte (denn das eben heißt Gleichheit der Winkel) die Linie b a in der selben Richtung auf b d liegen wie a g, d.h. mit a g parallel seyn, d.h. nie mit a g zusammentreffen: sie muß aber, um ein Dreieck zu bilden, auf a g treffen, also das Gegentheil thun von dem, was erfordert wäre, damit Winkel a b g nur die Größe von a g d erreichte.
Durch alles Dieses habe ich keineswegs eine neue Methode mathematischer Demonstrationen vorschlagen, auch eben so wenig meinen Beweis an die Stelle des Euklidischen setzen wollen, als wohin er, seiner ganzen Natur nach und auch schon weil er den Begriff von Parallellinien voraussetzt, der im Euklid erst später vorkommt, nicht paßt; sondern ich habe nur zeigen wollen, was Seynsgrund sei und wie er sich vom Erkenntnißgrunde unterscheide, indem dieser bloß convictio wirkt, welche etwas ganz Anderes ist, als Einsicht in den Seynsgrund. Daß man aber in der Geometrie nur strebt convictio zu wirken, welche, wie gesagt, einen unangenehmen Eindruck macht, nicht[155] aber Einsicht in den Grund des Seyns, die, wie jede Einsicht, befriedigt und erfreut; Dies möchte nebst Anderm ein Grund seyn, warum manche sonst vortreffliche Köpfe Abneigung gegen die Mathematik haben.
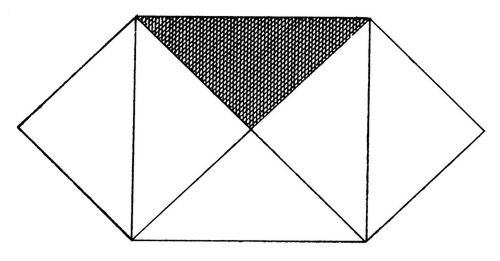
Ich kann mich nicht entbrechen, nochmals die, schon an einem andern Orte gegebene Figur herzusetzen (Fig. 6), deren bloßer Anblick, ohne alles Gerede, von der Wahrheit des Pythagorischen Lehrsatzes zwanzig Mal mehr Überzeugung giebt, als der Euklidische Mausefallenbeweis. Der für dieses Kapitel sich interessirende Leser findet den Gegenstand desselben weiter ausgeführt in der »Welt als Wille und Vorstellung«, Bd. I, § 15, und Bd. 2, Kap. 13.[156]
| 9 | Die Platonischen Ideen lassen sich allenfalls beschreiben als Normalanschauungen, die nicht nur, wie die mathematischen, für das Formale, sondern auch für das Materiale der vollständigen Vorstellungen gültig wären: also vollständige Vorstellungen, die, als solche, durchgängig bestimmt wären, und doch zugleich, wie die Begriffe) Vieles unter sich befaßten; d.h. nach meiner § 28 gegebenen Erklärung, Repräsentanten der Begriffe, die ihnen aber völlig adäquat wären. |
|
Ausgewählte Ausgaben von
Ueber die vierfache Wurzel des Satzes vom zureichenden Grunde
|
Buchempfehlung
Diderot, Denis
Die geschwätzigen Kleinode oder die Verräter. (Les Bijoux indiscrets)
Die frivole Erzählung schildert die skandalösen Bekenntnisse der Damen am Hofe des gelangweilten Sultans Mangogul, der sie mit seinem Zauberring zur unfreiwilligen Preisgabe ihrer Liebesabenteuer nötigt.
180 Seiten, 9.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Große Erzählungen der Spätromantik
Im nach dem Wiener Kongress neugeordneten Europa entsteht seit 1815 große Literatur der Sehnsucht und der Melancholie. Die Schattenseiten der menschlichen Seele, Leidenschaft und die Hinwendung zum Religiösen sind die Themen der Spätromantik. Michael Holzinger hat elf große Erzählungen dieser Zeit zu diesem Leseband zusammengefasst.
- Clemens Brentano Die drei Nüsse
- Clemens Brentano Geschichte vom braven Kasperl und dem schönen Annerl
- E. T. A. Hoffmann Das steinerne Herz
- Joseph von Eichendorff Das Marmorbild
- Ludwig Achim von Arnim Die Majoratsherren
- E. T. A. Hoffmann Das Fräulein von Scuderi
- Ludwig Tieck Die Gemälde
- Wilhelm Hauff Phantasien im Bremer Ratskeller
- Wilhelm Hauff Jud Süss
- Joseph von Eichendorff Viel Lärmen um Nichts
- Joseph von Eichendorff Die Glücksritter
430 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum