|
Raum und Geometrie vom Standpunkt der Naturforschung.526
[389] 1. Die Raumanschauung des Menschen wurzelt in dessen physiologischer Konstitution. Die geometrischen Begriffe entwickeln sich durch Idealisierung physikalischer Raumerfahrungen. Das geometrische System endlich wird durch die logische Ordnung des gewonnenen begrifflichen Stoffes geschaffen. Alle drei Momente haben in der heutigen Geometrie deutlich ihre Spuren ausgeprägt. Erkenntnistheoretische Fragen über Raum und Geometrie gehen also den Physiologen und Psychologen, den Physiker, Mathematiker, den Philosophen und Logiker an, und können nur durch Beachtung der sehr verschiedenen sich hier darbietenden Gesichtspunkte allmählich ihrer Lösung zugeführt werden.
Wenn wir in früher Jugend zu vollem Bewußtsein erwacht sind, finden wir uns bereits im Besitze der Vorstellung eines uns umgebenden, unsern Leib mit umfassenden Raumes, in welchem verschiedene Körper teils sich verändernd, teils in gleichbleibender Größe und Gestalt sich bewegen. Wie wir zu dieser Vorstellung gelangt sind, vermögen wir nicht anzugeben. Nur die genaue Analyse absichtlich und planmäßig angestellter[389] Experimente läßt uns erraten, daß hierbei schon angeborene Eigentümlichkeiten des Leibes und einfache rohe physikalische Erfahrungen zusammengewirkt haben.
Ein Gesichts- oder Tastobjekt kennzeichnet sich neben der Sinnesempfindungsqualität (rot, rauh, kühl u.s.w.) auch noch durch seine Ortsqualität (rechts, oben, vorn u.s.w.). Die Sinnesqualität kann dieselbe bleiben, während die Ortsqualität sich kontinuierlich ändert, d.h.: dasselbe sinnliche Objekt kann sich im Raume bewegen. Wenn derartige Vorgänge durch physikalisch-physiologische Umstände oft ausgelöst werden, so wiederholen sich bei der größten Mannigfaltigkeit der zufälligen Sinnesqualitäten immer wieder dieselben Reihen der Ortsqualitäten, so daß die letzteren bald als ein festes bleibendes Schema oder Register erscheinen, in welches die oben gegebenen Sinnesqualitäten eingeordnet werden. Obgleich nun Sinnes- und Ortsqualitäten nur miteinander erregt werden und nur miteinander auftreten können, so entsteht so doch leicht der Eindruck, als ob das System der geläufigeren Ortsqualitäten vor den Sinnesqualitäten gegeben wäre.
2. Ausgedehnte Gesichts- und Tastobjekte bestehen aus mehr oder weniger unterscheidbaren Sinnesqualitäten, welche mit benachbarten unterscheidbaren, stetig abgestuften Ortsqualitäten verbunden sind. Bewegen sich solche Objekte, namentlich im Bereiche unserer Hände, so nehmen wir ein Schrumpfen oder Schwellen (im ganzen oder in deren Teilen), oder ein Gleichbleiben derselben wahr, d.h. die Kontraste der Grenz-Ortsqualitäten verändern sich oder bleiben konstant. Im letzteren Falle nennen wir die Objekte starr. Durch die Erkenntnis eines sich Gleichbleibenden, trotz der räumlichen Verschiebung, treten die verschiedenen Teile unserer Raumanschauung in das Verhältnis der Vergleichbarkeit, zunächst im physiologischen Sinne. Durch die Vergleichung der verschiedenen Körper untereinander, durch die Einführung des physikalischen Maßes, wird die Vergleichbarkeit zu einer genaueren quantitativen, welche zugleich die Schranken des Individuums durchbricht. So treten an die Stelle der individuellen, nicht übertragbaren Raumanschauung die allgemein für alle Menschen gültigen Begriffe der Geometrie. Jeder hat seinen besonderen Anschauungsraum; der geometrische Raum ist gemeinsam. Zwischen dem Anschauungsraum[390] und dem auch physikalische Erfahrungen enthaltenden metrischen Raum müssen wir scharf unterscheiden.
3. Das Bedürfnis nach einer tiefgehenden erkenntnistheoretischen Aufklärung der Grundlagen der Geometrie hat um die Mitte des abgelaufenen Jahrhunderts Riemann527 dazu geführt, die Frage nach der Natur des Raumes zu stellen, nachdem schon vorher durch Gauß, Lobatschefskij und die beiden Bolyai die Aufmerksamkeit auf die empirisch-hypothetische Bedeutung gewisser Grundannahmen der Geometrie gelenkt worden war. Wenn Riemann den Raum als einen besonderen Fall einer mehrfach ausgedehnten »Größe« bezeichnet, so denkt er wohl an ein geometrisches Gebilde, das etwa auch als den ganzen Raum erfüllend vorgestellt werden könnte, z.B. ein Descartessches Koordinatensystem. Riemann spricht es ferner aus, »daß die Sätze der Geometrie sich nicht aus allgemeinen Größenbegriffen ableiten lassen, sondern daß diejenigen Eigenschaften, durch welche sich der Raum von anderen denkbaren dreifach ausgedehnten Größen unterscheidet, nur aus der Erfahrung entnommen werden können«... »Diese Tatsachen sind wie alle Tatsachen nicht notwendig, sondern nur von empirischer Gewißheit, sie sind Hypothesen.« Wie die Grundannahmen jeder Naturwissenschaft, könnte man sagen, so sind auch die Grundannahmen der Geometrie, zu welchen die Erfahrung hingeleitet hat, Idealisierungen dieser Erfahrung. Mit seiner naturwissenschaftlichen Auffassung der Geometrie steht Riemann auf dem Boden seines Lehrers Gauß. Gauß spricht gelegentlich die Überzeugung aus, »daß wir die Geometrie nicht vollständig a priori begründen können«...528 »Wir müssen in Demut zugeben, daß, wenn die Zahl bloß unseres Geistes Produkt ist, der Raum auch außer unserm Geiste eine Realität hat, der wir a priori ihre Gesetze nicht vollständig vorschreiben können.«529
4. Jeder Forscher hat es erfahren, daß die Erkenntnis eines zu[391] untersuchenden Objektes durch die Vergleichung mit verwandten Objekten wesentlich gefördert wird. Wie natürlich sieht sich also Riemann nach Dingen um, welche eine Analogie zum Raum darbieten. Der geometrische Raum wird von ihm als eine dreifach ausgedehnte, stetige Mannigfaltigkeit bezeichnet, als deren Elemente die durch je drei Koordinatenwerte bestimmten Punkte anzusehen sind. Er findet, »daß die Orte der Sinnesgegenstände und die Farben wohl die einzigen Begriffe (?) sind, deren Bestimmungsweisen eine mehrfache ausgedehnte Mannigfaltigkeit bilden«. Dieser Analogie wurden von anderen noch neue hinzugefügt und weiter verfolgt, doch, wie ich glaube, nicht immer in glücklicher Weise.530
5. Vergleichen wir zunächst die Raumempfindung mit der Farbenempfindung, so sehen wir, daß den stetigen Reihen: oben – unten, rechts – links, nahe – fern die drei Empfindungsreihen der Farben: schwarz – weiß, rot – grün, gelb – blau entsprechen. Das System der empfundenen (angeschauten) Orte ist ebenso eine dreifache stetige Mannigfaltigkeit, wie das System der Farbenempfindungen. Die Einwendung, welche gegen diese Analogie vorgebracht worden ist, daß nämlich im ersteren Falle die drei Variationen (Dimensionen) homogen (gleichartig) und miteinander vertauschbar sind, im zweiten Falle aber heterogen und nicht vertauschbar, trifft nicht zu, wenn man die Raumempfindung mit der Farbenempfindung vergleicht. Denn psycho-physiologisch kann rechts – links ebensowenig mit oben – unten vertauscht werden, als rot – grün mit schwarz – weiß. Nur wenn man den geometrischen Raum mit dem System der Farben vergleicht, gewinnt[392] die Einwendung einen Anschein von Berechtigung. Allein zur vollen Analogie des Anschauungsraumes und des Systems der Farbenempfindung fehlt noch manches. Während nahe gleiche Entfernungen im Anschauungsraum unmittelbar als solche erkannt werden, können wir über die Differenz der Farben nichts derartiges aussagen, und es fehlt daher dem letzteren Gebiete die physiologische Vergleichbarkeit seiner Teile untereinander. Wenn es auch keiner Schwierigkeit unterliegt, durch Zuziehung physikalischer Erfahrungen jede Farbe des Systems durch drei Zahlen zu bezeichnen, wie die Orte im geometrischen Raum, und so ein dem letzteren ähnliches metrisches System zu schaffen, so wird sich doch schwerlich etwas finden, das der Distanz oder dem Volumen entspricht, und das für das Farbensystem eine analoge physikalische Bedeutung hat.
6. Analogien haben immer etwas Willkürliches, da es auf die Übereinstimmungen ankommt, auf die man die Aufmerksamkeit richtet. Man wird aber wohl allgemein die Analogie zwischen Raum und Zeit zugeben, und zwar sowohl wenn man die Worte im physiologischen, als auch wenn man sie im physikalischen Sinne nimmt. In beiden Bedeutungen ist ersterer eine dreifache, letztere eine einfache stetige Mannigfaltigkeit. Ein durch die Umstände genau bestimmter physikalischer Vorgang von mäßiger, nicht zu langer oder kurzer Dauer erscheint uns jetzt und zu einer beliebigen andern Zeit unmittelbar physiologisch von gleicher Dauer. Physikalische Vorgänge, die sich irgendwann zeitlich decken, decken sich auch zeitlich zu jeder andern Zeit. Es gibt also zeitliche Kongruenz, so wie es räumliche Kongruenz gibt. Es existiert also ein unveränderliches physikalisches Zeitobjekt, so wie es ein unveränderliches physikalisches Raumobjekt (den starren Körper) gibt. Es gibt nicht nur räumliche, sondern auch zeitliche Substanzialität. Leibliche Vorgänge: Puls und Atmung verwendete noch Galilei zur Zeitschätzung, so wie man ehemals Hände und Füße zur Raumschätzung benützte.
7. Der dreifachen Mannigfaltigkeit der Raumempfindungen ist auch analog die einfache Mannigfaltigkeit der Tonempfindungen.531[393] Die Vergleichbarkeit der verschiedenen Teile des Systems der Tonempfindungen ist durch die unmittelbare Empfindung des musikalischen Intervalls gegeben. Man erhält ein dem geometrischen Raum entsprechendes metrisches System am einfachsten, indem man die Tonhöhe durch den Logarithmus der Schwingungszahl charakterisiert. Dem konstanten musikalischen Intervall entspricht hier der Ausdruck
log n'/n = log n'-log n = logτ – logτ' = konst.,
wobei n', n die Schwingungszahl, τ', τ die Schwingungsdauer des höheren, bezw. des tieferen Tones bedeutet. Der Unterschied der Logarithmen vertritt hier die bei der Verschiebung konstant bleibende Länge. Das unveränderliche substanzielle physikalische Objekt, welches wir als Intervall empfinden, ist für das Ohr zeitlich bestimmt, während das analoge Objekt für den Gesichts- und Tastsinn räumlich bestimmt ist. Das Raummaß erscheint uns nur deshalb einfacher, weil wir die Länge selbst, die für den Sinn unveränderlich bleibt, auch als Grundmaß der Geometrie wählen, während wir zu dem Maße im Gebiet der Töne erst auf einem langen physikalischen Umwege gelangt sind.
8. Es ist nun notwendig, außer den Übereinstimmungen der in Analogie gesetzten Gebilde auch deren Unterschiede zu betonen. Fassen wir Zeit und Raum als Empfindungsmannigfaltigkeiten auf, so sind die Objekte, deren Bewegung durch Änderung der Zeit- und Ortsqualitäten sich bemerklich macht, durch andere Empfindungsqualitäten: Farben, Tastempfindungen, Töne u.s.w. gekennzeichnet. Wird aber z.B. das System der Tonempfindungen als analog dem optischen Anschauungsraum angesehen, so ergibt sich die Sonderbarkeit, daß in ersterem Gebiet die Ortsqualitäten allein ohne andere den Objekten entsprechende Empfindungsqualitäten auftreten, so als ob man einen Ort oder eine bestimmte Bewegung sehen könnte, ohne ein Objekt zu sehen, welches diesen Ort einnimmt, oder diese Bewegung ausführt. Stellt man sich die Ortsqualitäten als Organempfindungen vor, welche nur mit den Sinnesqualitäten532 erregt werden können, so[394] wird man die genannte Analogie nicht besonders einladend finden. Für den Mannigfaltigkeitsmathematiker liegt im wesentlichen derselbe Fall vor, ob ein Objekt von bestimmter Farbe sich stetig im optischen Raume bewegt, oder ob ein Gegenstand von fest bestimmtem Ort in stetiger Veränderung die Mannigfaltigkeit der Farben durchläuft. Für den Physiologen und Psychologen sind die beiden Fälle sehr verschieden, nicht nur nach dem oben Bemerkten, sondern noch durch einen besonderen Umstand. Das System der Ortsqualitäten ist uns sehr geläufig, während wir uns ein System der Farbenempfindung nur mühsam und künstlich auf Grund wissenschaftlicher Studien vergegenwärtigen. Die Farbe erscheint uns als ein herausgerissenes Glied einer Mannigfaltigkeit, deren Ordnung uns nicht geläufig ist.
9. Die hier mit dem Raum in Analogie gesetzten Mannigfaltigkeiten sind wie das Farbensystem ebenfalls dreifach, oder bieten eine geringere Zahl von Variationen dar. Der Raum selbst enthält in sich Flächen als zweifache, Linien als einfache Mannigfaltigkeiten, zu welchen der Mathematiker in seiner verallgemeinernden Sprache noch die Punkte als 0-fache zählen könnte. Es ist aber auch keine Schwierigkeit die analytische Mechanik, wie es geschehen ist, als analytische Geometrie von 4 Dimensionen – die Zeit als vierte betrachtet – aufzufassen. Überhaupt legen die in Bezug auf die Koordinaten konformen Gleichungen der analytischen Geometrie dem Mathematiker den Gedanken nahe, derartige Betrachtungen auf eine beliebige größere Zahl von Dimensionen auszudehnen. Auch die Physik könnte ein ausgedehntes materielles Kontinuum, von dem jedem Punkt eine Temperatur, ein magnetisches, elektrisches, Gravitationspotential u.s.w. zugeschrieben würde, als ein Stück, einen Ausschnitt einer mehrfachen Mannigfaltigkeit betrachten. Die Operation mit solchen symbolischen Darstellungen kann, wie die Geschichte der Wissenschaft lehrt, keineswegs als ganz unfruchtbar angesehen werden. Symbole, welche anfänglich gar keinen Sinn zu haben schienen, gewannen, sozusagen bei den Gedankenexperimenten mit denselben, allmählich eine klare und präcise Bedeutung. Man denke z.B. an die negativen, gebrochenen und variablen Potenzexponenten und ähnliche Fälle, in welchen sich auf diesem Wege wichtige und wesentliche Begriffserweiterungen[395] ergaben, die sonst ganz ausgeblieben wären, oder sich erst viel später eingestellt hätten. Man denke an die sogenannten Imaginären, mit welchen man lange rechnete, und sogar wichtige Resultate gewann, bevor man im stande war, denselben einen genau bestimmten und sogar auch anschaulichen Sinn beizulegen. Die symbolische Darstellung hat aber allerdings den Nachteil, daß man den dargestellten Gegenstand gar zu leicht ganz aus den Augen verliert, und mit Zeichen operiert, welchen gelegentlich auch gar kein Objekt entspricht.533
10. Zu der Riemannschen Vorstellung seiner n-fachen stetigen Mannigfaltigkeit kann man sich in der Tat leicht erheben und es gelingt sogar, Teile einer solchen Mannigfaltigkeit zu realisieren und anschaulich zu machen. Es seien a[1], a[2], a[3], a[4] ... a[n+1] beliebige Elemente (Empfindungsqualitäten, Stoffe u.s.w.). Wenn wir uns diese Elemente in allen möglichen Verhältnissen gemischt vorstellen, so ist jede einzelne Mischung durch den Ausdruck dargestellt[396]
α[1]a[1] + α[2]a[2] + α[3]a[3] + ... α[n+1]a[n+1],
wobei die Koeffizienten α der Gleichung genügen
α[1] + α[2] + α[3] + .... α[n+1] = 1.
Da hiernach n der Koeffizienten α beliebig gewählt werden können, so stellt die Gesamtheit der Mischungen aus n+1 Elementen eine n-fache stetige Mannigfaltigkeit dar.534 Als Koordinaten eines Punktes, Elementes dieser Mannigfaltigkeit kann man Ausdrücke von der Form α[m]/α[1] oder F(α[m]/α[1]), z.B. log(α[m]/α[1]) ansehen. Aber bei der Wahl der Definition der Entfernung, oder anderer den geometrischen analoger Begriffe wird man recht willkürlich vorgehen müssen, wenn nicht Erfahrungen über die betreffende Mannigfaltigkeit lehren, daß bestimmte metrische Begriffe eine reelle Bedeutung haben, und deshalb zu bevorzugen sind, wie dies für den geometrischen Raum mit der aus der Volumenbeständigkeit der Körper folgenden Definition535 für das Entfernungselement ds2 = dx2 + dy2 + dz2, und für die Tonempfindungen mit dem erwähnten logarithmischen Ausdruck der Fall ist. In den meisten Fällen einer solchen künstlichen Konstruktion werden solche Anhaltspunkte fehlen, und die ganze Betrachtung wird demnach eine müßige sein. Die Analogie zum Raum verliert dadurch an Vollständigkeit, Fruchtbarkeit und fördernder Kraft.
11. Noch in einer anderen Richtung hat Riemann Gedanken von Gauß weitergesponnen, anknüpfend an die Untersuchungen des letzteren über die krummen Flächen. Das Gaußsche Krümmungsmaß536 einer Fläche in einem Punkte ist gegeben durch den Ausdruck k = dσ/ds, wobei ds ein Element der Fläche, dσ das Oberflächenelement der Einheitskugel bedeutet, dessen Grenzradien den Grenznormalen des Elementes ds parallel sind. Dieses Krümmungsmaß kann auch in der Form ausgedrückt werden[397] k = 1/ρ1 · ρ2, wobei ρ1, ρ2 die Hauptkrümmungsradien der Fläche in dem betreffenden Punkt bedeuten. Von besonderem Interesse sind die Flächen, deren Krümmungsmaß für alle Punkte denselben Wert hat, die Flächen von konstantem Krümmungsmaß. Denkt man sich die Flächen als unendlich dünne nicht ausdehnbare aber biegsame Körper, so können Flächen von gleichem Krümmungsmaß durch Biegung zur Deckung gebracht werden, wie man z.B. ein ebenes Blatt Papier um den Mantel eines Zylinders oder Kegels wickeln, nicht aber mit einer Kugelfläche zur Deckung bringen kann. Bei dieser Deformation, ja selbst bei beliebiger Zerknitterung, bleiben die Maßverhältnisse in der Fläche gezeichneter Figuren mit ihren Längen und Winkeln unverändert, sobald man nur messend aus den zwei Dimensionen der Fläche nicht herausgeht. Umgekehrt hängt auch das Krümmungsmaß der Fläche gar nicht von deren Gestaltung nach der dritten Dimension des Raumes, sondern nur von deren inneren Maßverhältnissen ab. Riemann faßte nun den Gedanken, den Begriff des Krümmungsmaßes für Räume von drei und mehreren Dimensionen zu verallgemeinern. Demgemäß nimmt er die Möglichkeit von endlichen unbegrenzten Räumen konstanten positiven Krümmungsmaßes an, entsprechend der unbegrenzten aber endlichen zweidimensionalen Kugelfläche, während der nach unserer gewöhnlichen Vorstellung unendliche Raum der endlosen Ebene vom Krümmungsmaß Null, und ebenso eine dritte Raumspecies den Flächen von negativem Krümmungsmaß entsprechen würde. So wie die auf einer Fläche von bestimmtem konstantem Krümmungsmaß gezeichnete Figur nur auf dieser ohne Verzerrung verschoben werden kann, wie z.B. eine sphärische Figur nur auf dieser Sphäre, eine ebene Figur nur in der Ebene, so müßte das Analoge für räumliche Figuren, für starre Körper gelten. Nur in Räumen von konstantem Krümmungsmaß könnten die letzteren frei beweglich sein, wie Helmholtz537 weiter ausgeführt hat. So wie die kürzesten Linien in der Ebene unendlich, auf der Kugelfläche aber als größte Kreise von bestimmter endlicher Länge[398] und geschlossen (in sich zurücklaufend) sind, so dachte sich Riemann im dreidimensionalem Raum von positivem Krümmungsmaß die Analoga der Geraden und Ebene endlich aber unbegrenzt. Nun besteht hier eine Schwierigkeit. Hätte man den Begriff des Krümmungsmaßes für einen vierdimensionalen Raum, so wäre der Übergang auf den speziellen Fall des dreidimensionalen Raumes leicht sinngemäß auszuführen. Der Übergang von dem spezielleren auf den allgemeineren Fall schließt aber eine gewisse Willkür in sich, und wie natürlich haben hier verschiedene Forscher ungleiche Wege eingeschlagen.538 (Riemann, Kronecker.) Schon der Umstand, daß es für den eindimensionalen Raum – eine beliebige krumme Linie – ein Krümmungsmaß von der Bedeutung eines inneren Maßes gar nicht gibt, und daß das letztere erst bei zweidimensionalen Gebilden auftritt, drängt uns die Frage auf, ob und wie weit Analoges für dreidimensionale Gebilde überhaupt einen Sinn hat? Unterliegen wir hier nicht einer Illusion, indem wir mit Symbolen operieren, welchen vielleicht überhaupt nichts Wirkliches entspricht, jedenfalls nichts Anschauliches, an dem wir unsere Begriffe verifizieren und rektifizieren könnten?
So hätten wir also die höchsten und allgemeinsten Ideen über den Raum und dessen Beziehungen zu analogen Mannigfaltigkeiten gewonnen, die sich aus der Gaußschen Überzeugung von der empirischen Begründung der Geometrie ergeben haben. Die Genesis dieser Überzeugung hat aber eine zweitausendjährige Vorgeschichte, deren Hauptphänomene wir, von der gewonnenen Höhe aus, vielleicht besser überschauen werden.
12. Die naiven Menschen, welche mit dem Maßstab in der Hand die ersten geometrischen Kenntnisse erwarben, hielten sich an die einfachsten körperlichen Gebilde: die Gerade, die Ebene, den Kreis u.s.w., und untersuchten an Formen, die sich als Kombination jener einfachen Gebilde auffassen ließen, den Zusammenhang der Abmessungen. Es kann ihnen nicht entgangen sein, daß die Beweglichkeit eines Körpers beschränkt wird, wenn man einen, dann zwei Punkte desselben fixiert, und daß sie[399] endlich durch Festhalten dreier Punkte vollkommen aufgehoben wird. War die Drehung um eine Achse, um zwei Punkte, oder die Drehung um einen Punkt in der Ebene, sowie die Verschiebung bei stetigem Kontakt zweier Punkte mit einer Geraden, und eines dritten Punktes mit einer durch jene Gerade gelegten festen Ebene isoliert beobachtet, so wußte man die reine Drehung, reine Verschiebung und die aus beiden unabhängigen Bewegungen kombinierte Bewegung zu unterscheiden. Die erste Geometrie war natürlich nicht auf rein metrische Begriffe gegründet, sondern machte dem physiologischen Moment, der Anschauung, bedeutende Zugeständnisse.539 So erklärt sich das Auftreten von zwei verschiedenen Grundmaßen: (gerade) Länge und Winkel (Kreismaß). Die Gerade wurde als starrer beweglicher Körper (Maßstab), der Winkel als Drehung einer Geraden gegen eine andere (gemessen durch den hierbei beschriebenen Kreisbogen) aufgefaßt. Für die Gleichheit der durch dieselbe Drehung beschriebenen Scheitelwinkel wird gewiß niemand einen besondern Beweis verlangt haben. Auch andere Winkelsätze ergaben sich sehr einfach.
Dreht man (Fig. 22) die Gerade b, den Winkel α beschreibend, um den Schnittpunkt mit c bis zum Zusammenfallen mit dieser, hierauf um den Schnittpunkt mit a, den Winkel β beschreibend, bis zur Deckung mit dieser, so hat man b aus der Anfangslage in die Endlage a um den Winkel u in demselben Sinne gedreht. Daher der Außenwinkel u = α + β, und weil u + γ = 2R, auch α + β + γ = 2R.540[400]
Verschiebt man (Fig. 23) das starre System der in 1 sich schneidenden Geraden a, b, c in seiner Ebene bis 2, so daß die Gerade a in sich verbleibt, so ändert sich durch die reine Verschiebung kein Winkel. Die Summe der Innenwinkel des hierbei entstandenen Dreiecks 1 2 3 ist ersichtlich 2R. Dieselbe Betrachtung setzt auch die Eigenschaften der Parallelen ins Licht. Bedenken wie die, ob die successive Drehung um mehrere Punkte wirklich äquivalent ist der Drehung um einen Punkt, ob es eine reine Verschiebung überhaupt gibt – die sofort berechtigt sind, sobald man an die Stelle der (Euklidischen) Ebene eine Fläche mit von Null verschiedener Krümmung treten läßt – können bei dem freudigen naiven Finder dieser Beziehungen auf dieser Stufe natürlich nicht auftreten. Die Betrachtung der Bewegung starrer Körper, welche Euklid sorgfältig vermeidet, und die er nur verdeckt im Kongruenzprinzip einführt, ist heute noch das zweckmäßigste Mittel für den geometrischen Elementarunterricht. Am besten wird eine Einsicht Eigentum des Lernenden auf demselben Wege, auf welchem sie gefunden wurde.
13. Die gesunde naive Auffassung verschwand, und die Behandlung der Geometrie änderte sich wesentlich, sobald dieselbe Gegenstand des berufsmäßigen gelehrten Denkens wurde. Nun galt es zunächst für die eigene Übersicht das Wissen in ein System zu bringen, das unmittelbar Erkannte von dem Ableitbaren und Abgeleiteten zu sondern, den Faden der Ableitung deutlich hervorzuheben. Für den Zweck des Unterrichts wurden die einfachsten, am leichtesten zu erwerbenden Kenntnisse, welche keinem Zweifel und Widerspruch ausgesetzt schienen, an die Spitze gestellt, um das übrige darauf zu gründen. Man bemühte[401] sich, diese Ausgangssätze noch auf das Notwendigste zu reduzieren, wie wir dies alles an dem System des Euklid sehen. Bei diesem Streben jede Einsicht durch eine andere zu stützen, und nur das wenigste der unmittelbaren Erkenntnis zu überlassen, wurde die Geometrie von dem empirischen Boden, auf welchem sie entstanden war, allmählich losgelöst. Man gewöhnte sich die abgeleitete Einsicht höher zu schätzen als die unmittelbar erschaute, und verlangte schließlich Beweise für Sätze, an welchen niemand ernstlich zweifelte. So entstand – der Tradition nach zum Schutz gegen die Angriffe der Sophisten – das logisch vollendete geschlossene System Euklids. Bei dieser künstlichen Aufreihung der Sätze an einem willkürlich gewählten Faden der Ableitung wurden aber nicht nur die Wege der Forschung absichtlich verdeckt, sondern auch der vielfache organische Zusammenhang der geometrischen Lehren blieb unsichtbar.541 Das System war eher geeignet, ängstliche sterile Pedanten, als fruchtbare produktive Forscher zu erziehen. Dieser Zustand wurde nicht gebessert, als die fremde Geistesprodukte mit Vorliebe sklavisch kommentierende Scholastik die Menschen an eine sehr geringe Empfindlichkeit für die Rationalität der Grundannahmen, und dafür an desto größere Achtung für die logische Form der Ableitung gewöhnte. Die ganze Zeit nach Euklid bis auf Gauß leidet mehr oder weniger unter dieser Stimmung.[402]
14. Unter den Sätzen, auf welche Euklid sein System gründete, befand sich die sogenannte fünfte Forderung (auch als 11. Axiom bezeichnet): »2 Gerade, die von einer dritten so geschnitten werden, daß die innern an derselben Seite der Schneidenden liegenden Winkel zusammen kleiner sind als 2 Rechte, treffen genügend verlängert an eben dieser Seite zusammen.« Es gelingt Euklid leicht zu zeigen, daß 2 Gerade, die mit einer dritten Schneidenden gleiche Wechselwinkel bilden, sich nicht treffen, parallel sind. Die Umkehrung aber, daß Parallele mit jeder schneidenden Geraden gleiche Wechselwinkel bilden, muß er auf die fünfte Forderung stützen. Diese Umkehrung ist gleichbedeutend mit dem Satze, daß durch einen Punkt zu einer Geraden nur eine Parallele möglich ist. Da nun mit Hilfe dieser Umkehrung nachgewiesen wird, daß die Winkelsumme des Dreiecks 2 R ist, und da aus letzterer Behauptung erstere wieder folgt, so ist hiermit der Zusammenhang der genannten Sätze deutlich gemacht, und die fundamentale Bedeutung der fünften Forderung für die Euklidische Geometrie klargelegt.
15. Der Schnitt schwach konvergierender Geraden liegt außerhalb des Gebietes der Konstruktion und der Beobachtung. Es ist daher begreiflich, daß die durch Euklid an Strenge gewöhnten Nachfolger desselben, bei der Wichtigkeit der Aussage der fünften Forderung schon in der antiken Zeit bemüht waren, diese Aussage zu beweisen, oder durch einen unmittelbar einleuchtenden Satz zu ersetzen. Von Euklid bis auf Gauß wurden zahlreiche erfolglose Versuche unternommen, den Inhalt der fünften Forderung, aus den übrigen Euklidischen Annahmen abzuleiten. Es ist ein erhebendes Beispiel, das diese Menschen darbieten, indem sie durch Jahrhunderte lediglich im reinen Trieb nach wissenschaftlicher Aufklärung nach der Erkenntnisquelle eines Satzes suchen, an dessen Richtigkeit weder ein Theoretiker noch ein Praktiker bis auf den heutigen Tag wirklich ernstlich gezweifelt hat. Mit Spannung verfolgen wir die beharrlichen Äußerungen der ethischen Kraft des Wissenstriebes, und erfreut beobachten wir, wie die Forscher durch ihre Mißerfolge allmählich zur Erfahrung als der wahren Grundlage der Geometrie hingeleitet werden. Wir wollen uns an einigen Beispielen genügen lassen.[403]
16. Zu den Forschern, welche sich bedeutende Verdienste um die Lehre von den Parallelen erworben haben, gehört der Italiener Saccheri und der deutsche Mathematiker Lambert. Um die Art, wie beide die Frage anfassen, deutlich zu machen, bemerken wir zunächst, daß die Existenz von Rechtecken und Quadraten, die wir doch fortwährend zu beobachten glauben, ohne Hilfe der fünften Forderung nicht nachgewiesen werden kann.
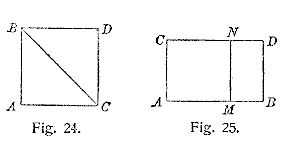
Betrachten wir z.B. zwei kongruente, gleichschenklige bei A und D rechtwinklige Dreiecke ABC und DBC (Fig. 24), welche wir mit den Hypotenusen BC aneinanderlegen, so daß das gleichseitige Viereck ABCD entsteht, so genügen die ersten 27 Sätze Euklids nicht, die Art und Größe der beiden gleichen (rechten) Winkel bei B und C zu bestimmen. Das Längenmaß und das Winkelmaß sind ja grundverschieden und nicht einfach vergleichbar, daher die ersten Sätze über den Zusammenhang der Seiten und Winkel des Dreiecks nur qualitative, daher ein quantitativer Winkelsatz, wie der Winkelsummensatz unbedingt erforderlich. Bemerken wir ferner, daß den 27 planimetrischen Sätzen analoge für die Kugelfläche und die Flächen konstanter negativer Krümmung aufgestellt werden können, und daß dann die analoge Konstruktion die Winkel bei B und C stumpf, bezw. spitz ergibt.
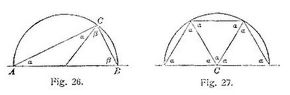
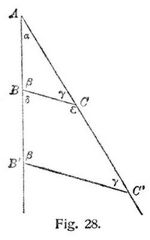
17. Das Hauptverdienst Saccheris542 liegt nun in der Form seiner Problemstellung. Steckt die fünfte Forderung schon in den übrigen Voraussetzungen Euklids, so muß es auch ohne dieselbe gelingen zu beweisen, daß in dem Viereck ABCD (Fig. 25) mit den rechten Winkeln in A und B, und bei AC = BD, die Winkel in C, D rechte sind. Dagegen muß in diesem Falle[404] die Annahme, C und D seien stumpf oder spitz zu Widersprüchen führen. Saccheri versucht also aus den Hypothesen des rechten stumpfen oder spitzen Winkels Folgerungen zu ziehen. Es gelingt ihm zu zeigen, daß jede dieser Hypothesen in allen Fällen gilt, wenn sie nur in einem Falle richtig ist. Durch irgend ein Dreieck, dessen Winkelsumme gleich 2R, größer oder kleiner ist, wird die Gültigkeit der Hypothese des rechten, stumpfen oder spitzen Winkels allgemein nachgewiesen. Bemerkenswert ist, daß Saccheri schon auf physikalisch-geometrische Versuche hinweist, welche die Hypothese des rechten Winkels stützen. Verbindet (Fig. 25) eine Gerade CD die Endpunkte der auf einer Geraden AB errichteten gleichen Lote AC und BD, und ist das von einem beliebigen Punkte N der ersteren Geraden auf AB gefällte Lot NM = CA = DB, so ist die Richtigkeit der Hypothese des rechten Winkels nachgewiesen. Daß die Linie gleichen Abstandes von einer Geraden wieder eine Gerade sei, hält Saccheri mit Recht nicht für selbstverständlich. Man denke nur an den Parallelkreis zum größten Kreise der Kugel, welcher auf der Kugel keine Kürzeste darstellt, und dessen beide Seiten sich nicht decken. Andere experimentelle Beweise für die Richtigkeit der Hypothese des rechten Winkels sind noch folgende. Erweist sich der Winkel im Halbkreise (Fig. 26) als ein rechter, α + β = R, so ist auch 2α + 2β = 2R die Winkelsumme in dem Dreieck ABC. Wenn der Radius im Halbkreise dreimal aufgetragen wird, und die Verbindungsgerade des ersten und vierten Endpunktes durch den Mittelpunkt geht, so ist bei C (Fig. 27) 3α = 2R, und demnach hat jedes der drei Dreiecke die Winkelsumme 2R. Die Existenz ungleich großer gleichwinkliger (ähnlicher) Dreiecke ist ebenfalls ein experimenteller Beweis. Denn wenn (Fig. 28) die Winkel bei B und C ergeben β + δ + γ + ε = 4R, so ist 4R auch die Winkelsumme des Vierecks[405] BCB'C'. Schon Wallis543 hatte 1663 den Beweis der fünften Forderung auf die Voraussetzung der Existenz ähnlicher Dreiecke gegründet, und ein moderner Geometer, Delboeuf, leitete aus der Annahme der Ähnlichkeit die ganze Euklidische Geometrie ab.
Die Hypothese des stumpfen Winkels meinte Saccheri leicht widerlegen zu können. Die Hypothese des spitzen Winkels bereitete ihm aber Schwierigkeiten, und trieb ihn im Suchen nach den erwarteten Widersprüchen zu weiter und weiter gehenden Folgerungen, die später Lobatschefskij und Bolyai auf ihren Wegen wiederfanden. Schließlich glaubt er letztere Hypothese als mit der Natur der Geraden unverträglich auf geben zu müssen, denn sie führt zur Annahme von verschiedenen Geraden, welche im Unendlichen zusammenfallen, also dort ein gemeinsames Lot haben. Saccheri hat die spätere Aufklärungsarbeit wesentlich vorbereitet und gefördert, zeigte aber den hergebrachten Ansichten gegenüber noch eine gewisse Befangenheit.
18. Die Arbeit Lamberts 1766544 ist in der Methode jener Saccheris verwandt, geht aber in den Folgerungen etwas weiter und bekundet einen noch freieren Blick. Lambert geht von der Betrachtung eines Viereckes mit drei rechten Winkeln aus, und untersucht die Folgen, die sich ergeben, je nachdem man den vierten Winkel als einen rechten, stumpfen oder spitzen voraussetzt. Die Ähnlichkeit der Figuren findet er mit der zweiten und dritten Annahme unverträglich. Den Fall des stumpfen Winkels, an welchen eine 2R überschreitende Winkelsumme des Dreiecks geknüpft ist, findet er in der Geometrie der Kugelfläche verwirklicht, in welcher die Schwierigkeit der Parallellinien ganz wegfällt. Dies führt ihn auf die Vermutung, daß der Fall des spitzen Winkels, mit einer Dreieckswinkelsumme[406] unter 2R, auf einer imaginären Kugel verwirklicht sein möchte. Die Abweichung der Winkelsumme von 2R ist in beiden Fällen der Dreiecksfläche proportional, wie sich durch passende Teilung größerer Dreiecke in kleinere, welche mit der Verkleinerung der Winkelsumme 2R beliebig nahe kommen, nachweisen läßt. Hiermit nähert sich Lambert bedeutend dem Standpunkt der modernen Geometer. Eine Kugel mit imaginärem Radius r√-1 ist zwar kein anschauliches geometrisches Gebilde, ist aber analytisch eine Fläche von negativem konstantem Gaußschem Krümmungsmaß. Man sieht an diesem Fall wieder, wie auch das Experimentieren mit Symbolen eine Untersuchung auf den richtigen Weg weisen kann, in einem Stadium, wo andere Anhaltspunkte eben noch ganz fehlen, und wo jedes Mittel, das fördern kann, geschätzt werden muß.545 Scheint doch auch Gauß an die imaginäre Kugel gedacht zu haben, wie aus seiner Formel für den Kreisumfang (Brief an Schumacher vom 12. Juli 1831) hervorgeht. Dennoch glaubt auch Lambert dem Beweis der fünften Forderung so nahe gekommen zu sein, daß das Fehlende leicht zu ergänzen wäre.
19. Wenden wir uns nun zu dem Forscher, dessen Ansichten die radikalste Wendung in Bezug auf die Auffassung der Geometrie bedeuten, der aber dieselben leider nur in kurzen mündlichen oder brieflichen Bemerkungen mitgeteilt hat. »Die Geometrie betrachtete Gauß nur als ein konsequentes Gebäude, nachdem die Parallelentheorie als Axiom an der Spitze zugegeben sei; er sei indes zur Überzeugung gelangt, daß dieser Satz nicht bewiesen werden könne, doch wisse man aus der Erfahrung, z.B. aus den Winkeln des Dreieckes: Brocken, Hohenhagen, Inselsberg, daß er näherungsweise richtig sei. Wolle man dagegen das genannte Axiom nicht zugeben, so folge daraus eine andere, ganz selbständige Geometrie, die er gelegentlich einmal verfolgt und mit dem Namen Antieuklidische Geometrie bezeichnet habe.« So dachte Gauß nach dem Bericht von Sartorius von Waltershausen.546 O. Stolz hat hieran anknüpfend versucht, in einer kleinen sehr lehrreichen[407] Abhandlung547 die Hauptsätze der Euklidischen Geometrie abzuleiten, ohne das Gebiet der beobachtbaren Tatsachen zu verlassen. Aus derselben soll hier das Wichtigste mitgeteilt werden. Es sei also (Fig. 29) ein großes Dreieck ABC mit der Winkelsumme 2R gegeben. Wir ziehen die Senkrechte AD auf BC, ergänzen die Figur durch BAE kongr. ABD und CAF kongr. ACD, und fügen der Figur BCFAE die kongruente CBHA'G hinzu. Wir erhalten so ein Rechteck, denn die Winkel bei E,F,G,H sind rechte und jene bei A,C,A',B gestreckte (gleich 2R), die Grenzlinien also Gerade, und die gegenüberliegenden gleich. Ein Rechteck kann durch eine im Mittelpunkt einer Seite errichtete Senkrechte in zwei kongruente Rechtecke zerlegt werden, und durch Fortsetzung dieses Verfahrens läßt sich die Teilungslinie an eine beliebige Stelle der geteilten Seite bringen.
Dasselbe gilt für das andere Gegenseitenpaar.
Man kann also aus einem gegebenen Rechteck ABCD (Fig. 30) ein kleineres AMQP von beliebigem Seitenverhältnis herausschneiden. Der Diagonalschnitt des letzteren zerlegt dasselbe in zwei kongruente rechtwinklige Dreiecke, deren also jedes (unabhängig vom Seitenverhältnis) die Winkelsumme 2R hat. Jedes schiefwinklige Dreieck kann durch Ziehen einer Höhe in rechtwinklige Dreiecke zerfällt werden, deren jedes wieder ebenso in rechtwinklige Dreiecke von kleinerer Seitenlänge zerlegt werden kann, so daß also 2R als Winkelsumme für jedes Dreieck sich ergibt, wenn dies nur von einem (exakt) gilt. Mit Hilfe dieser auf die[408] Beobachtung aufgebauter Sätze folgert man leicht, daß das Gegenseitenpaar eines Rechteckes (oder überhaupt eines sogenannten Parallelogramms) überall, auch beliebig verlängert, denselben Abstand hat, sich also nicht schneidet. Es hat die Eigenschaften der Euklidischen Parallelen, kann also als solche benannt und definiert werden. Ebenso folgt nun aus den Eigenschaften der Dreiecke und Rechtecke, daß zwei Gerade, welche von einer dritten so geschnitten werden, daß die Summe der Innenwinkel zur selben Seite der letzteren kleiner ist als 2R, nach dieser Seite sich schneiden, zu beiden Seiten des Schnittpunktes sich aber ohne Ende voneinander entfernen. Die Gerade ist demnach unendlich. Was also als Axiom, als Ausgangssatz eine grundlose Behauptung ist, kann als Folgerung einen guten Sinn haben.
20. Die Geometrie besteht also in einer Anwendung der Mathematik auf Raumerfahrungen. Sie wird wie die mathematische Physik nur dadurch zu einer deduktiven exakten Wissenschaft, daß sie die Erfahrungsobjekte durch schematisierende, idealisierende Begriffe darstellt. So wie die Mechanik nur innerhalb der Beobachtungs-Fehlergrenzen die Konstanz der Massen behaupten, die Wechselwirkung der Körper auf bloße Beschleunigungen zurückführen kann, so kann die Existenz von Geraden, Ebenen, der Wert der Winkelsumme u.s.w. nur unter demselben Vorbehalt festgestellt werden. Aber so wie die Physik sich zuweilen veranlaßt sieht, an die Stelle ihrer idealen Annahmen andere, meist allgemeinere zu setzen, statt der konstanten Fallbeschleunigung eine von der Entfernung abhängige, statt der konstanten Wärmemenge eine variable zu setzen u.s.w., so darf dies auch die Geometrie durch die Tatsachen veranlaßt, oder auch nur versuchsweise zur wissenschaftlichen Aufklärung tun.548 So werden uns also jetzt die Versuche von Legendre, Lobatschefskij, der beiden Bolyai, von welchen der jüngere vielleicht indirekt durch Gauß angeregt war, in dem richtigen Lichte erscheinen.
21. Von den Versuchen von Schweickart und Taurinus[409] – ebenfalls Zeitgenossen von Gauß – wollen wir absehen. Lobatschefskijs Arbeiten sind zuerst in weiteren Kreisen bekannt und dadurch wirksam geworden (1829). Sehr bald folgte die Publikation des jüngern Bolyai 1833, der in allen wesentlichen Punkten mit Lobatschefskij übereinstimmt, und nur in der Form seiner Entwicklungen abweicht. Nach den Akten, die jetzt durch die schönen Ausgaben von Engel und Stäckel549 leicht zugänglich geworden sind, und recht vollständig vorliegen, läßt sich annehmen, daß auch Lobatschefskij seine Entwicklungen in der Hoffnung unternommen hat, durch Fallenlassen des Euklidischen Axioms auf Widersprüche geführt zu werden. Nachdem er aber in dieser Erwartung sich getäuscht sah, hatte er den intellektuellen Mut, hieraus alle Konsequenzen zu ziehen. Lobatschefskij gibt seine Entwicklungen in synthetischer Form. Wir können aber die allgemeinen analysierenden Überlegungen uns vergegenwärtigen, welche den Aufbau seiner Geometrie mutmaßlich vorbereitet haben.
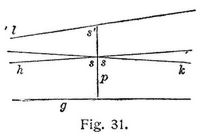
Man nimmt (Fig. 31) außerhalb einer Geraden g einen Punkt an, von welchem man ein Lot p auf g fällt, und durch welchen man in der Ebene gp eine Gerade h zieht, die mit dem Lote einen spitzen Winkel s bildet. Versucht man nun die Annahme, daß g und h sich nicht schneiden, daß aber bei der geringsten Verkleinerung von s dies eintritt, so nötigt die Gleichmäßigkeit des Raumes sofort zu der Folgerung, daß noch eine zweite Gerade k mit demselben Winkel s nach der andern Seite des Lotes sich ebenso verhält. Alle durch denselben Punkt gezogenen nicht schneidenden Geraden liegen dann zwischen h und k. Letztere bilden die Grenze zwischen Schneidenden und Nichtschneidenden, und werden von Lobatschefskij Parallele genannt. Lobatschefskij zeigt sich in der Einleitung zu seinen »Neuen Anfangsgründen der Geometrie« 1835 ganz als Naturforscher. Niemand darf auch nur einem gewöhnlichen besonnenen Menschen die Annahme[410] eines bedeutend unter einem R liegenden »Parallelenwinkels« s zumuten, bei Geraden, die sich so nahe liegen, daß deren Durchschnitt bei geringer Verlängerung augenscheinlich wäre.
Obgleich die hier zu besprechenden Verhältnisse sich nur in roh karikierenden Zeichnungen darstellen lassen, hat man sich doch vielmehr vorzustellen, daß bei den Dimensionen der Zeichnung die Abweichung des s von einem R so klein sei, daß für das Auge h und k ununterscheidbar zusammenfallen. Zieht man nun, das Lot p über den Schnitt mit h verlängernd, durch dessen Endpunkt eine neue Parallele l zu h, die natürlich auch zu g parallel ist, so muß der Parallelenwinkel s'<s sein, wenn wir in Bezug auf h und l nicht wieder auf den Euklidischen Fall zurückkommen sollen. Fährt man so mit der Verlängerung des Lotes und mit dem Parallelenziehen fort, so nimmt der Parallelenwinkel fort und fort ab. Verfolgt man nun weiter abstehende, und daher stärker konvergente Parallele nach der Seite der Konvergenz, so müssen wir konsequenterweise annehmen, daß mit der Annäherung, mit der Verkürzung des Lotes, der Parallelenwinkel wieder zunimmt, um mit dem Vorigen nicht in Widerspruch zu geraten. Der Parallelenwinkel s ist also eine inverse Funktion des Lotes p, welche Lobatschefskij mit II(p) bezeichnet. Eine Schar Parallelen in einer Ebene zeigt die Anordnung der schematischen Fig. 32. Sämtliche Parallelen nähern sich asymptotisch nach der Seite ihrer Konvergenz. Die Gleichmäßigkeit des Raumes fordert, daß jeder »Streifen« zwischen zwei Parallelen mit jedem andern, sobald man nur nach der Längsrichtung die gehörige Verschiebung vornimmt, zur Deckung gebracht werden kann.[411]
22. Lassen wir einen Kreis ins Unbegrenzte wachsen, so müssen dessen Radien aufhören sich zu durchschneiden, sobald beim Anwachsen der zwischenliegenden Bogen ihre Konvergenz dem Parallelismus entspricht. Der Kreis geht dann in die sogenannte »Grenzlinie« über. Analog wird bei unbegrenztem Wachstum die Kugelfläche in eine Fläche umgewandelt, welche Lobatschefskij »Grenzfläche« nennt. Die Grenzlinie steht zur Grenzfläche in analoger Beziehung wie der größte Kreis zur Kugelfläche. Die Geometrie der Kugelfläche ist unabhängig vom Parallelenaxiom. Da sich nun nachweisen läßt, daß Dreiecke aus Grenzlinien auf der Grenzfläche so wenig einen Winkelsummenexzeß darbieten wie endliche sphärische Dreiecke auf einer Kugel von unendlichem Radius, so gelten für jene Grenzdreiecke die Regeln der Euklidischen Geometrie. Um Punkte der Grenzlinie zu finden, bestimmt man an einer Schar Parallelen (in der Ebene): aα, bβ, cγ, dγ,... (Fig. 33) zu einem Punkt a der Geraden aα an den übrigen Parallelen die Punkte b, c, d... so, daß die Winkel αab = βba, αac = γca, αad = δda... werden. Bei der Gleichförmigkeit der ganzen Konstruktion kann jede der Parallelen als »Achse« der Grenzlinie angesehen werden, um welche rotiert die Grenzfläche durch die Grenzlinie beschrieben wird. Ebenso kann jede der Parallelen als Achse der Grenzfläche gelten. Aus demselben Grunde sind alle Grenzlinien und Grenzflächen kongruent. Der Schnitt jeder Ebene mit der Grenzfläche ist ein Kreis, nur wenn die Ebene die Achse enthält, wird aus dem Kreis eine Grenzlinie. In der Euklidischen Geometrie gibt es keine Grenzlinie und Grenzfläche. Die Analoga derselben sind hier die Gerade und die Ebene. Wenn es keine Grenzlinie gibt, müssen drei beliebige nicht in einer Geraden liegende Punkte notwendig auf einem Kreise liegen. Deshalb konnte J. Bolyai durch letztere Forderung das Euklidische Axiom ersetzen.
23. Es seien (Fig. 33) aα, bβ, cγ ... ein System von Parallelen und ae, a1e1, a2e2... ein System von Grenzlinien, von denen jedes das andere in gleiche Teile teilt. Das Verhältnis zweier Grenzbogen zwischen denselben Parallelen, z.B. ad = u und a2d2 = u' hängt dann nur von deren Entfernung aa2 = x ab. Man kann allgemein setzen u/u' = ex/k, wobei k so gewählt ist, daß[412] e die Basis der natürlichen Logarithmen wird. Auf diesem Wege werden die Exponentiellen und durch diese die Hyperbelfunktionen eingeführt. Für den Parallelenwinkel findet sich s = cot1/2Π(p) = ep/k. Für p = 0 wird s = π/2, für p = ∞, s = 0.
Ein Beispiel mag das Verhältnis der Lobatschefskijschen Geometrie zur Euklidischen und sphärischen Geometrie beleuchten. Für das geradlinige Lobatschefskijsche Dreieck mit den Seiten a, b, c und den gegenüberliegenden Winkeln A, B, C ergibt sich, wenn C ein rechter Winkel ist: sh a/k = sh c/k sin A. Hierbei bedeutet sh den hyperbolischen Sinus shx = (ex-e-x)/2, während sin x = (exi-e-xi)/2i, oder shx = x/1! + x3/3! + x5/5! + x7/7! + ... und sin x = x/1! – x3/3! + x5/5! – x7/7! + ...
Berücksichtigt man die im vorigen enthaltenen Relationen sin (xi) = i · shx oder sh (xi) = i · sin x der Kreis- und Hyperbelfunktion, so sieht man, daß die obige Formel für das Lobatschefskijsche Dreieck in die für das sphärische Dreieck gültige sin a/k = sin c/ksin A übergeht, wenn man in ersterer ki an die Stelle von k setzt, und k als den Kugelradius ansieht, der allerdings in den gewöhnlich gebräuchlichen Formeln den Wert 1 annimmt. Die Rückverwandlung der sphärischen Formel in die Lobatschefskijsche auf demselben Wege liegt auf der Hand. Für ein im Verhältnis zu a und c sehr großes k, können wir uns auf das erste Glied der Reihenentwicklung von sh oder sin beschränken, und erhalten in beiden Fällen a /k = c/k · sin A, oder a = c · sin A, die Formel der ebenen Euklidischen Geometrie, welche wir somit als einen Grenzfall sowohl der Lobatschefskij sehen als auch der sphärischen Geometrie für sehr große Werte von k, oder für k = ∞ ansehen können. Wir können auch sagen, im unendlich Kleinen fallen alle drei Geometrien zusammen.[413]
24. Wie man sieht, läßt sich also ein konsequentes, in sich widerspruchsloses System der Geometrie entwickeln, sobald man nur einmal die Konvergenz paralleler Geraden zugegeben hat. Für diese Annahme spricht allerdings keine Beobachtung der uns zugänglichen geometrischen Tatsachen, und dieselbe widerstreitet so sehr unserm geometrischen Instinkt, daß sich daraus das Verhalten der älteren Forscher, wie Saccheri und Lambert, ganz wohl erklärt. Unsere durch die Anschauung und die geläufigen Euklidischen Begriffe geleitete Vorstellung kann auch nur stückweise und nach und nach den Anforderungen einer Lobatschefskijschen Betrachtung gerecht werden. Wir müssen uns hierbei mehr von den mathematischen Begriffen als von den einem kleinen Raumgebiet entstammenden sinnlichen Bildern führen lassen. Man muß jedoch zugeben, daß die mathematischen Quantitätsbegriffe, durch welche wir selbsttätig die Tatsachen der geometrischen Erfahrung darstellen, letzteren nicht absolut entsprechen. Die geometrische Theorie ist wie jene der Physik einfacher und genauer, als dies durch die Erfahrung mit ihren zufälligen Störungen eigentlich verbürgt werden kann. Verschiedene Begriffe können in dem der Beobachtung zugänglichen Gebiete die Tatsachen mit gleicher Genauigkeit ausdrücken. Die Tatsachen sind also wohl zu unterscheiden von den intellektuellen Gebilden, deren Entstehung sie angeregt haben. Die letzteren – die Begriffe – müssen mit der Beobachtung verträglich und außerdem untereinander in logischer Übereinstimmung sein. Diese beiden Forderungen sind eben in mehrfacher Weise erfüllbar, und daher die verschiedenen Systeme der Geometrie.
25. Man sieht es den Arbeiten Lobatschefskijs an, daß sie das Ergebnis langen und angestrengten Nachdenkens sind, und kann vermuten, daß er erst durch allgemeine Erwägungen und analytische (rechnende) Entwicklungen ein klares Bild seines Systems gewonnen haben mußte, bevor er im stande war, dasselbe synthetisch darzustellen. Einladend sind solche Entwicklungen in dieser schwerfälligen Euklidischen Form keineswegs, und es ist vielleicht hauptsächlich dieser Form zuzuschreiben, wenn der Wert der Arbeiten Lobatschefskijs und J. Bolyais so spät allgemein erkannt wurde.[414]
26. Lobatschefskij entwickelte nur die Folgen der Modifikation der fünften Forderung Euklids. Läßt man hingegen den Euklidischen Satz fallen: »zwei Gerade schließen keinen Raum ein«, so gelangt man zu einem Gegenstück der Lobatschefskijschen Geometrie.550 In Beschränkung auf die Fläche ist dies die Geometrie der Kugelfläche. An die Stelle der Euklidischen Geraden treten die größten Kreise, die sich alle zweimal schneiden, und von denen jedes Paar zwei sphärische Zweiecke einschließt. Es gibt also da gar keine Parallelen. Die Möglichkeit einer analogen Geometrie des dreidimensionalen Raumes (von positivem Krümmungsmaß) hat erst Riemann angedeutet. Dieselbe scheint auch von Gauß nicht in Erwägung gezogen worden zu sein, vielleicht aus Vorliebe für die Unendlichkeit des Raumes. Helmholtz551 hingegen, der die Untersuchungen von Riemann in physikalischem Sinne weiterführte, ließ wieder in seiner ersten Publikation den Lobatschefskijschen Fall eines Raumes von negativem Krümmungsmaß (mit imaginärem Parameter k) unbeachtet. In der Tat liegt die Betrachtung dieses Falles dem Mathematiker näher als dem Physiker. Helmholtz behandelt daselbst nur den Euklidischen Fall mit dem Krümmungsmaß Null und den Riemannschen Raum mit positivem Krümmungsmaß.
27. Wir können also die Tatsachen der räumlichen Beobachtung mit aller erreichbaren Genauigkeit darstellen, sowohl durch die Euklidische Geometrie, als auch durch die Lobatschefskijsche und die Riemannsche, wenn wir nur in den beiden letzteren Fällen den Parameter k genügend groß nehmen. Von der Voraussetzung k = ∞ der Euklidischen Geometrie abzugehen, fanden die Physiker bisher keinen Grund. Sie halten nach bewährter zweckmäßiger Übung die einfachsten Voraussetzungen so lange fest, bis die Tatsachen zu einer Komplikation oder Modifikation derselben nötigen. Dies entspricht auch dem Standpunkt aller bedeutenden Mathematiker in Bezug auf angewandte Geometrie. Soweit aber das Verhalten der Naturforscher und der Mathematiker den berührten Fragen gegenüber verschieden[415] ist, erklärt es sich dadurch, daß für erstere das physisch Gegebene die größte Wichtigkeit hat, und die Geometrie nur ein geläufiges Mittel zur Untersuchung desselben ist, während für letztere gerade diese Fragen von größtem fachlichen und insbesondere von erkenntnistheoretischem Interesse sind. Hat aber der Mathematiker einmal versucht die nächsten und einfachsten Voraussetzungen, welche die geometrische Erfahrung an die Hand gibt, zu modifizieren, und hat dieser Versuch sich durch Gewinn an Einsicht gelohnt, so liegt nichts näher, als daß solche Versuche in rein mathematischem Interesse noch weitergeführt werden. Analoga der uns geläufigen Geometrie unter noch freieren, allgemeineren Voraussetzungen, für eine beliebige Dimensionszahl, werden entwickelt, ohne Anspruch, für etwas anderes als wissenschaftliche Gedankenexperimente gehalten zu werden, ohne Absicht der Anwendung auf die sinnliche Wirklichkeit. Es genügt hier auf die Förderung der Mathematik durch Clifford, Klein, Lie u. a. hinzuweisen. Nur selten wird ein Denker so verträumt und der Wirklichkeit abgewandt sein, um an eine die Drei übersteigende Dimensionszahl des uns gegebenen sinnlichen Raumes, oder an die Darstellung desselben durch eine von der Euklidischen merklich abweichenden Geometrie zu denken. Gauß, Lobatschefskij, J. Bolyai, Riemann waren darin ganz klar, und können jedenfalls für die später auf diesem Gebiete auftretenden Monstrositäten nicht verantwortlich gemacht werden.
28. Dem Geschmack des Physikers entspricht es wenig, Voraussetzungen über das Verhalten geometrischer Gebilde im Unendlichen, im Unzugänglichen zu machen, und dieselben nachträglich mit den nächstliegenden Erfahrungen zu vergleichen, und diesen dann erst anzupassen. Er liebt es (ähnlich der Stolzschen Entwicklung) das unmittelbar Gegebene als Quelle seiner Begriffe zu betrachten, die er so lange auch für das Unzugängliche als gültig ansieht, bis er genötigt wird, dieselben zu ändern. Aber auch er darf für die Aufklärung, daß es mehrere genügende Geometrien gibt, daß man auch mit einem endlichen Raum das Auskommen finden kann u.s.w., kurz für die Beseitigung konventioneller Schranken des Denkens recht dankbar sein. Würden wir, auf der Oberfläche eines Planeten mit trüber, undurchsichtiger[416] Atmosphäre lebend, nur auf Winkelmaß und Meßkette angewiesen, von der Voraussetzung einer ebenen Oberfläche ausgehend Vermessungen beginnen, so würde uns das Anwachsen eines Winkelsummenexzesses bei größeren Dreiecken alsbald nötigen, unsere Planimetrie mit einer Sphärometrie zu vertauschen. Die Möglichkeit analoger Erfahrungen im dreidimensionalen Raum kann der Physiker im Prinzip nicht ausschließen, wenngleich die Erscheinungen, die zur Annahme einer Lobatschefskijschen oder Riemannschen Geometrie nötigen würden, so abenteuerlich mit dem bisher Gewohnten im Gegensatz stehen würden, daß niemand den Eintritt derselben für wahrscheinlich halten wird.
29. Die Frage, ob ein vorgelegtes physikalisches Objekt eine Gerade oder ein Kreisbogen sei, ist nicht in richtiger Form gestellt. Eine gespannte Schnur oder ein Lichtstrahl ist gewiß weder das eine noch das andere. Es kann sich nur darum handeln, ob das Objekt räumlich so reagiert, daß es besser dem einen als dem anderen Begriff entspricht, und ob es mit der uns genügenden und erreichbaren Genauigkeit überhaupt einem der geometrischen Begriffe entspricht. Wenn der letztere Fall nicht gegeben ist, so fragt es sich, ob wir die Abweichung von der Geraden oder vom Kreise praktisch beseitigen oder wenigstens in Gedanken bestimmen und berücksichtigen, also das Ergebnis der Messung korrigieren können. Bei der praktischen Messung sind wir jedoch immer auf die Vergleichung physikalischer Objekte angewiesen. Würden diese bei direkter Untersuchung mit aller erreichbaren Genauigkeit den geometrischen Begriffen entsprechen, die indirekten Ergebnisse der Messung aber von der Theorie mehr abweichen, als nach den möglichen Fehlern zulässig erscheint, so müßten wir unsere physikalisch-metrischen Begriffe allerdings ändern. Der Physiker wird gut tun, den Eintritt dieser Situation abzuwarten, während der Mathematiker für seine Überlegungen stets freien Spielraum hat.
30. Die Raum- und Zeitbegriffe des Naturforschers sind die einfachsten. Räumliche und zeitliche Objekte, welche seinen Begriffskonstruktionen entsprechen, können mit großer Genauigkeit hergestellt werden. Fast jede Abweichung, die noch bemerkt werden kann, läßt sich auch beseitigen. Jede Raum- oder Zeitkonstruktion kann man sich verwirklicht denken, ohne einer Tatsache[417] Gewalt anzutun. Die übrigen physikalischen Eigenschaften der Körper hängen so voneinander ab, daß hier die willkürlichen Fiktionen eine enge Schranke an den Tatsachen finden. Ein vollkommenes Gas, eine vollkommene Flüssigkeit, ein vollkommen elastischer Körper existiert nicht; der Physiker weiß, daß seine Fiktionen den Tatsachen nur annähernd, willkürlich vereinfachend entsprechen; er kennt die Abweichung, die nicht beseitigt werden kann. Eine Kugel, Ebene u.s.w. kann man in beliebiger Genauigkeit hergestellt denken, ohne mit einer Tatsache in Widerspruch zu geraten. Sollte also irgend eine physikalische Tatsache Modifikation unserer Begriffe fordern, so wird der Physiker lieber die weniger vollkommenen Begriffe der Physik opfern, als die einfacheren, vollkommeneren, festeren der Geometrie, welche die solideste Grundlage aller seiner Konzeptionen bilden.
31. Nach einer anderen Richtung kann aber der Physiker aus den Arbeiten der Geometer wesentlichen Nutzen schöpfen. Unsere Geometrie bezieht sich immer auf Objekte der sinnlichen Erfahrung. Sobald wir aber mit bloßen Gedankendingen, wie Atome und Moleküle, operieren, die ihrer Natur nach nicht in die Sinne fallen können, haben wir kein Recht mehr, dieselben notwendig in Beziehungen, in relativen Lagen zu denken, die dem Euklidischen dreidimensionalen Raum unserer sinnlichen Erfahrung angehören. Dies haben insbesondere diejenigen zu bedenken, welche atomistische Betrachtungen für unentbehrlich halten.552
32. Denken wir an den Ursprung der Geometrie aus dem[418] praktischen Bedürfnis zurück. Die räumliche Substanzialität, die räumliche Unveränderlichkeit eines Raumdinges trotz dessen Bewegung zu erkennen, ist für uns biologische Notwendigkeit, weil das Raumquantum zur Quantität der Bedürfnisbefriedigung in Beziehung steht. Soweit diese Kenntnis nicht schon durch unsere physiologische Organisation genügend verbürgt ist, benützen wir unsere Hände und Füße zur Vergleichung mit dem räumlichen Objekt. Mit der Vergleichung der Körper untereinander treten wir aber schon in das Gebiet der Physik ein, ob wir die Hände oder einen künstlichen Maßstab verwenden. Alle physikalischen Bestimmungen sind relativ. So gelten auch alle geometrischen Bestimmungen relativ zum Maßstab. Der Maßbegriff ist ein Relationsbegriff, welcher über den Maßstab selbst nichts mehr aussagt. Wir nehmen in der Geometrie nur an, daß der Maßstab immer und überall deckt, was derselbe irgendwo und irgendwann einmal gedeckt hat. Über den Maßstab selbst bestimmt dies nichts. Es tritt hiermit an die Stelle der räumlichen physiologischen Gleichheit eine ganz anders definierte physikalische, die mit jener nicht verwechselt werden darf, so wie man eine Thermometeranzeige nicht mit der Wärmeempfindung identifizieren darf. Zwar konstatiert der praktische Geometer die Ausdehnung eines erwärmten Maßstabes durch einen auf konstanter Temperatur gehaltenen Maßstab und nimmt darauf Rücksicht, daß durch diesen raumfremden physikalischen Umstand jene Kongruenzbeziehung gestört wird, allein der reinen Raumlehre liegt eine Voraussetzung über den Maßstab fern. Es wird nur die aus physiologischer Quelle stammende Gewohnheit, den Maßstab als unveränderlich anzusehen, stillschweigend aber unberechtigt festgehalten. Es würde ganz müßig sein und keinerlei Sinn haben, wollte man annehmen, daß der Maßstab, also die Körper überhaupt mit der Verschiebung im Raume Veränderungen erfahren oder unverändert bleiben, was wieder nur durch einen neuen Maßstab konstatiert werden könnte. Die Relativität aller räumlichen Beziehungen offenbart sich durch diese Überlegung.
33. Wird das Kriterium der räumlichen Gleichheit schon durch Einführung des Maßes wesentlich modifiziert, so erfährt es eine weitere Modifikation, bezw. Verschärfung, durch Einführung des Zahlbegriffes in die Geometrie. Es wird hierdurch eine Feinheit[419] der Unterscheidung bedingt, welche der bloße Kongruenzbegriff niemals vermitteln könnte. Nur die Anwendung der Arithmetik auf die Geometrie führt zu den Begriffen des Inkommensurablen, des Irrationalen. Unsere geometrischen Begriffe enthalten also raumfremde Zutaten; sie stellen das Räumliche mit einer gewissen Freiheit und namentlich willkürlich mit einer größeren Genauigkeit dar, als dies die räumliche Beobachtung zu erreichen vermag. Der unvollständige Kontakt zwischen Tatsache und Begriff macht eben die Möglichkeit verschiedener geometrischer Systeme (Theorien) verständlich.553 Genau dasselbe läßt sich aber auch in Bezug auf die Physik sagen.554
34. Die ganze Entwicklung, welche zur Umwandlung in der Auffassung der Geometrie geführt hat, muß als eine gesunde und kräftige Bewegung bezeichnet werden. Diese Bewegung, seit Jahrhunderten vorbereitet, in unseren Tagen erheblich gesteigert, ist keineswegs schon als abgeschlossen zu betrachten. Wir dürfen vielmehr erwarten, daß dieselbe nicht nur der Mathematik und Geometrie, namentlich in erkenntnistheoretischer Beziehung, sondern auch den andern Wissenschaften noch die reichsten Früchte bringen wird. Diese Bewegung verdankt zwar einzelnen bedeutenden Menschen mächtige Anregungen, dieselbe ist aber trotzdem nicht einem individuellen, sondern einem allgemeinen Bedürfnis entsprungen. Man sieht dies schon aus dem verschiedenen Beruf der Menschen, die sich an dieser Bewegung beteiligten. Nicht nur Mathematiker, auch Philosophen und Didaktiker lieferten Beiträge zu den betreffenden Untersuchungen. Auch die von verschiedenen Forschern eingeschlagenen Wege führen nahe aneinander vorbei. Gedanken, welche Leibniz555 äußert, kehren in wenig veränderter Form wieder bei Fourier,556 Lobatschefskij, J. Bolyai, H. Erb.557 Indem der Philosoph [420] Überweg558 in seiner Opposition gegen Kant wesentlich an den Psychologen Beneke,559 mit seinen geometrischen Ausführungen an H. Erb anknüpft, welcher letztere wieder in K. A. Erb560 einen Vorgänger nennt, nimmt Überweg einen guten Teil der Helmholtzschen Arbeit vorweg.
35. Die Ergebnisse, zu welchen die hier besprochene Entwicklung geführt hat, lassen sich wie folgt zusammenfassen:
1. Die Erfahrung wurde als Quelle unserer geometrischen Begriffe erkannt.
2. Die Vielfachheit der denselben geometrischen Tatsachen genügenden Begriffe wurde klargelegt.
3. Durch die Vergleichung des Raumes mit anderen Mannigfaltigkeiten wurden allgemeinere Begriffe gewonnen, von welchen die geometrischen einen besonderen Fall darstellen. Dadurch wurde das geometrische Denken von konventionellen, für unüberschreitbar gehaltenen Schranken befreit.
4. Durch den Nachweis dem Raume verwandter, von demselben verschiedener Mannigfaltigkeiten wurden ganz neue Fragen nahegelegt. Was ist der Raum physiologisch, physikalisch, geometrisch? Worauf sind dessen besondere Eigenschaften zurückzuführen, da doch andere auch denkbar sind? Warum ist derselbe dreidimensional? u. s. w.
36. Mit solchen Fragen, wenn wir deren Beantwortung auch nicht heute und nicht morgen erwarten, stehen wir vor der ganzen Tiefe des noch zu Erforschenden. Von den unberufenen Urteilen der »Böoter«, die Gauß kommen sah und die ihn so zurückhaltend stimmten, wollen wir schweigen. Was sollen wir aber zu den herben und nörgelnden Kritiken sagen, die Gauß, [421] Riemann und deren Genossen für die gebotenen Aufklärungen von selten wissenschaftlich hochstehender Männer erfahren mußten? Sollten es diese nie am eigenen Leibe erfahren haben, daß der Forscher an den äußersten Grenzen des Wissens manches findet, das nicht gleich glatt in jeden Kopf drein geht, das darum aber noch kein Unsinn ist? Gewiß sind solche Forscher auch dem Irrtum ausgesetzt. Aber selbst die Irrtümer mancher Menschen sind in ihren Folgen oft fruchtbarer als die Entdeckungen anderer.[422]
| 526 | Dieser Artikel ist in »The Monist«, Vol. XIV. Oktober 1903 erschienen. Ich versuche hier als Physiker zur sogenannten Metageometrie Stellung zu nehmen. Ausführliche geometrische Entwicklungen muß man in den Quellen nachsehen. Ich hoffe jedoch durch Hinweis auf jedem bekannte und geläufige Beispiele allgemein verständlich zu bleiben. – Gegen die folgenden Ausführungen hat Professor F. Brentano mündlich und brieflich Einwendungen erhoben, die mir zu denken geben, die ich jedoch jetzt, mit andern Dingen beschäftigt, nicht genügend erwägen kann. |
| 527 | Über die Hypothesen, welche der Geometrie zu Grunde liegen. Göttingen 1867. |
| 528 | Brief von Gauß an Bessel, 27. Januar 1829. |
| 529 | Brief von Gauß an Bessel vom 9. April 1830. – Der Ausdruck: »Die Zahl ist Produkt oder Schöpfung des Geistes« wird seither von den Mathematikern wiederholt gebraucht. Unbefangene psychologische Beobachtung lehrt jedoch, daß die Bildung des Zahlbegriffes ebenso durch die Erfahrung eingeleitet wird, wie die Bildung der geometrischen Begriffe. Mindestens muß man die Erfahrung gemacht haben, daß in gewissem Sinne gleichwertige Objekte mehrfach und unveränderlich vorhanden sind, bevor Zahlbegriffe sich bilden können. Auch das Zählexperiment spielt in der Entwicklung der Arithmetik eine bedeutende Rolle. |
| 530 | Wenn Tonhöhe, Stärke und Klangfarbe, wenn Farbenton, Sättigung und Lichtstärke mit den 3 Dimensionen des Raumes in Analogie gesetzt werden, so wird dies wenige Menschen befriedigen. Die Klangfarbe, sowie der Farbenton ist von mehreren Variablen abhängig. Wenn also die Analogie überhaupt einen Sinn hat, entsprechen der Klangfarbe und dem Farbenton mehrere Dimensionen. – Vgl. Benno Erdmann, Die Axiome der Geometrie. Leipzig 1877. |
| 531 | Auf diese Analogie bin ich 1863 beim Studium des Gehörorgans aufmerksam geworden, und habe sie seither weiter verfolgt. S. »Analyse der Empfindungen«. 4. Aufl. S. 222 u. f. |
| 532 | Vgl. S. 345. |
| 533 | Ich gestehe, daß ich als junger Student über jede Ableitung mit Symbolen, deren Bedeutung nicht ganz klar und anschaulich war, mich empörte. Das historische Studium ist aber wohl geeignet den Hang zur Mystik zu beseitigen, der durch die traumhafte Anwendung solcher Methoden leicht begünstigt und anerzogen wird, indem dasselbe den heuristischen Wert dieser Methoden kennen lehrt, und zugleich erkenntnistheoretisch aufklärt, worin die Hilfe, die sie leisten, besteht. Eine symbolische Darstellung einer Rechnungsoperation hat für den Mathematiker dieselbe Bedeutung, wie ein Modell oder eine anschauliche Arbeitshypothese für den Physiker. Das Symbol, das Modell, die Hypothese geht dem Darzustellenden parallel. Aber der Parallelismus kann weiter reichen, oder weiter geführt werden, als es bei Wahl dieser Mittel ursprünglich beabsichtigt war. Indem das Dargestellte und das Darstellungsmittel doch verschieden ist, fällt an dem einen auf, was an dem andern verborgen bleiben würde. Auf eine Operation a2/3 könnte man schwerlich unmittelbar verfallen. Die Rechnung mit solchen Symbolen führt aber dazu, diesem Symbol einen verständlichen Sinn beizulegen. Man rechnete nach dem Vorgange von Euler viele Decennien mit Ausdrücken wie cos x+√-1 · sin x, und mit Exponentiellen mit imaginären Exponenten, bis in dem Streben der gegenseitigen Anpassung von Gedanke und Symbol endlich durch Argand 1806 die seit einem Jahrhundert keimende Idee durchbrach, daß ein Verhältnis nach Größe und Richtung aufgefaßt werden könne, wodurch sich √-1 als mittlere Richtungsproportionale zwischen +1 und -1 herausstellte. |
| 534 | Wären die 6 Grundfarbenempfindungen voneinander ganz unabhängig, so würde das System der Farbenempfindungen eine fünffache Mannigfaltigkeit darstellen. Da sie paarweise im Gegensatz stehen, entspricht das System einer dreifachen Mannigfaltigkeit. |
| 535 | Vgl. S. 374, 375. |
| 536 | Disquisitiones generales circa superficies curvas. 1827. |
| 537 | Über die Tatsachen, welche der Geometrie zu Grunde liegen. Göttinger Nachrichten. 1868. 3. Juni. |
| 538 | Vgl. z.B. Kronecker, Über Systeme von Funktionen mehrerer Variablen. Ber. d. Berliner Akademie. 1869. |
| 539 | Vgl. S. 351, 376. |
| 540 | C. R. Kosack, Beiträge zu einer systematischen Entwicklung der Geometrie aus der Anschauung. Nordhausen 1852. – Dieses Programm hat mir Herr Prof. F. Pietzker in Nordhausen gütigst zur Ansicht gesendet. – Ähnliche einfache Ableitungen finden sich bei Bernhard Becker, Leitfaden für den ersten geometrischen Unterricht in der Geometrie. Frankfurt a. M. 1874, und in desselben Verfassers Schrift: Über die Methode des geometrischen Unterrichts. Frankfurt a. M. 1845. – Erstere Schrift erhielt ich durch die Güte des Herrn Dr. M. Schuster in Oldenburg i. Gr. zur Einsicht. |
| 541 | Das Euklidische System hat durch seine logischen Vorzüge bestochen. Darüber wurden dessen übrige Mängel übersehen. Große Forscher bis in die moderne Zeit hinein haben sich verleiten lassen, bei Darstellung ihrer Forschungsergebnisse dem Beispiel Euklids zu folgen und zum Nachteile der Wissenschaft ihre Forschungswege zu verdecken. Allein die Wissenschaft ist kein Advokatenkunststück. Die wissenschaftlichste Darstellung ist jene, welche alle Motive eines Gedankens so darlegt, daß sie jederzeit auf ihre Kraft und Stichhaltigkeit nachgeprüft werden können. Nicht mit halbverbundenen Augen soll der Lernende geführt werden. Es erhob sich deshalb unter den Philosophen und Didaktikern Deutschlands auch eine gesunde Reaktion, welche namentlich von Herbart, Schopenhauer und Trendelenburg ausging. Man bemühte sich größere Anschaulichkeit, eine mehr genetische Methode und logisch durchsichtigere Ableitungen in den Unterricht einzuführen. – Vgl. die modernen Schriften: M. Pasch (Vorlesungen über neuere Geometrie. Leipzig 1882). – D. Hilbert (Grundlagen der Geometrie. Leipzig 1899). |
| 542 | Euklides ab omni naevo vindicatus. Mediolani 1733. Übersetzt in Engel und Stäckel, Die Theorie der Parallellinien. Leipzig 1895. |
| 543 | Engel und Stäckel, l. c., S. 21 u. f. |
| 544 | Ebenda S. 152 u. f. |
| 545 | Vgl. Anmerkung S. 396. |
| 546 | Gauß zum Gedächtnis. Leipzig 1856. |
| 547 | Das letzte Axiom der Geometrie. Berichte des naturw.-medizin. Vereins zu Innsbruck. 1886. S. 25-34. |
| 548 | Den Unterschied zwischen Geometrie und Physik, den Duhem (La Theorie physique, p. 290) als einen fundamentalen qualitativen auffaßt, halte ich nur für einen Gradunterschied. |
| 549 | F. Engel, N. I. Lobatschefskij, Zwei geometrische Abhandlungen. Leipzig 1899. |
| 550 | Vgl. die S. 379 zitierte Abhandlung von De Tilly. |
| 551 | Über die tatsächlichen Grundlagen der Geometrie. 1866. Wissenschaftliche Abhandlungen. II, S. 610 u. f. |
| 552 | Noch in der atomistischen Theorie befangen, versuchte ich die Linienspektren der Gase durch die Schwingungen der Atombestandteile eines Gasmoleküls gegeneinander zu erklären. Die Schwierigkeiten, die ich hierbei fand, legten mir 1863 den Gedanken nahe, daß nichtsinnliche Dinge nicht notwendig in unserem sinnlichen Raume von drei Dimensionen vorgestellt werden müssen. So kam ich auf Analoga des Raumes von verschiedener Dimensionszahl. Gleichzeitiges Studium verschiedener physiologischer Mannigfaltigkeiten (S. 393) führte mich zu den am Schlusse dieses Kapitels berührten Fragen. Der Gedanke endlicher Räume, konvergierender Parallelen u.s.w., der sich nur durch das historische Studium der Geometrie ergeben konnte, lag mir damals fern. Ich glaube, daß meine Kritiker gut getan hätten, die gesperrt gedruckte Klausel nicht zu übersehen. Näheres in den Anmerkungen zu »Erhaltung der Arbeit«. Prag 1872. Vgl. auch die Ausführungen in Vaihinger, Die Philosophie des als ob. Berlin 1911. |
| 553 | Wir dürfen der Materie nicht zumuten, alle die atomistischen Phantasien des Physikers zu verwirklichen. Ebensowenig wird der Raum (als Erfahrungsobjekt) allen Ideen des Mathematikers genügen, womit kein Zweifel an dem Wert der betreffenden Untersuchungen an sich ausgesprochen sein soll. |
| 554 | Vgl. die Anmerkung S. 409. |
| 555 | Vgl. S. 369, 370. |
| 556 | Séances des Écoles normales. Débats. T. I. 1800. p. 28. |
| 557 | H. Erb, Großherzoglich Badischer Finanzrat, Die Probleme der geraden Linie, des Winkels und der ebenen Fläche. Heidelberg 1846. Erb hat hier jene Ergänzung der Elementargeometrie gegeben, die Gauß in einem Briefe an Bessel verlangt. In derselben Richtung arbeitet J. Schram in seiner als Manuskript gedruckten, 1903 von Obersteig in Nordtirol datierten Abhandlung: »Leibnizens Definitionen der Ebene und der Geraden«. |
| 558 | Die Prinzipien der Geometrie wissenschaftlich dargestellt. Archiv für Philologie und Pädagogik. 1851. Abgedruckt in Brasch, Welt- und Lebensanschauung F. Überwegs. Leipzig 1889. S. 263-317. |
| 559 | Logik als Kunstlehre des Denkens. Berlin 1842. II. Bd., S. 51-55. |
| 560 | Zur Mathematik und Logik. Heidelberg 1821. Diese Schrift blieb mir unzugänglich. – Leser von vorwiegend philosophischem Interesse seien noch auf die S. 387 zitierte Arbeit von C. Siegel verwiesen. |
|
Ausgewählte Ausgaben von
Erkenntnis und Irrtum
|
Buchempfehlung
Hoffmann, E. T. A.
Meister Floh. Ein Märchen in sieben Abenteuern zweier Freunde
Als einen humoristischen Autoren beschreibt sich E.T.A. Hoffmann in Verteidigung seines von den Zensurbehörden beschlagnahmten Manuskriptes, der »die Gebilde des wirklichen Lebens nur in der Abstraction des Humors wie in einem Spiegel auffassend reflectirt«. Es nützt nichts, die Episode um den Geheimen Hofrat Knarrpanti, in dem sich der preußische Polizeidirektor von Kamptz erkannt haben will, fällt der Zensur zum Opfer und erscheint erst 90 Jahre später. Das gegen ihn eingeleitete Disziplinarverfahren, der Jurist Hoffmann ist zu dieser Zeit Mitglied des Oberappellationssenates am Berliner Kammergericht, erlebt er nicht mehr. Er stirbt kurz nach Erscheinen der zensierten Fassung seines »Märchens in sieben Abenteuern«.
128 Seiten, 5.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Große Erzählungen der Hochromantik
Zwischen 1804 und 1815 ist Heidelberg das intellektuelle Zentrum einer Bewegung, die sich von dort aus in der Welt verbreitet. Individuelles Erleben von Idylle und Harmonie, die Innerlichkeit der Seele sind die zentralen Themen der Hochromantik als Gegenbewegung zur von der Antike inspirierten Klassik und der vernunftgetriebenen Aufklärung. Acht der ganz großen Erzählungen der Hochromantik hat Michael Holzinger für diese Leseausgabe zusammengestellt.
- Adelbert von Chamisso Adelberts Fabel
- Jean Paul Des Feldpredigers Schmelzle Reise nach Flätz
- Clemens Brentano Aus der Chronika eines fahrenden Schülers
- Friedrich de la Motte Fouqué Undine
- Ludwig Achim von Arnim Isabella von Ägypten
- Adelbert von Chamisso Peter Schlemihls wundersame Geschichte
- E. T. A. Hoffmann Der Sandmann
- E. T. A. Hoffmann Der goldne Topf
390 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum