Online-Bibliothek

5

[84] Als man im Kreise der Pythagoräer um 540 zu der Einsicht kam, daß das Wesen aller Dinge die Zahl sei, da wurde nicht »in der Entwicklung der Mathematik ein Schritt vorwärts getan«, sondern es wurde eine ganz neue Mathematik aus der Tiefe des antiken Seelentums geboren, als selbstbewußte Theorie, nachdem sie in metaphysischen[84] Fragestellungen und künstlerischen Formtendenzen sich längst angekündigt hatte. Eine neue Mathematik, wie die stets ungeschrieben gebliebene der ägyptischen und wie die algebraisch-astronomisch gestaltete der babylonischen Kultur mit ihren ekliptischen Koordinatensystemen, die beide in einer großen Stunde der Geschichte einmal geboren wurden und damals längst erloschen waren. Die im 2. Jahrhundert v. Chr. vollendete antike Mathematik verschwand aus der Welt trotz ihres in unsrer Bezeichnungsweise noch heute währenden Scheindaseins, um der arabischen in der Ferne Platz zu machen. Was wir von der alexandrinischen Mathematik wissen, setzt eine große Bewegung auf diesem Gebiete voraus, deren Schwerpunkt durchaus in den persisch-babylonischen Hochschulen wie Edessa, Dschondisabur und Ktesiphon gelegen haben muß, und die nur mit Einzelheiten in das antike Sprachgebiet hinübergriff. Die Mathematiker in Alexandria sind trotz ihrer griechischen Namen – Zenodoros, der die isoperimetrischen Figuren behandelte, Serenos, der mit den Eigenschaften eines harmonischen Strahlenbüschels im Raum arbeitete, Hypsikles, der die chaldäische Kreisteilung eingeführt hat, und vor allem Diophant – zweifellos sämtlich Aramäer und ihre Schriften nur ein kleiner Teil einer vorwiegend syrisch geschriebenen Literatur.7 Diese Mathematik fand in der arabisch-islamischen Forschung ihren Abschluß, und es folgte nach langer Zwischenzeit, wieder als eine ganz neue Schöpfung eines neuen Bodens, die abendländische, unsere Mathematik, die wir in seltsamer Verblendung als die Mathematik, den Gipfel und das Ziel einer zweitausendjährigen Entwicklung, ansehen und deren heute fast abgelaufene Jahrhunderte ebenso streng bemessen sind.

Jener Ausspruch, daß die Zahl das Wesen aller sinnlich greifbaren Dinge darstelle, ist der wertvollste der antiken Mathematik geblieben. Mit ihm ist die Zahl als Maß definiert worden. Darin liegt das ganze Weltgefühl einer dem Jetzt und Hier leidenschaftlich zugewendeten Seele. Messen in diesem Sinne heißt etwas Nahes und Körperhaftes messen. Denken wir an den Inbegriff des antiken Kunstwerkes, die freistehende Bildsäule eines nackten Menschen: hier ist alles[85] Wesentliche und Bedeutsame des Daseins, dessen ganzer Rhythmus, erschöpfend durch Flächen, Maße und die sinnlichen Verhältnisse der Teile gegeben. Der pythagoräische Begriff der Harmonie der Zahlen, obwohl vielleicht aus einer Musik abgeleitet, welche die Polyphonie und Harmonie nicht kannte und durch die Ausbildung ihrer Instrumente einen pastosen, fast körperhaften Einzelton anstrebte, scheint durchaus für das Ideal dieser Plastik geprägt zu sein. Der behandelte Stein ist nur insofern ein Etwas, als er abgewogene Grenzen und gemessene Form besitzt, als das, was er unter dem Meißel des Künstlers geworden ist. Abgesehen davon ist er Chaos, etwas noch nicht Verwirklichtes, vorläufig also ein Nichts. Dies Gefühl, ins Große übertragen, schafft als Gegensatz zum Zustand des Chaos den des Kosmos, die abgeklärte Lage in der Außenwelt der antiken Seele, die harmonische Ordnung aller wohlbegrenzten und greifbar gegenwärtigen Einzeldinge. Die Summe dieser Dinge ist bereits die ganze Welt. Der Abstand zwischen ihnen, unser mit dem ganzen Pathos eines großen Symbols erfüllter Weltraum, ist nichts, τὸ μὴ ὄν. Ausdehnung heißt für den antiken Menschen Körperlichkeit, für uns Raum, als dessen Funktion die Dinge »erscheinen«. Von hier aus rückwärts blickend enträtseln wir vielleicht den tiefsten Begriff der antiken Metaphysik, das ἄπειρον Anaximanders, das sich in keine Sprache des Abendlandes übersetzen läßt: es ist das, was keine »Zahl« im pythagoräischen Sinne besitzt, keine gemessene Größe und Grenze, kein Wesen also; das Maßlose, die Unform, eine Statue, die noch nicht aus dem Blocke herausgemeißelt ist. Dies ist die ἀρχή, das optisch Grenzen- und Formlose, das erst durch Grenzen, durch sinnliche Vereinzelung ein Etwas, die Welt nämlich, wird. Es ist das, was der antiken Erkenntnis als Form a priori zugrunde liegt, Körperlichkeit an sich, und an dessen Stelle im kantischen Weltbilde genau entsprechend der Raum erscheint, aus dem Kant sich angeblich »alle Dinge fortdenken konnte«.

Man wird jetzt begreifen, was eine Mathematik von der andern, was insbesondere die antike von der abendländischen scheidet. Das reife antike Denken konnte seinem ganzen Weltgefühl nach in der Mathematik nur die Lehre von den Größen-, Maß- und Gestaltverhältnissen[86] leibhafter Körper sehen. Wenn Pythagoras aus diesem Gefühl heraus die entscheidende Formel aussprach, so war eben für ihn die Zahl ein optisches Symbol, nicht Form überhaupt oder abstrakte Beziehung, sondern das Grenzzeichen des Gewordenen, insofern dieses in sinnlich übersehbaren Einzelheiten auftritt. Zahlen werden von der gesamten Antike ohne Ausnahme als Maßeinheiten, als Größen, Strecken, Flächen aufgefaßt. Eine andere Art Ausdehnung ist ihr nicht vorstellbar. Alle antike Mathematik ist im letzten Grunde Stereometrie. Euklid, der im 3. Jahrhundert ihr System abschloß, meint, wenn er von einem Dreieck spricht, mit innerster Notwendigkeit die Grenzfläche eines Körpers, niemals ein System dreier sich schneidender Geraden oder eine Gruppe dreier Punkte im Raum von drei Dimensionen. Er bezeichnet die Linie als »Länge ohne Breite« (μῆκος ἀπλατές). In unserm Munde würde diese Definition kläglich sein. Innerhalb der antiken Mathematik ist sie ausgezeichnet.

Auch die abendländische Zahl ist nicht, wie Kant und selbst Helmholtz dachten, aus der Zeit als einer Form a priori der Anschauung hervorgegangen, sondern als Ordnung gleichartiger Einheiten etwas spezifisch Räumliches. Die wirkliche Zahl hat, wie sich immer deutlicher zeigen wird, mit mathematischen Dingen nicht das Geringste zu tun. Zahlen gehören ausschließlich in die Sphäre des Ausgedehnten. Aber es gibt so viele Möglichkeiten und also Notwendigkeiten, Ausgedehntes geordnet vorzustellen, als es Kulturen gibt. Die antike Zahl ist nicht ein Denken räumlicher Beziehungen, sondern für das leibliche Auge abgegrenzter, greifbarer Einheiten. Die Antike kennt deshalb – das folgt mit Notwendigkeit – nur die »natürlichen« (positiven, ganzen) Zahlen, die unter den vielen, äußerst abstrakten Zahlenarten der abendländischen Mathematik, den komplexen, hyperkomplexen, nichtarchimedischen u.a. Systemen eine durch nichts ausgezeichnete Rolle spielen.

Deshalb ist die Vorstellung irrationaler Zahlen, in unserer Schreibweise also unendlicher Dezimalbrüche, dem griechischen Geist unvollziehbar geblieben. Euklid sagt – und man hätte ihn besser verstehen sollen –, daß inkommensurable Strecken sich »nicht wie Zahlen«[87] verhalten. In der Tat liegt im vollzogenen Begriff der irrationalen Zahl die völlige Trennung des Zahlbegriffs vom Begriff der Größe und zwar deshalb, weil eine solche Zahl, Π z.B., niemals abgegrenzt oder exakt durch eine Strecke dargestellt werden kann. Daraus folgt aber, daß in der Vorstellung etwa des Verhältnisses der Quadratseite zur Diagonale die antike Zahl, die durchaus sinnliche Grenze, abgeschlossene Größe ist, plötzlich an eine ganz andere Art der Zahl rührt, die dem antiken Weltgefühl im tiefsten Innern fremd und darum unheimlich bleibt, als sei man nahe daran, ein gefährliches Geheimnis des eignen Daseins aufzudecken. Dies verrät ein seltsamer spätgriechischer Mythos, wonach derjenige, welcher zuerst die Betrachtung des Irrationalen aus dem Verborgnen an die Öffentlichkeit brachte, durch einen Schiffbruch umgekommen sei, »weil das Unaussprechliche und Bildlose immer verborgen bleiben solle«. Wer die Angst fühlt, welche diesem Mythos zugrunde liegt – es ist dieselbe, welche den Griechen der reifsten Zeit vor der Ausdehnung seiner winzigen Stadtstaaten zu politisch organisierten Landschaften, vor der Anlage weiter Straßenfluchten und Alleen mit Fernblicken und berechneten Abschlüssen, vor der babylonischen Astronomie mit ihrer Durchdringung endloser Sternenräume und vor dem Verlassen des Mittelmeeres auf Bahnen, welche die Schiffe der Ägypter und Phöniker längst erschlossen hatten, immer wieder zurückschrecken ließ; es ist die tiefe metaphysische Angst vor der Auflösung des Greifbar-Sinnlichen und Gegenwärtigen, mit dem sich das antike Dasein wie mit einer Schutzmauer umgeben hatte, hinter der etwas Unheimliches, ein Abgrund und Urgrund dieses gewissermaßen künstlich geschaffenen und behaupteten Kosmos schlief –, wer dies Gefühl begreift, der hat auch den letzten Sinn der antiken Zahl, des Maßes im Gegensatz zum Unermeßlichen, und das hohe religiöse Ethos in ihrer Beschränkung begriffen. Goethe als Naturforscher hat es sehr wohl gekannt – daher seine fast ängstliche Auflehnung gegen die Mathematik, die sich in Wirklichkeit, was noch niemand recht verstanden hat, unwillkürlich durchaus gegen die nichtantike Mathematik, die der Naturlehre seiner Zeit zugrunde liegende Infinitesimalrechnung richtete.[88]

Die antike Religiosität sammelt sich mit steigendem Nachdruck in sinnlich gegenwärtigen – ortsgebundenen – Kulten, die allein einem »euklidischen« Göttertum entsprechen. Abstrakte, in den heimatlosen Räumen des Denkens schwebende Dogmen sind ihm immer fern geblieben. Ein solcher Kult und ein päpstliches Dogma verhalten sich wie die Statue zur Orgel im Dom. Es haftet der euklidischen Mathematik zweifellos etwas Kultisches an. Man denke an die Geheimlehre der Pythagoräer und an die Lehre von den regelmäßigen Polyedern mit ihrer Bedeutung für die Esoterik des platonischen Kreises. Dem entspricht andrerseits eine tiefe Verwandtschaft der Analysis des Unendlichen von Descartes an mit der gleichzeitigen Dogmatik in ihrem Fortschreiten von den letzten Entscheidungen der Reformation und Gegenreformation bis zu einem reinen, von allen sinnlichen Bezügen gelösten Deismus. Descartes und Pascal waren Mathematiker und Jansenisten. Leibniz war Mathematiker und Pietist. Voltaire, Lagrange und d'Alembert sind Zeitgenossen. Man empfand aus dem antiken Seelentum heraus das Prinzip des Irrationalen, also die Zerstörung der statuarischen Reihe der ganzen Zahlen, der Repräsentanten einer in sich vollkommenen Weltordnung, als einen Frevel gegen das Göttliche selbst. Bei Plato, im »Timäus«, ist dies Gefühl unverkennbar. Mit der Verwandlung der diskontinuierlichen Zahlenreihe in ein Kontinuum wird in der Tat nicht nur der antike Zahlbegriff, sondern der Begriff der antiken Welt selbst in Frage gestellt. Man versteht nun, daß nicht einmal die uns ohne Schwierigkeit vorstellbaren negativen Zahlen, geschweige denn die Null als Zahl – eine grüblerische Schöpfung von bewunderungswürdiger Energie der Entsinnlichung, welche für die indische Seele, die sie als Grundlage des Positionssystems der Ziffern konzipiert hat, geradezu den Schlüssel zum Sinn des Seins bildet – in der antiken Mathematik möglich ist. Negative Größen gibt es nicht. Der Ausdruck – 2 · – 3 = + 6 ist weder anschaulich noch eine Größenvorstellung. Mit + 1 ist die Größenreihe zu Ende. In der graphischen Darstellung negativer Zahlen 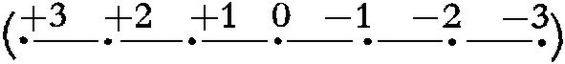werden von Null an die Strecken plötzlich positive Symbole von etwas Negativem. Sie bedeuten etwas, sie sind nichts mehr. Die Vollziehung[89] dieses Aktes lag aber nicht in der Richtung des antiken Zahlendenkens.

Alles aus antikem Wachsein Geborene ist also allein durch plastische Begrenztheit zum Range eines Wirklichen erhoben worden. Was sich nicht zeichnen läßt, ist nicht »Zahl«. Plato, Archytas und Eudoxos reden von Flächen- und Körperzahlen, wenn sie unsere zweiten und dritten Potenzen meinen, und es versteht sich von selbst, daß der Begriff höherer ganzzahliger Potenzen für sie nicht vorhanden ist. Eine Potenz vierten Grades würde aus dem plastischen Grundgefühl, das diesem Ausdruck sofort eine vierdimensionale, und zwar stoffliche Ausgedehntheit unterlegt, Unsinn sein. Ein Ausdruck gar wie e–^ix, der in unsern Formeln ständig erscheint, oder auch nur die schon im 14. Jahrhundert von Nicolas Oresme verwandte Bezeichnung 5¹/₂ wären ihnen völlig absurd erschienen. Euklid nennt die Faktoren eines Produkts Seiten (πλευραί). Man rechnet mit Brüchen – endlichen, wie sich versteht –, indem man das ganzzahlige Verhältnis zweier Strecken untersucht. Eben deshalb kann die Vorstellung von einer Zahl Null gar nicht entstehen, denn sie hat zeichnerisch keinen Sinn. Man wende nicht von der Gewöhnung unseres anders angelegten Denkens her ein, daß dies eben die »Urstufe« in der Entwicklung »der« Mathematik sei. Die antike Mathematik ist innerhalb der Welt, welche der antike Mensch um sich herum schuf, etwas Vollkommenes. Sie ist es nur nicht für uns. Die babylonische und die indische Mathematik hatten das für das antike Zahlengefühl Unsinnige längst zu wesentlichen Bestandteilen ihrer Zahlenwelten gemacht, und mancher griechische Denker wußte darum. »Die« Mathematik, es sei noch einmal gesagt, ist eine Illusion. Richtig, überzeugend, »denknotwendig« ist eine mathematische und überhaupt eine wissenschaftliche Denkweise, wenn sie vollkommen dem eigenen Lebensgefühl entspricht. Andernfalls ist sie unmöglich, verfehlt, unsinnig, oder, wie wir mit dem Hochmut historischer Geister zu sagen vorziehen, »primitiv«. Die moderne Mathematik, ein Meisterstück des abendländischen Geistes – »wahr« allerdings nur für ihn –, wäre Plato als lächerliche und mühselige Verirrung auf dem Wege erschienen, der wahren Mathematik, der[90] antiken nämlich, beizukommen; wir machen uns sicherlich kaum eine Vorstellung davon, was alles an großen Gedanken fremder Kulturen wir haben untergehen lassen, weil wir es aus unserem Denken und dessen Schranken heraus nicht assimilieren konnten oder, was dasselbe ist, weil wir es als falsch, überflüssig und sinnlos empfanden.