Kämpferdrücke, Kämpferreaktionen
[278] Kämpferdrücke, Kämpferreaktionen. Kämpferdrücke sind die Drücke, welche Bogenträger (s.d.) auf ihre Stützen, die Kämpfer, ausüben. Häufig werden auch die Reaktionen (Gegendrücke) der Kämpfer so genannt, die den Drücken auf letztere numerisch gleich, aber entgegengesetzt gerichtet sind.
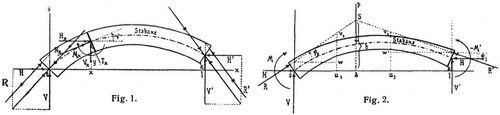
Für beliebige äußere Kräfte in der Bogenebene sind Größe und Richtung der Kämpferreaktionen R, R' durch deren Vertikalkomponenten V, V' und Horizontalkomponenten H, H' bestimmt (Fig. 1, vgl. Horizontalschub).
Bei Bogen mit Kämpfergelenken gehen R, R', abgesehen von der Reibung, durch die Gelenkmittelpunkte, während man bei stabförmigen Bogen für die Ordinaten der Schnittpunkte von R, R' mit den Vertikalen in den Achspunkten bei 0 und l hat:
w = M/H, w' = k + M'/H',
2.
worin M, M' die Angriffsmomente Mx bei 0 und l bedeuten (s. Bogen), für Bogen mit Kämpfergelenken (in der Bogenachse) sind M = M' = 0. Die Ausdrücke von V, V', H, H', M, M' hängen von der Anordnung der Bogen und den angreifenden Kräften ab. Sind alle Aktivkräfte vertikal (Lasten), dann gilt H' = H. Näheres [7], § 1. Im folgenden fassen wir besonders einfache stabförmige Bogen mit nur vertikalen Aktivkräften ins Auge, über durchlaufende Bogen und Bogenfachwerke s. [7], §§ 21–23.
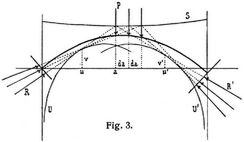
Schnittlinie der Kämpferdrücke (Kämpferdrucklinie). Auch durch eine Einzellast P werden gewisse Gegendrücke R, R' der Kämpfer hervorgerufen, welche sich mit P ins Gleichgewicht setzen, so daß P, R, R' durch einen Punkt S gehen (Fig. 2). Mit der Abszisse a der Last P ändert sich auch die Lage des Schnittpunktes S. Läßt man P nacheinander alle Lagen von a = 0 bis a = l einnehmen, so beschreibt der Punkt S eine Linie S (Fig. 3), welche Schnittlinie der Kämpferdrücke oder Kämpferdrucklinie heißt. Ihre allgemeinste Gleichung für stabförmige Bögen ist für vertikale Aktivkräfte (a Abszisse, b Ordinate):
b = (M +Va)/H,
3.
worin M, V, H einer bei a angreifenden Einzellast P entsprechen; für Bogen mit Kämpfergelenken ist M = 0. Bei symmetrisch zur Vertikalen durch die Trägermitte angeordneten Bogen liegt auch S symmetrisch zur Trägermitte. Spezielle Ausdrücke von 3. wurden unter Bogen, einfache und durchlaufende, Bogenfachwerke, Bogen mit Zugstange, Hängebrücken gegeben.
Umhüllungslinien der Kämpferdrücke. Mit der Aenderung des Angriffspunkts der Last P ändert nicht nur der Schnittpunkt S seinen Ort, sondern es geraten auch die Richtungslinien der Kämpferreaktionen R, R' in andre Lagen. Läßt man von irgend einem Angriffspunkt a aus die Abszisse a um d a wachsen, so ändern die erwähnten Richtungslinien ihre Lagen nur um unendlich wenig, wobei sich aber doch die vorige R-Linie und die neue R-Linie in einem Punkte der Koordinaten u, v schneiden (Fig. 3), und ebenso die vorige R'-Linie und die neue R'-Linie in einem Punkte der Koordinaten u', v'. Geht man wieder um da weiter, so wird die zweite R-Linie von der dritten R-Linie, die zweite R'-Linie von der dritten R'-Linie geschnitten. Fährt man so fort, so erhält man in der Verbindung der Schnittpunkte u. v aller aufeinander folgenden R-Linien eine Umhüllungslinie U der Kämpferdrücke R. Ebenso ergibt die Verbindung aller Schnittpunkte u', v' aufeinander folgender R'-Linien eine Umhüllungslinie [278] V der Kämpferdrücke R'. Für irgend eine Lage a von P sind die Koordinaten des Berührungspunkts von U (Schnittpunkts auf U):
u = (H d M – M d H)/(V d H – H d V), v = (V d M – M d V)/(V d H – H d V)
4.
und die Koordinaten des Berührungspunktes von U' (Schnittpunktes auf U'):
u' = l – [(H d M' – M' d H)/(V' d H – H d V')], v = k + (V' d M' – M' d V')/(V' d H – H d V')
5.
worin V, V', H, M, M' einer bei a angreifenden Einzellast P entsprechen und die Differentiale sich auf ein variables a beziehen. Wird mittels einer der beiden Gleichungen 4. a aus der andern eliminiert, so erhält man in der entstehenden Beziehung zwischen u und v die Gleichung der Umhüllungslinie U in gewöhnlicher Form. Unter Bogen, einfache, ist dieselbe für den wichtigsten Fall gegeben (Bd. 2, S. 160). Ebenso läßt sich aus 5. die Gleichung der Umhüllungslinie U' in gewöhnlicher Form ableiten. Dieselbe liegt für symmetrisch zur Vertikalen durch die Trägermitte angeordnete Bogen symmetrisch zur Umhüllungslinie U (vgl. Bd. 2, S. 160). Selbstverständlich kann man die Linien U, U' auch durch Auftragen einer Anzahl R-Linien bezw. R'-Linien ohne die Gleichungen von U, U' erhalten (Beispiel s. [7], S. 12). Für Bogen mit Kämpfergelenken (in der Achse) hat man bei Vernachlässigung der Reibung wegen M = M' = 0 nach 4., 5.:
u = 0, v = 0, u' = l, v' = k;
6.
die Umhüllungslinien der Kämpferdrücke sind dann Punkte, sie fallen mit den Gelenkmittelpunkten zusammen. Die im folgenden erwähnten Tangenten an die Linien U, U' sind in diesem Falle einfach Linien durch die Kämpfergelenkpunkte 0 und l.
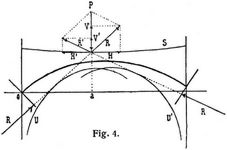
Verwendung der erwähnten Linien. Sind die Linien S, U, U' verzeichnet, so können die von einer beliebigen Last P an beliebiger Stelle a herrührenden R, R', V, V', H sehr leicht graphisch erhalten werden, wie dies in Fig. 4 angedeutet ist, während die zugehörigen M, M' aus 2. folgen. Auch die in einem beliebigen Querschnitte x durch P erzeugten Schnittkräfte ergeben sich mittels jeher Linien auf einfache Weise. Zu beachten ist dabei folgendes: In jedem Querschnitt x hängen zwei Flächen zusammen. Suchen die Kräfte und Momente links von x die Fläche daselbst von derjenigen rechts von x zu trennen, so müssen von dieser her solche Kräfte und Momente wirken, welche den ersteren numerisch gleich, aber von entgegengesetzter Richtung sind. Unter Bogen, Balken u.s.w. wurden die »Schnittkräfte« stets auf die Fläche links von x bezogen und als positiv eingeführt: die Normalkraft Nx bei Sprengbogen, wenn sie Druck bedeutet, also gegen den Querschnitt gerichtet ist (Fig. 1, 5, 6), bei Hängebögen, wenn sie, als Zug, vom Querschnitt weggerichtet ist, die Transversalkraft Tx, wenn sie von unterhalb nach oberhalb der Achsschicht wirkt, und das Moment Mx, wenn es, wie der Zeiger der Uhr, rechts um den Achspunkt des Querschnitts dreht. Es möge nun X einen Schnitt bezeichnen, welcher den Querschnitt x enthält und von dem obersten und untersten Elemente desselben senkrecht nach oben und unten geht (Fig. 5, 6). Dann ist die von P herrührende resultierende Schnittkraft im Querschnitt x, wenn P nach X angreift: Rx = R (Fig. 5), wenn P vor X angreift: Rx = R' (Fig. 6) Die entsprechenden Nx, Tx ergeben sich durch Zerlegen von Rx in Komponenten senkrecht und parallel der Ebene des Querschnitts x (Fig. 5, 6). Angriffspunkt und Richtungen von Rx, Nx, Tx, also die Vorzeichen von Nx, Tx und Mx = c Nx, sind damit ebenfalls bestimmt. Mit Rücksicht hierauf und das unter Kernlinien Gesagte konnten z.B. die unter Bogen, einfache, Bogenfachwerke, Hängebrücken gegebenen Regeln für die ungünstigsten Belastungen aufgestellt werden.
Literatur: [1] Fränkel, Berechnung eiserner Bogenbrücken, Civilingenieur 1867, S. 57 (Einführung der Kämpferdrucklinie). – [2] Winkler, Die Lehre von der Elastizität u. Festigkeit, Prag 1867, §§ 309, 312, 318, 322, 334, 336, 343 (Kämpferdruckumhüllungslinien). – [3] Müller-Breslau, Theorie und Berechnung der eisernen Bogenbrücken, I. Die stabförmigen elastischen Bogen, Berlin 1880, §§ 10, 11, 14, 15, 18, 19. – [4] Krohn, Resultate aus der Theorie des Brückenbaues, II. Bogenbrücken, Leipzig 1883, §§ 5, 6, 11, 12, 18, 19. – [5] Mantel, Der elastische Bogen unter dem Einflusse von Kräften beliebiger Richtung, Schweiz. Bauztg. 1888, II, S. 98, 111, 157, 162. – [6] Keck, Vorlesungen über Elastizitätslehre, Hannover 1893, S. 211, 232, 265. – [7] Weyrauch, Die elastischen Bogenträger, München 1897, 2, 10, 11, 15, 16, 17, 20–23; A. 2; B. 1, 13, 14, 28; S 273. – [8] Handbuch der Ingenieurwissenschaften, II. Der Brückenbau, 5. Abt., Eiserne Bogenbrücken und Hängebrücken, Leipzig 1906, S. 69.
Weyrauch.
Buchempfehlung
Holz, Arno
Die Familie Selicke
Das bahnbrechende Stück für das naturalistische Drama soll den Zuschauer »in ein Stück Leben wie durch ein Fenster« blicken lassen. Arno Holz, der »die Familie Selicke« 1889 gemeinsam mit seinem Freund Johannes Schlaf geschrieben hat, beschreibt konsequent naturalistisch, durchgehend im Dialekt der Nordberliner Arbeiterviertel, der Holz aus eigener Erfahrung sehr vertraut ist, einen Weihnachtsabend der 1890er Jahre im kleinbürgerlich-proletarischen Milieu.
58 Seiten, 4.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Geschichten aus dem Biedermeier. Neun Erzählungen
Biedermeier - das klingt in heutigen Ohren nach langweiligem Spießertum, nach geschmacklosen rosa Teetässchen in Wohnzimmern, die aussehen wie Puppenstuben und in denen es irgendwie nach »Omma« riecht. Zu Recht. Aber nicht nur. Biedermeier ist auch die Zeit einer zarten Literatur der Flucht ins Idyll, des Rückzuges ins private Glück und der Tugenden. Die Menschen im Europa nach Napoleon hatten die Nase voll von großen neuen Ideen, das aufstrebende Bürgertum forderte und entwickelte eine eigene Kunst und Kultur für sich, die unabhängig von feudaler Großmannssucht bestehen sollte. Dass das gelungen ist, zeigt Michael Holzingers Auswahl von neun Meistererzählungen aus der sogenannten Biedermeierzeit.
- Georg Büchner Lenz
- Karl Gutzkow Wally, die Zweiflerin
- Annette von Droste-Hülshoff Die Judenbuche
- Friedrich Hebbel Matteo
- Jeremias Gotthelf Elsi, die seltsame Magd
- Georg Weerth Fragment eines Romans
- Franz Grillparzer Der arme Spielmann
- Eduard Mörike Mozart auf der Reise nach Prag
- Berthold Auerbach Der Viereckig oder die amerikanische Kiste
434 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum