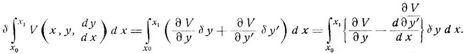Variationsrechnung
[744] Variationsrechnung, die Lehre über Maxima und Minima von Integralen, indem Funktionen gesucht werden der Art, daß gewisse Integrale einen größten oder kleinsten Wert annehmen.
Als Variationen bezeichnet man die Aenderungen, welche die Veränderlichen, Funktionen, Integrale u.s.w. erleiden, wenn an Stelle der gesuchten Funktionen, welche den Zusammenhang der abhängigen Veränderlichen von den unabhängigen angeben, andre unendlich wenig von ihnen verschiedene Funktionen treten. Es soll z.B. y als Funktion von x derart bestimmt[744] werden, daß das Integral
zu einem Maximum oder Minimum wird. Dabei ist V eine gegebene Funktion von x, y und d y/d x = y' Die Variation des Integrals ist
Hier sind δ y und δ y' die Variationen von y und y'. Soll das Integral ein Maximum oder Minimum sein, so muß
sein, wodurch sich y in Funktion von x bestimmt. Sind die Grenzen x0 und x1 sowie die zugehörigen Werte y0 und y1 nicht konstant, so treten hierzu noch gewisse Grenzbedingungen. Nach Poisson kann man die Untersuchung der letzteren umgehen, indem man nach Bestimmung von y in Funktion von x die Aufgabe als gewöhnliches Maximum- oder Minimumproblem weiter behandelt und hierdurch die Integrationskonstanten bestimmt. Bei den isoperimetrischen Problemen ist noch eine Nebenbedingung in Gestalt eines bestimmten Integrals zwischen denselben Grenzen
gegeben. Alsdann ist in die Gleichung
an Stelle von V die Funktion V + λ V1 einzusetzen. λ ist dabei eine Konstante, die sich später aus der Nebenbedingung bestimmt. Liegen mehrere abhängige Veränderliche vor, so daß
zu einem Maximum oder Minimum zu machen ist, so hat man zur Bestimmung von y, z ... die Gleichungen
Besteht hierbei noch eine Nebenbedingung in Gestalt einer gewöhnlichen oder Differentialgleichung V1 (x y y' z z' ...) = 0, so ist an Stelle von V zu setzen V + λ V1. In diesem Falle in k nicht eine Konstante, sondern eine Funktion von x. Kommen in V höhere Ableitungen y'' y''' ... vor, so bestimmt sich y aus:
Kommen in V außer der abhängigen Veränderlichen z noch zwei unabhängige x und y vor und das Integral ist ein Doppelintegral nach x und y:
so ergibt sich z aus:
Die zweite Variation gibt Aufschluß, ob Maximum oder Minimum vorliegt,
Literatur: [1] Moigno-Lindelöf, Calcul des variations, Paris 1861. – [2] Jellet, J.H., Grundlehren der Variationsrechnung, bearbeitet von Schnuse, Braunschweig 1860. – [3] Todhunter, Researches in the calculus of variations, London 1871. – [4] Dienger, Grundriß der Variationsrechnung, Braunschweig 1867. – [5] Abhandlungen über Variationsrechnung (Verfasser: Johann und Jakob Bernouilli, Euler, Lagrange, Legendre, Jacobi), herausgegeben von P. Stäckel, Bd. 1 und 2, Leipzig 1894. – [6] Zermelo, Untersuchungen zur Variationsrechnung Diss., Berlin 1894. – [7] Carll, L.B., Treatise on the calculus of variations, London 1885. – [8] Kneser, A., Lehrbuch der Variationsrechnung, Braunschweig 1900. – [9] Pascal, E., Die Variationsrechnung, deutsch von Schöpp, Leipzig 1899. – [10] Bolza, O., Vorlesungen über Variationsrechnung, I, Leipzig 1908.
Wölffing.
Buchempfehlung
Musset, Alfred de
Gamiani oder zwei tolle Nächte / Rolla
»Fanni war noch jung und unschuldigen Herzens. Ich glaubte daher, sie würde an Gamiani nur mit Entsetzen und Abscheu zurückdenken. Ich überhäufte sie mit Liebe und Zärtlichkeit und erwies ihr verschwenderisch die süßesten und berauschendsten Liebkosungen. Zuweilen tötete ich sie fast in wollüstigen Entzückungen, in der Hoffnung, sie würde fortan von keiner anderen Leidenschaft mehr wissen wollen, als von jener natürlichen, die die beiden Geschlechter in den Wonnen der Sinne und der Seele vereint. Aber ach! ich täuschte mich. Fannis Phantasie war geweckt worden – und zur Höhe dieser Phantasie vermochten alle unsere Liebesfreuden sich nicht zu erheben. Nichts kam in Fannis Augen den Verzückungen ihrer Freundin gleich. Unsere glorreichsten Liebestaten schienen ihr kalte Liebkosungen im Vergleich mit den wilden Rasereien, die sie in jener verhängnisvollen Nacht kennen gelernt hatte.«
72 Seiten, 4.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Große Erzählungen der Frühromantik
1799 schreibt Novalis seinen Heinrich von Ofterdingen und schafft mit der blauen Blume, nach der der Jüngling sich sehnt, das Symbol einer der wirkungsmächtigsten Epochen unseres Kulturkreises. Ricarda Huch wird dazu viel später bemerken: »Die blaue Blume ist aber das, was jeder sucht, ohne es selbst zu wissen, nenne man es nun Gott, Ewigkeit oder Liebe.« Diese und fünf weitere große Erzählungen der Frühromantik hat Michael Holzinger für diese Leseausgabe ausgewählt.
- Ludwig Tieck Peter Lebrecht
- Karoline von Günderrode Geschichte eines Braminen
- Novalis Heinrich von Ofterdingen
- Friedrich Schlegel Lucinde
- Jean Paul Des Luftschiffers Giannozzo Seebuch
- Novalis Die Lehrlinge zu Sais
396 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum