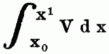Online-Bibliothek

Variationsrechnung

[363] Variationsrechnung. Wenn y = φ (x) eine Function von x von gegebener Form ist, so lehrt die Differentialrechnung das Verhältniß zu bestimmen, nach welchem sich die Function y ändert, während die unabhängig Veränderliche x um eine unendlich kleine Größe zunimmt u. bezeichnet diesen sogenannten ersten Differentialquotienten durch ^dy/_dx od. y', ferner auch das Verhältniß, nach welchem sich dieses y' bei unendlich kleiner Zunahme von x ändert u. bezeichnet letzteres durch

od. y'' etc. Es sei nun

ein bestimmtes zwischen den Grenzen x = x₀, u. x = x₁ genommenes Integral, wo V ein Ausdruck sei, welcher außer x noch eine od. mehre Functionen von x, z.B. y = φ (x), z = ψ, (x), .. u. deren Differentialquotienten y', y'', .. z', z'' .. enthalte, so kann die Frage entstehen, nach welchem Verhältniß der Werth dieses Integrals sich ändere, während sich die Form der Functionen φ (x), ψ, (x), .. ändert. Soll nun zur Beantwortung dieser Frage ein geordneter Algorithmus dienen, so muß vor allen Dingen die Änderung des Integrals eine stetige sein, so daß zwischen den, Grenzen x₀ u. x₁ überall einer unendlich kleinen Änderung der Functionen y, z, .. eine unendlich kleine Änderung des Integrals entspricht. Während nun d x, d y, .. die zusammengehörigen Zunahmen der veränderlichen Größen beim Übergang von einem Werthe x zu den benachbarten innerhalb derselben Form der Function bedeuten, so hat man für die unendlich kleinen Veränderungen von y, z, .. ∫V d x, welche von einem Übergange zu der benachbarten Form der Function herrühren, die Bezeichnung dy, dz.. ∫dx dV u. den Namen Variationen eingeführt. Die Art, diese Variationen zu bilden, erfolgt genau nach den Regeln der Differentialrechnung u. wenn, was der gewöhnliche Fall ist, gefragt wird, für welche Form der Functionen φ (x), ψ (x).. das betreffende Integral seinen größten od. kleinsten Werth annimmt, so läßt man die veränderlichen Größen, von denen das Integral abhängt, variiren, setzt in der Entwicklung des Werthes, welchen das Integral dadurch annimmt, dasjenige Glied = 0, welches die ersten Potenzen dieser Variationen enthält u. entscheidet durch die Betrachtung desjenigen Gliedes, welches die zweiten Potenzen der Variationen enthält, ob ein Minimum od. Maximum od. keins von beiden stattfindet. Der wesentliche Unterschied im Vergleich zur Differentialrechnung besteht nur darin, daß wegen des Übergangs zu einer neuen Form der Function die Variationen der Differentialquotienten dy', dy'', dz' dz'', .. ganz unabhängig von den Variationen der Größe y selbst sind, wodurch in jedem speciellen [363] Falle die Untersuchung eine weit complicirtere wird. Die V. lehrt z.B., daß unter allen Curven, welche durch zwei feste Punkte gelegt sind, die Kettenlinie diejenige ist, welche bei der Umdrehung um die Abscissenachse die kleinste Rotationsfläche erzeugt, daß die Linie, in welcher ein schwerer Punkt in der kürzesten Zeit von A nach B gelangt, wenn die Punkte A u. B weder in einerlei Vertical-, noch Horizontallinie liegen, eine Cykloide ist, welche bei horizontaler Grundlinie ihren Anfangspunkt in A, ihren Scheitel in B hat u. in der durch A u. B gelegten Verticalebene liegt, weshalb die Cykloide auch die Brachistochrone genannt wird. Die Auflösung der letzteren Aufgabe hat den ersten Anstoß zur Entwickelung der V. gegeben. Sie wurde von Johann Bernoulli gegeben. Vgl. Dirksen, Analystische Darstellung der V., Berl. 1823; Ohm, Die Lehre vom Größten u. Kleinsten, ebd. 1825; Abhandlungen von Gergonne u. Ampère im 13. u. 16. Band von Gergonne's, Annales des mathématiques, von Gourief im 13. Bd. der Nov. Act. Petrop.