|
Zwölftes Kapitel.
Die Farbenlehre.
[352] Anfänge. Wenn ich mir meine frühesten Kindheitserinnerungen zu vergegenwärtigen suche, so habe ich immer bunte Anschauungen vor mir, deren Farben ich so deutlich sehe, daß ich sie malen könnte. Dies bezeugt die starke Bevorzugung, welche das Farbenerlebnis in meinem Gehirn erfährt.
Die knappen Jugendjahre nötigten mich, die Mittel zu der erwünschten Beschäftigung mit Farben selbst herzustellen. So wurde ich mit den Farbstoffen und ihrer Herrichtung zum Malen früh vertraut. Diese nahe Bekanntschaft blieb bestehen, als ich später in dem Malen nach der Natur nicht nur eine reich fließende Quelle von Freuden fand, sondern auch ein höchst wirksames Mittel, für meinen damaligen Lebenszweck, die wissenschaftliche Arbeit in der Chemie, meinen Energiehaushalt im Gleichgewicht zu halten, trotz der großen Ausgaben nach jener Richtung. Es ist natürlich, daß ich meine Wissenschaft gelegentlich auch auf die technische Seite jener Liebhaberei anwandte und dabei mancherlei Brauchbares fand.
So lebhaft mich gelegentlich derartige Fragen erfaßten, hielt ich mich doch lange Zeit nicht für berechtigt, sie zum Gegenstand ernsthafter Forschung zu machen. Erst als ich durch die Wendung zur Naturphilosophie[353] die Wälle meines bisherigen Arbeitsgebietes durchbrochen hatte, fand ich den Mut, auch die anderen, bisher zurückgedrängten Triebe sich entfalten zu lassen und die Technik des Forschens, die ich an den chemischen Aufgaben erlernt und geübt hatte, auch auf solche Gebiete anzuwenden.
Maltechnisches. Der erste Vorstoß hing natürlich noch eng mit der Chemie zusammen. Gegen Ende des 19. Jahrhunderts traten die üblen Folgen zutage, welche durch die ausschließlich idealistisch-ästhetische Ausbildungsweise der Künstler notwendig hervorgerufen werden mußten. Fast niemand verstand in diesen Kreisen mehr etwas von der chemisch-technischen Seite der Malerei, nicht einmal etwas von der einfach handwerklichen, so daß die ohne jede Kenntnis der Daseinsbedingungen hingestrichenen Ölgemälde rettungslos verfielen, kaum daß sie die Werkstatt des Erzeugers verlassen hatten. Ein sonst so gewissenhafter Künstler wie Menzel untermalte seine Ölbilder mit Florentinerlack, ohne zu wissen, daß dieser ungefähr der niederträchtigste Reißer ist, den es gibt. Oder vielmehr gab, denn man ist jetzt endlich dahinter gekommen und hat ihn aufgegeben. So hatten sich seine früheren Werke schon nach wenigen Jahren mit einem Netz von Sprüngen bedeckt, die sich unaufhaltsam vermehrten. Böcklin experimentierte in ganz alchymistischer Weise ohne jede wissenschaftliche Grundlage. Vielmehr entnahm er seine Anregungen den unklaren Andeutungen alter Schriftsteller, die er im Besitz übernatürlicher Malerweisheit glaubte. So verfuhren auch die anderen, die damals sich mit solchen Fragen abgaben. Statt die vorhandene chemische Wissenschaft zu Rate zu ziehen, deren Wirksamkeit Pettenkofer gelegentlich erwiesen hatte, zankten sie sich über die Auslegung alter Texte von Autoren, die meist nicht aus eigener Kenntnis, sondern vom Hörensagen berichtet hatten. Die Fabriken aber benutzten gelegentlich die Unwissenheit[354] der Künstler, um ihnen wertloses Material anzuhängen, wozu die eben entdeckten Teerfarbstoffe reichliche Gelegenheit boten.
Es entstand auch in der damals führenden Kunststadt München ein Verein, der sich die Bekämpfung dieser Übelstände zur Aufgabe setzte. Obwohl ich kein Vertrauen in seine Wirksamkeit hatte, da er größtenteils aus Künstlern bestand, die von der Sache nichts oder nicht viel verstanden, war ich doch willig, mich anzuschließen. Als ich aber die Drucksachen durchsah und Erkundigungen einzog, stellte sich folgendes heraus. Zum Führer des Vereins war der ausgezeichnete Bildnismaler Lenbach gewonnen worden. Dieser benutzte gern Asphalt zum Malen, obwohl er zu den gefährlichsten Farbstoffen gehört, da er nie völlig fest wird. Bei Lenbachs meist sehr dünnem Auftrag konnten üble Folgen nicht so leicht eintreten; in der Hand des Unerfahrenen, also der Mehrzahl aller Künstler, war er selbstmörderisch. Als ich nun die Liste der vom Verein als vollkommen zuverlässig bezeichneten »Normalfarben« durchsah, fand ich zu meinem Erstaunen auch Asphalt darauf. Ich ging der Sache nach und stellte fest, daß Lenbach die Hergabe seines Namens davon abhängig gemacht hatte, daß sein geliebter Asphalt nicht mit dem Makel der Unzuverlässigkeit behaftet werden durfte. Später, als Lenbach gestorben war, wurde der Asphalt ohne Pension abgebaut.
Ich verzichtete also lieber.
Die Malerbriefe. Durch meine Ferienmalerei hatte ich mir ausreichend praktische Erfahrungen gesammelt, um mit Erfolg meine chemisch-physikalischen Kenntnisse hier anwenden zu können. Ich schrieb eine Reihe von Aufsätzen, die zuerst in einer Münchener Zeitung, sodann in Buchform unter dem Titel »Malerbriefe« veröffentlicht wurden (1904). Aus der Tatsache, daß eine[355] Anzahl neuer Worte, die ich bei dieser Gelegenheit gebildet und ohne Hinweis auf ihre Neuheit benutzt hatte, inzwischen in den allgemeinen Gebrauch aufgenommen worden sind, kann ich erkennen, daß das Büchlein mit Nutzen gelesen worden ist. Es war bald vergriffen und ich verabsäumte leider wieder einmal, rechtzeitig für die Bearbeitung der Neuauflage zu sorgen.
In der Vorrede hatte ich geschrieben, daß ich den bisherigen antiquarisch-»philosophischen« Betrieb der Kunstwissenschaften unbefriedigend fand und an seine Stelle das wissenschaftliche Verfahren gesetzt zu sehen wünschte, nämlich das empirisch-experimentelle. Dadurch hatte ich es für mein ganzes weiteres Leben mit den Kunstschreibern verdorben und habe von dieser Seite alle Bemühungen erfahren, die es gibt, um meine Arbeiten unwirksam zu machen. Nur ganz wenige Ausnahmen habe ich erlebt, und denen ist ihr Mangel an Klassenbewußtsein nicht gut bekommen.
Als Summa meiner Erörterungen sprach ich die Forderung aus: der Künstler schaffe bewußt. Er sei sich unaufhörlich klar über den Zweck, den er eben erreichen will, und über die Mittel, mit denen er ihn erreichen kann. Und nach der Bemerkung, daß eine gleiche Entwicklung auf allen Gebieten menschlicher Arbeit nachweisbar ist, schloß ich: Auch in der Kunst hat die unbewußte Eingebung dem bewußten Können zu weichen.
Mir ist es nach bald einem Vierteljahrhundert eine angenehme Überraschung, daß ich beim Nachsehen jenes alten Büchleins den Grundgedanken schon klar ausgesprochen finde, durch welchen meine ganze spätere Kunstbetätigung bestimmt worden ist. Doch will ich auch nicht die Bemerkung unterdrücken, daß ich damals es als die Aufgabe des Malers ansah, sein Werk so[356] zu gestalten, daß es beim Betrachten dieselben psychophysischen Empfindungen hervorruft, wie die Natur. Dies ist ein grundsätzlicher Irrtum. Ich hatte ihn von Helmholtz übernommen, der ihn als selbstverständliche Forderung in seinem berühmten Vortrage: Optisches über Malerei ausgesprochen hatte, und er lag dem damals herrschenden Impressionismus zugrunde. Ich habe schon früher (II, 190) auf die unüberwindbaren inneren Schwierigkeiten hingedeutet, in welche ich durch die ungeprüfte Annahme jener Selbstverständlichkeit geriet. Erst durch die Schaffung der messenden Farbenlehre und der auf ihr begründeten gesetzlichen Farbharmonik wurde ich in den Stand gesetzt, mich daraus zu befreien. Und nachträglich kann ich auch einsehen, warum weder Helmholtz noch ich vermocht hatte, damals den Irrtum als solchen zu erkennen. Es war eben der Mangel an Zahl und Maß in der Farbenwelt.
Diese Untersuchungen führten mich weiter zur Entwicklung der Pastelltechnik als der von den Nachteilen der Bindemittel freiesten und gaben mir Anlaß, manche meiner Reiseskizzen zu größeren Bildern auszugestalten, die einen guten Eindruck auf die Beschauer erzeugten, so daß ich viele davon an Freunde und Angehörige verschenkte. Ein lieber Freund freute sich über eine solche Gabe dermaßen, daß er mir sagte: Du, wann i so malen konnt, i tät überhaupt den ganzen Tag nix andres. Damals lachte ich darüber; später habe ich mich immer dringender gefragt, ob er nicht eigentlich Recht hatte. Und nun habe ich mich endgültig entschlossen, nach der Beendigung dieses Buches ganz und gar Maler zu werden, und freue mich schon ganz unbändig darauf, wenngleich ich weiß, daß es wahrscheinlich zu spät sein wird. Vielleicht wird aber ein Teil der Jugend, die dem Künstler mangelt, durch die Jugend der führenden Gedanken ersetzt werden können.
[357] Das Problem der Farbordnung. Auf den nachfolgenden Seiten gedenke ich die Einzelheiten meiner Arbeiten an der Farbenlehre eingehender zu schildern, als dies bei den früheren Berichten über andere Arbeiten geschehen ist, und zwar aus mehrfachen Gründen. Subjektiv bin ich der Meinung, daß in diesen Arbeiten sich die Besonderheiten am deutlichsten aussprechen, welche mein Gehirn von den anderen gleichen und besseren unterscheiden und daß sie somit den Höhepunkt meiner wissenschaftlichen Leistungen darstellen. Objektiv darf der Gegenstand eine ganz allgemeine Teilnahme beanspruchen, denn Farben sind es, was wir unmittelbar mit dem Auge, dem bei weitem wichtigsten Sinnesorgan wahrnehmen. Die Formen, Gestalten, Dinge, die wir zu sehen glauben, ergeben sich erst aus der Deutung der Farbflecken, welche das Gesichtsfeld des sehenden Auges erfüllen.
Und was den Leser persönlich betrifft, so braucht er eben deshalb nicht zu fürchten, daß die folgenden Darlegungen ihn in unzugängliche Gebiete abstrakter Wissenschaft drängen werden. Was kann es anschaulicheres geben, als das, was unser Auge beständig erfüllt, die Farbe? Und wenn er weiter gewahr wird, welche unerwarteten kulturellen Folgen von unabsehbarer Auswirkung notwendig aus diesen Untersuchungen entstehen müssen und werden, so würde er mit Recht dem Verfasser Vorwürfe machen können, wenn dieser ihm nicht einen Blick in das Wachsen und Wesen solcher Dinge gegönnt hätte.
Endlich ist es hier möglich, an einem geschlossenen Beispiel aufzuzeigen, wie ein neues wissenschaftliches Feld geordnet und urbar gemacht wird. Da alles aus einer Hand hervorgegangen ist, treten die Zusammenhänge besonders deutlich zutage und man kann das Ganze als eine Anleitung zum Entdecken ansehen. Da es sich hierbei um ganz elementare Verhältnisse handelt,[358] sind die erforderlichen Gedanken und Begriffe so einfacher Art, daß sie jedermann zugänglich sind. Habe ich doch oft Gelegenheit gehabt, zu sehen, wie leicht und gern sich Kinder die Grundbegriffe der neuen Farbenlehre aneignen. Nur nicht wenige Künstler behaupten, daß sie sie nicht zu Kopf bringen können.
Auf dem früheren primitiven Standpunkte des Landschaftsmalers wäre ich vielleicht stehen geblieben, wenn nicht von ganz anderer Seite eine neue Anregung eingetreten wäre. In unserem reichen Brückenprogramm befand sich unter anderem auch die Ordnung und Normung der Farben (III, 299). Diese Aufgabe war schon vorher vom Deutschen Werkbund ins Auge gefaßt und zu lösen versucht worden, indem alle bekannten Ansätze dazu einem Ausschuß vorgelegt wurden, meist von den Erfindern oder ihren Beauftragten. Doch wurde kein praktisch brauchbares Ergebnis erzielt. Ich hatte mich etwa im Jahr 1912 dem Werkbund angeschlossen und auch eine Tätigkeit im Ausschuß angenommen, obwohl mir mancherlei an seinem Vorgehen nicht gefiel. Um nun nicht doppelte Arbeit zu machen oder zu veranlassen, schlug ich dem Werkbunde eine gemeinsame Weiterarbeit vor, die auch von diesem auf seiner Kölner Tagung im Unglücksjahr 1914 beschlossen wurde.
Ich hatte mich bis dahin nicht sehr eingehend mit der Frage beschäftigt, obwohl ich seinerzeit eine besondere Anregung dazu empfangen hatte. Während meines Aufenthalts in Cambridge war ich in Boston mit A.H. Munsell zusammengetroffen, der mir seine nach solcher Richtung angestellten Arbeiten zeigte (III, 63). Ich habe schon berichtet, daß und warum ich seine Lösung nicht für zureichend ansehen konnte. Da er aber eine wirkliche, wenn auch unvollkommene Farbordnung erzielt hatte, traute ich mir nun zu, selbst den Weg zu finden, um die Aufgabe befriedigend zu lösen, zumal ich bereits[359] früher mit der experimentellen Bearbeitung der Angelegenheit begonnen hatte. Zunächst natürlich auf der von Helmholtz gegebenen und von niemand, auch von mir nicht bezweifelten Grundlage, daß Farbton, Reinheit und Helligkeit die drei Elemente sämtlicher Farben seien.
So ist mir noch erinnerlich, wie ich auf der Rückreise von London im Frühling 1914 allein auf dem Kanaldampfer saß und mir den Kopf zerbrach, wie ich mit diesen Veränderlichen den Farbkörper aufbauen sollte. Denn so viel war zweifellos: die verschiedenen reinen Farben haben nicht etwa gleiche Helligkeit, sondern sehr verschiedene. Schon Goethe hat immer wieder hervorgehoben, das Gelb die hellste, dagegen Blau die dunkelste Farbe sei und seitdem waren eine Anzahl Messungen über die Eigenhelligkeit der verschiedenen reinen Farben gemacht worden, die dasselbe ergaben, wenn auch mit abweichenden Zahlenwerten. Munsell hatte dies dadurch auszudrücken versucht, daß er die von Runge gegebene Anordnung aller Farben in einer Kugel übernahm, aber den Kreis der reinen Farben nicht in den Äquator legte, sondern in eine schräge Ekliptiklinie. Das war methodisch unmöglich, da die Linie der reinen Farben überall den größten Abstand von der Achse haben muß. Aber ohne Modell vermochte ich mir nicht vorzustellen, was aus der Kugel bei richtiger Umgestaltung wurde.
Zu Hause setzte ich die Arbeit am Modell fort, fand aber so verwickelte Verhältnisse, daß ich zu der Überzeugung kam, auf diesem Wege nichts erreichen zu können.
Eigene Arbeiten. Grau. Bald darauf brach der Weltkrieg los. Ich habe schon dargelegt, wie alle internationalen Beziehungen, die bisher den größten Teil meiner Beschäftigungen ausgemacht hatten, abgerissen waren. Ich war 61 Jahre alt, war also über jede Möglichkeit aktiver Betätigung hinaus. Mein Angebot freiwilliger[360] Mitarbeit wurde nicht berücksichtigt. So blieb mir nichts übrig, als eine Vertiefung in die vorliegende wissenschaftliche Arbeit, die um so eher eine ausreichende Beanspruchung in Aussicht stellte, als ich offenbar die vorhandenen Schwierigkeiten sehr unterschätzt hatte.
Da ich kurze Zeit vorher für mein Buch »Moderne Naturphilosophie« die Grundlagen der Ordnungslehre bearbeitet und dargestellt hatte, sah ich hier eine Gelegenheit vor mir, dies gewaltige Arbeitsmittel bewußt anzuwenden. Das erste Ergebnis war, daß die Arbeit geteilt werden mußte. Zunächst war der einfachere Fall der Graureihe mit den Endpunkten Weiß und Schwarz aufzuklären. Wenn man die heutige Darstellung, z.B. in meiner »Farbfibel« liest, so kann man sich nicht vorstellen, welche Denkschwierigkeiten hier zu überwinden waren. Der vorgeschrittenste Farbforscher jener Zeit, E. Hering, wußte nichts vom vollkommenen Weiß. In seiner »Lehre vom Lichtsinn«, der ich sehr viel verdanke, fehlte der schon vor mehr als einem Jahrhundert durch Lambert eingeführte Begriff der Weiße (albedo) ganz, und dadurch war er verhindert, selbst über die einfache Gruppe der »unbunten« Farben klar zu werden. Unter anderem verwechselte er Spiegelung mit Weiße. Wenn ich nicht zufällig in meiner Rigaer Zeit die Schriften des Astrophysikers F. Zöllner gelesen hätte, in denen viel von der Albedo des Mondes die Rede ist, so wäre ich möglicherweise schon in diesem Loch stecken geblieben. So konnte ich es vermeiden, und dadurch ist mir der Spiritismus, dem Zöllner verfallen war, und wegen dessen seine Schriften damals sehr verbreitet waren, von unerwartetem Nutzen gewesen.
Eine andere Frage, auf die ich in der Literatur keine Antwort gefunden hatte, war die: wie sieht reines Grau aus? Daß Mischungen von weißen und schwarzen Farbstoffen bläuliche Graufarben ergeben, war bekannt,[361] ebenso die Ursache hierfür. Nun zeigt die Theorie verschiedene Möglichkeiten, auf optischem Wege reines Grau erscheinen zu lassen und es mit jenen Mischungen zu vergleichen. Das Ergebnis war zunächst eine Vorschrift, nach welcher man Kreide, Ruß und gelben Ocker mischen muß, damit das Produkt neutral grau aussieht. Mir ist die Überraschung und Freude im Gedächtnis geblieben, mit welcher ein befreundeter sehr erfahrener Mitarbeiter auf dem Farbgebiet die ersten Blätter begrüßte, die mit neutralem Grau angestrichen waren. Dieses war ihm wie allen Anderen bis dahin unbekannt gewesen.
Einführung von Maß und Zahl. Nun entstand die Aufgabe, die verschieden hellen Graustufen zu messen. Zuerst machte ich es wie üblich mit dem Farbkreisel durch Mischung von Weiß und Schwarz mittels Scheiben. Aber da wußte ich, daß jedes Weiß etwas Schwarz enthält, und ebenso jedes Schwarz etwas Weiß; und diese kann man nicht mit dem Kreisel messen. Ich erfand deshalb das Halbschatten-Photometer (Hasch), mit dem ich wenigstens reines Schwarz machen konnte, indem ich das Licht ganz ausschloß. Und die verschiedenen weißen Aufstriche oder Pulver konnte ich damit vergleichsweise auf ihre Weiße messen.
Es ergab sich, daß die untersuchten weißen Pulver alle einer gewissen Grenze nahe, also fast rein weiß waren. Unter ihnen waren einige wenige am weißesten und untereinander gleich; diese durften daher als praktisch rein weiß oder schwarzfrei angesehen werden. Am leichtesten ließ sich von ihnen reines Bariumsulfat herstellen; dies ergab also das reine oder normale Weiß.
Nun hatte ich die Möglichkeit an der Hand, jedes Grau zu messen. Denn mein Hasch erlaubte mir, die Beleuchtung des Normalweiß in gemessener Weise zu vermindern und es so dem vorgelegten Grau gleich aussehend[362] zu machen. War dies erreicht, so wußte ich, welcher Bruchteil des auffallenden Lichts vom Grau zurückgeworfen wurde, nämlich derselbe Bruchteil, den das Weiß im Hasch empfing. Und damit war das Grau gemessen, denn dieser Bruch bezeichnete es eindeutig. Jede andere graue Farbe, welche den gleichen Bruchteil Weiß enthält, ist jener gleich. Wirft sie mehr Licht zurück, so ist sie heller, im anderen Falle dunkler, als jenes Grau. So war ich in der Lage, beliebige Stufen Grau herzustellen. Ich machte alsbald solche mit ein Zehntel, zwei Zehntel, drei Zehntel, vier Zehntel usw. bis neun Zehntel Schwarz und erwartete eine schöne Stufenreihe.
Sie war es keineswegs. Die ersten Stufen: ein Zehntel, zwei Zehntel, drei Zehntel sahen gar nicht grau aus, sondern weiß; erst bei vier Zehntel oder fünf Zehntel, konnte man von einem deutlichen Grau sprechen. Und gegen Ende, sieben Zehntel, acht Zehntel, neun Zehntel, waren es nicht Stufen, sondern Sprünge. Auch war neun Zehntel noch sehr weit von Schwarz entfernt, unvergleichlich viel weiter, als ein Zehntel von Weiß.
Nun kam mir die Erinnerung an Fechners Elemente der Psychophysik, ein Buch, das ich auch schon in Riga ohne anderen Grund gelesen hatte, als weil mich der Gedanke einer messenden Seelenlehre so stark gefesselt hatte, daß ich wissen mußte, was daran war. Und in Leipzig war ich durch die persönliche Begegnung mit Fechner (II, 96) und hernach durch den Verkehr mit Wundt, der Fechners Gedanken eine weite Entwicklung gegeben hatte, wiederholt zur Beschäftigung mit der Psychophysik veranlaßt worden. Wieder hatte ein solches zielloses Kennenlernen eines fernliegenden Gebietes aus bloßer wissenschaftlicher Neugier sich als eine reichlich zinstragende geistige Kapitalanlage erwiesen.[363]
Denn ich sah sofort, daß hier das von Weber zuerst ausgesprochene, von Fechner aber erst seiner Bedeutung gemäß entwickelte Gesetz wirksam war, wonach die Reize in geometrischer Reihe oder nach gleichem Verhältnis abnehmen müssen, damit die Empfindungen eine gleichabständige oder arithmetische Reihe bilden. Als Reiz war hier der Anteil Weiß wirksam.
Hiernach stellte ich eine Reihe grauer Farben her, deren Weißanteile eine geometrische Reihe bildeten oder in gleichem Verhältnis abnahmen, und hatte die Genugtuung, die gesuchte gleichstufige Grauleiter vor mir zu sehen. Indem ich zwischen zwei Pappstreifen die abgestuften grauen Sprossen wie bei einer wirklichen Leiter anbrachte, konnte ich die Leiter auf eine beliebige graue Fläche legen und augenblicks die Sprosse erkennen, die dasselbe Grau zeigte, wie die zwischen den Sprossen hervorschauende Unterlage. Auf solche Weise konnte ich also unbekannte graue Farben ebenso leicht und schnell messen, wie man unbekannte Längen mit einem eingeteilten Maßstabe mißt.
So einfach diese Dinge sind, so neu waren sie damals. Hunderte und Tausende von messenden Versuchen über graue Farben waren angestellt worden, seit Maxwell 60 Jahre vorher gezeigt hatte, wie man Farben mittels des Farbkreisels messend vergleichen kann. Aber niemand hatte sich die Frage gestellt und beantwortet, ob man nicht die Messungen auf absolutes Weiß und Schwarz beziehen könne. Das absolute Schwarz war sogar den Physiologen und Psychophysikern bekannt, da man es sieht, wenn man in einen innen schwarz getünchten Kasten eine Öffnung macht. Nur das absolute Weiß mußte noch gefunden und dann die Einteilung gemäß dem Fechnerschen Gesetz durchgeführt werden. Freilich gehörte dazu ein Arbeiter, der sich mittels der Ordnungswissenschaft die hier vorliegenden Aufgaben und die[364] möglichen Wege zu ihrer Erledigung grundsätzlich klar gemacht hatte. Und solcher gab und gibt es noch nicht viele.
Das Fechnersche Gesetz. Wie man gesehen hat, beruht die Normung der unbunten Farben auf der Anwendung des Fechnerschen Gesetzes. Dieses war schon 1859 auf Grund der noch älteren Arbeiten Webers ausgesprochen worden und hat sich seitdem allseitig als Grundgesetz der Psychophysik erwiesen. Und doch war die Festlegung der Graunormen mit Hilfe dieses Gesetzes meines Wissens der erste Fall, wo es praktisch angewendet wurde. Bis dahin hatten die Physiologen und Psychophysiker es nur benutzt, um darüber zu streiten, kleine Abweichungen davon zu Widerlegungen aufzubauschen, kurz Scholastik damit zu treiben.
Tatsächlich ist dies Gesetz grundlegend für alle Fragen, die etwas mit der Empfindung im weitesten Sinne zu tun haben. Die gegenwärtig in Richterkreisen aufdämmernde Erkenntnis, daß Strafen nach der Beschaffenheit des Verurteilten zu bemessen sind, daß z.B. eine Geldstrafe von 100 M. für einen Armen zerstörend wirken kann, während der Reiche sie kaum empfindet, wäre längst Allgemeingut geworden, wenn man nur das Fechnersche Gesetz anzuwenden gewußt hätte. Und andererseits hätte der Normenausschuß für die Deutsche Industrie sich manchen Mißgriff ersparen können, wenn er sich klar gemacht hätte, daß die Aufgabe, Normstufen gleichabständig festzustellen, durch geometrische Reihen gemäß dem Fechnerschen Gesetz gelöst werden muß, nicht aber durch arithmetische, wie es gewöhnlich geschieht.
Es ist in der Tat nicht auszusagen, wieviel Lebensweisheit man aus diesem Naturgesetz gewinnen kann. Der Ausspruch: alles ist relativ, erlangt in seinem Lichte einen ganz klaren und bestimmten Inhalt und die Selbstgewöhnung, das eigene Leben gemäß diesem[365] Gesetz zu regeln, beseitigt unzählige Härten und Widersprüche, die nicht in den Dingen liegen, sondern durch die Fehler unserer »absoluten« Denkgewohnheiten hervorgerufen werden.
Die unbunten Normen. Auf solche Weise war das Gebiet der unbunten Farben geregelt. Denn die Frage, welche von den unbegrenzt vielen geometrischen Reihen, nach denen man die Grauleiter abstufen kann, gewählt werden soll, war eindeutig in dem Augenblicke entschieden, in dem sie gestellt wurde. Da die gleichförmig fortschreitende Reihe der Zahlen durch die Bildung von Zehnergruppen geteilt und genormt ist, so muß auch jene geometrische Reihe nach der Zehnerordnung angesetzt werden, denn jede einmal festgelegte Normung muß in allen Anwendungen streng beibehalten werden. So ergibt die erste Zehnerteilung die Reihe Weiß = 1, 1/10, 1/100, 1/1000, usw. Da aber schon ein Schwarz mit 1/100 Weiß nur schwierig herzustellen ist, so sind die Sprünge viel zu weit. Es müssen also zwischen 1 und 1/10 noch 9 Stufen in geometrischer Reihe eingeschaltet werden, und ebenso viele zwischen 1/10 und 1/100. Dann haben wir 20 Stufen in dem ganzen erreichbaren Gebiet zwischen Weiß und Schwarz, und diese erweisen sich durchaus als eng genug. Für die meisten Zwecke sogar zu eng, so daß man nur jede zweite Stufe braucht.
Um diese Stufen kurz zu bezeichnen, wählte ich das gleiche Verfahren, wie die Musik: ich ordnete ihnen die Buchstaben des ABC zu, so daß a Weiß bedeutet, b, c, d usw. helles Grau, das stufenweise dunkler wird. g, h, i sind mittlere Grau, k, l, m sind dunkelgrau bis zur Grenze des Schwarz, n bis t werden schon Schwarz genannt. Auf Papier kommt man meist nicht über p hinaus, das die Farbe guter Druckerschwärze ist. Läßt man, wie erwähnt, jede zweite Stufe aus, so hat man die Graureihe[366] a, c, e, g, i, l, n, p für die täglich vorkommenden Graunormen.
Dies sind in großen Zügen die Ergebnisse meiner Überlegungen und Versuche über die Frage, wie die Reihe der unbunten Farben zu normen sei. Sie wurden keineswegs mit einem Schritt erreicht, sondern ich hatte einige andere Ordnungen vorher versucht, die mir zufällig näher lagen. Doch besann ich mich rechtzeitig auf die Erfahrung, daß in grundlegenden Dingen kein Fremdkörper geduldet werden darf. Denn er erweist sich ganz sicher auf die Dauer als unerträglich. Und je später er abgestoßen wird, um so schwieriger und kostspieliger wird diese Notwendigkeit, weil so viel mehr, was damit zusammenhängt, umgestellt werden muß. Darum sind beispielsweise die natürlichen Sprachen so unvollkommen, weil sie festgelegt (genormt) wurden zu einer Zeit, wo noch gar keine Klarheit über die logischen und technischen Erfordernisse an eine gute und zweckmäßige Sprache bestand. Und darum schleppen wir uns heute noch mit einem Kalender von grotesker Unsinnigkeit, in welchem die Maßeinheit des Monates von 28 bis zu 31 Tagen schwankt, also um 10 v.H. ihres Wertes, der unveränderlich sein sollte.
Fremdkörper in solchem Sinne aber sind alle willkürlichen Annahmen, wo die Dinge schon durch eine ältere fundamentale Normung (wie hier die Zehnerzählung) festgelegt sind. Erst nachdem alle solche Willkür aus den Normen für die unbunte Reihe ausgeschieden war, konnte ich meine Aufgabe als beendet ansehen. Dafür ist denn auch das Ergebnis von entsprechender Dauerhaftigkeit. Mehr als zehn Jahre sind diese Normen von mir und meinen Mitarbeitern in der mannigfaltigsten Weise benutzt worden, und niemals hat sich eine Notwendigkeit, ja nicht einmal ein Wunsch ergeben, sie zu[367] ändern. Ebensowenig ist von gegnerischer Seite etwas gegen sie vorgebracht worden.
Die einzige absehbare Verbesserung, welche sie vielleicht in Zukunft erfahren werden, wird eintreten, wenn die Zehnerzählung durch die viel zweckmäßigere Zwölferzählung (zwölf läßt sich durch 2, 3, 4, 6 teilen, 10 nur durch 2 und 5) ersetzt sein wird. Aber bis die Welt so weit organisiert sein wird, werden voraussichtlich noch einige Jahrhunderte vergehen müssen.
Messung der Buntfarben. So war ich schließlich mit den unbunten Farben in Ordnung gekommen. Ich muß bekennen, daß es einige Selbstüberwindung gekostet hatte, mich nicht gleich Hals über Kopf in das reizvolle Gewimmel der Buntfarben zu stürzen. Aber da die unbunten die einfacheren sind, so wäre es grobe Energievergeudung gewesen, vor Lösung der leichteren Aufgabe an die schwerere zu gehen. Und da von meinen Vorgängern keiner versucht hatte, im grauen Gebiet endgültige Ordnung zu schaffen, so war es ganz erklärlich, daß das im bunten erst recht nicht gelingen konnte.
Daß ich dergestalt meine Gefühle durch wissenschaftliche Betrachtungen regelte, hat sich dann in der Folge als im höchsten Maße segensreich erwiesen. Beim Rückblick auf die mühsame Kletterarbeit, die mich auf die inzwischen erreichten Höhen geführt hat, kann ich feststellen, daß jener graue Weg sich tatsächlich als der einzige erwiesen hat, auf dem ein Zugang möglich war. Denn die hier entwickelten Denkmittel waren unentbehrlich zur Lösung der schwierigeren Aufgaben im bunten Gebiet.
Ein hellgraues Papier wird als solches gesehen und beurteilt, ob das Licht; in dem wir es betrachten, stark oder schwach ist, ob das Papier also viel oder wenig Licht zurückschickt. Damit wir aber das Urteil: hellgrau fällen, ist es notwendig, daß wir das Papier innerhalb[368] einer Umgebung sehen, deren Lichtverhältnisse uns bekannt sind und somit seine Farbe auf die der bekannten Gegenstände beziehen können. Denn schließen wir diese durch ein innen geschwärztes Sehrohr mit engem Gesichtsfelde aus, in welchem man nur das graue Papier sieht, so wird unser Urteil unsicher und unbestimmt. Das gleichförmig erhellte leere Gesichtsfeld eines Mikroskops ohne Gegenstand vor der Linse wird nicht grau, wenn wir etwa durch Schließen der Blende am Beleuchter das Licht vermindern, sondern bleibt unbezogen jenseits von Weiß und Grau.
Diese und viele ähnliche Beobachtungen, zum Teil von sehr auffallender Beschaffenheit hat E. Hering zusammengestellt aber nicht unter einen gemeinsamen Gesichtspunkt gebracht oder in ihrer Gesetzlichkeit erkannt, die durch die Worte bezogen und unbezogen gedeutet wird. Dies lag in erster Linie daran, daß ihm Lamberts Begriff der Weiße oder Albedo fremdgeblieben war. Er kannte keine weißeste Fläche, sondern glaubte, daß die Weiße unbegrenzt wachsen könne.
Ich hatte hart zu ringen, um mich von diesem Irrtum des aufrichtig verehrten Kollegen (er lebte damals noch und ich stand mit ihm im Briefwechsel) frei zu machen. Dies gelang durch das Studium von Lamberts Photometrie, von der eine gute Bearbeitung in meinen »Klassikern der exakten Wissenschaften« (II, 55) leicht zugänglich war. Es war dies ein Fall und durchaus nicht der einzige, wo ich für die Mühe bei der Begründung der »Klassiker« reichen Lohn gewann, der sich in der Folge noch vergrößerte, wie bald erzählt werden wird. Endlich gelang es, jenen Gesichtspunkt zu gewinnen, von dem aus die große Mannigfaltigkeit jener Erscheinungen sich gesetzlich ordnen und übersehen ließ.
Bezogene und ungezogene Farben. Es handelte sich wieder um eine schöpferische Begriffsbildung, etwa wie[369] bei der Katalyse, ohne daß es nötig war, hierfür besondere Experimentaluntersuchungen auszuführen. Ich erkannte, daß die Farben in zwei Gruppen zerfallen, die bezogenen und die unbezogenen. Unbezogen sind die Farben, welche allein in einem dunklen Gesichtsfelde erscheinen. Solche Farben sieht man in den optischen Apparaten; das Spektrum ist das bekannteste Beispiel dafür. Sie heißen unbezogen, weil man sie nicht inmitten der allgemeinen Umgebung sieht, sondern für sich allein. Man weiß daher nicht, in welchem Verhältnis sie zu ihrer Lichtquelle stehen. Bei den bezogenen Farben ist alles dies umgekehrt.
Die Folgen hiervon sind merkwürdig und weitreichend. Bei den unbezogenen Farben gibt es kein Grau und Schwarz, sondern nur Weiß und Bunt. Macht man z.B. ein Spektrum durch Lichtverminderung immer dunkler, bis es verschwunden ist, so sieht man nicht Schwarz an seiner Stelle, sondern man sieht die Stelle überhaupt nicht mehr. Das ist ein großer Unterschied. Macht man es immer heller, so erscheint es zuletzt blendend weiß. Mit einem Worte: bei unbezogenen Farben gibt es kein Schwarz, sondern nur Weiß und Bunt. Schwarz und Grau treten nur bei bezogenen Farben auf.
Bezogene Farben sind die Farben der Gegenstände unserer Umgebung. Sie werden durch den Anteil bestimmt, den sie von dem auffallenden Licht zurücksenden. Wird alles zurückgesendet, so ist der Gegenstand weiß, gleichgültig ob die Beleuchtung und damit das zurückgesendete Licht stark oder schwach ist. Wird alles Licht verschluckt, so ist der Gegenstand schwarz. Wird ein Bruchteil des Lichts zurückgesendet, so ist der Gegenstand grau. Dies gilt aber nur für den Fall, daß von allen Lichtarten oder Wellenlängen der gleiche Bruchteil zurückgesendet wird. Ist das nicht der Fall, so ist der[370] Gegenstand bunt1 (rot oder gelb oder grün usw.) je nach der Lichtart, welche im zurückgesendeten Licht überwiegt. Und zwar ist die Buntfarbe um so reiner, je stärker dies Überwiegen einer bestimmten Lichtart auftritt.
Mit einem Wort: die Farben der Gegenstände unserer Umgebung oder die bezogenen Farben werden durch die Verhältnisse der Lichtzurückwerfung (Remission) der Korperoberflächen bestimmt.
Helmholtz. Man kann sich heute nur schwer vorstellen, was für ein Licht mir bei dieser Entdeckung aufging. Zunächst sah ich, daß Helmholtz, dessen Werk über physiologische Optik als ein gewaltig hoher Gipfel dieser Wissenschaft mit Recht gewertet wurde, fast nur mit unbezogenen Farben gearbeitet hatte, wie es dem Physiker ja unmittelbar nahe lag. Bei der Frage nach der Ordnung der Farben, der er nur geringe Aufmerksamkeit schenkte, standen nur unbezogene Farben vor seinem geistigen Auge und er entwickelte daher nur eine Übersicht der aus gesättigten Buntfarben und Weiß entstehenden Farben. Freilich wußte er, daß die Gesamtheit der Farben dreifaltig ist, und nicht zweifaltig, wie seine Übersicht. Der fehlenden dritten Dimension widmete er aber nur einen flüchtigen Hinweis, der zwar kurz, aber nicht gut war.
Darum hat weder er, noch irgendeiner seiner Nachfolger, welche sich der von ihm angegebenen Begriffe bedienten, eine Farbordnung schaffen können. Der Amerikanische Forscher O. Rood, Helmholtz's bester Schüler nach dieser Richtung, schrieb nach vieljähriger und oft fruchtbarer Arbeit: Tatsächlich sind weder unsere[371] Kenntnisse der Farbe noch unsere experimentellen Hilfsmittel zurzeit genügend vorgeschritten, um uns in den Stand zu setzen, einen Plan zu einer wirklich wissenschaftlichen Klassifikation der Farben auch nur vorzuschlagen. Und zwischen dem Vorschlag und der Ausführung würden noch viele mühselige Schritte liegen.
Goethe. Eine andere geschichtliche Aufklärung ergab sich für Goethes Stellung zu Newton und den Physikern seiner Zeit bezüglich der Farbenlehre. Er fühlte einen inneren Abscheu gegen deren Versuche und begann eines seiner Streitgedichte gegen Newton mit der Mahnung: Freunde, flieht die dunkle Kammer! Was er sachlich gegen die physikalischen Experimente einwandte, war nicht von Bedeutung, denn Goethe war alles andere als ein Physiker. Es handelte sich vielmehr um die unterbewußte Tatsache, daß er in der Farbenwelt der Physiker, die nur aus unbezogenen Farben bestand, die unverhältnismäßig viel reichere Farbenwelt, die er täglich mit seinen lichtdurstigen Augen aufnahm, nicht wiederfinden konnte. Daraus entstand ihm die unmittelbare Gewißheit, daß dort die Aufgaben nicht gelöst werden konnten, die seine Seele erfüllten, worin er durchaus Recht hatte. Aber da weder ihm noch seinen Gegnern die Begriffe der bezogenen und unbezogenen Farben bekannt waren, so mußte der Streit ungeschlichtet bleiben, bis er ein Jahrhundert später entschieden wurde.
Die entscheidende Rolle, welche hier vom Schwarz gespielt wird, war der Leitfaden, an welchem ich mich aus dem Helmholtzschen Irrgarten herausfand. Wenn durch die An- oder Abwesenheit von Schwarz zwei durch eine Dimension verschiedene Gruppen von Farben entstehen, von denen jede in sich geschlossen ist, so muß sicherlich Schwarz ein wahres Element der dreifaltigen Gruppe sein. War das so, so war ebenso sicher Weiß ein zweites Element. Und über das dritte war dann kein[372] Zweifel: es war die reine oder gesättigte Farbe, die ich, weil diese Namen schon mehrfach für etwas verschiedene Begriffe verbraucht waren, Vollfarbe nannte. Damit waren die drei Elemente der Farbe gegeben, durch deren unabhängige Abwandlung alle möglichen Farben entstehen mußten und in welche jede wirkliche Farbe muß aufgelöst werden können.
Als ich so weit war, fand ich beim Rückblick, daß nun alles wirklich in Ordnung war. Sind Vollfarbe, Weiß, Schwarz die Elemente, so liegt folgende Ordnung vor. Die unbunten Farben bestehen aus den Elementen Weiß und Schwarz, die unbezogenen aus Vollfarbe und Weiß, die bezogenen aus Vollfarbe, Weiß und Schwarz. Es bleibt noch die Möglichkeit einer zweifaltigen Farbengruppe aus Vollfarbe und Schwarz, für welche die Erfahrung keine Beispiele liefert, weil bisher ein Anteil Weiß bei allen Farben vorhanden ist. Aber es ist grundsätzlich wahrscheinlich, daß auch diese Gruppe verwirklicht werden wird. Ich gab es aber auf, nach ihr zu suchen, da es viel wichtiger war, vorher die Verhältnisse der bekannten Gruppen zu ermitteln.
Es soll hier alsbald eingeschaltet werden, daß dieselbe Zerlegung schon lange vorher von E. Hering gefunden worden war. Sein Weg war aber ganz verschieden von dem meinen. Er war psychologisch vorgegangen, ich dagegen ordnungswissenschaftlich. Nach dem allgemeinen Naturgesetz, daß man auf das Einfachste immer erst zuletzt kommt, war meine Ableitung viel einfacher und daher auch sicherer, als die von Hering, der sich auf die Empfindung berufen mußte, daß in jeder (bezogenen) Farbe eine gewisse Weißlichkeit und eine gewisse Schwärzlichkeit neben der Vollfarbe gesehen werden kann. Erwägt man, daß es nicht wenige Physiologen und Psychologen gegeben hat, welche im Grün als Bestandteile Blau und Gelb sehen zu können behauptet[373] haben, so erkennt man, warum Herings Zerlegung so wenig überzeugend gewirkt hatte.
Unter allen Umständen aber war die auf so verschiedenen Wegen erhaltene Übereinstimmung der Ergebnisse eine wertvolle Stütze für ihre Richtigkeit.
Die Zusammensetzung der Körperfarben. Die nächste Frage war, wie sich die so völlig einheitlich aussehenden Farbgemische, die wir in unserer Umgebung sehen, aus diesen Elementen zusammensetzen.
Im Falle der unbunten Farben war die Antwort bekannt. Jedes Grau besteht aus einem Bruchteil Weiß und einem Bruchteil Schwarz, und beide ergänzen sich zu eins. Bezeichnet man beide mit w und s, so gilt die Gleichung w + s = 1, wo w und s beide echte Brüche sind. Je größer w ist, um so heller ist das Grau, je kleiner, um so dunkler. Ideales Weiß enthält kein Schwarz, ist also durch w = 1 gekennzeichnet, ebenso ideales Schwarz durch s = 1, weil der weiße Anteil gleich Null ist.
Hier trat für mich alsbald die sorgenvolle Frage auf: woher kommt diese Eins? Die vielen hundert Gleichungen, welche in der Physik und Chemie durch meine Hände gegangen waren, hatten niemals eine solche absolute Zahl enthalten. Nur in einigen geometrischen Gleichungen war das vorgekommen, wie in der bekannten trigonometrischen Gleichung sin2x + cos2x = 1. Aber auch das ist selten. Unter welchen Bedingungen geschieht es?
Im Falle der Geometrie kann man die Sache begreifen. Eine Linie oder Fläche usw. kann bis ins Unbegrenzte ausgedehnt werden; hier tritt keine bestimmte Zahl auf. Aber ein Winkel kann nicht größer sein als vier Rechte; die Grenze der Winkel ist also endlich und deshalb die natürliche Einheit aller Winkel, die alsdann durch einen echten Bruch gemessen werden.
Dies erinnert aber alsbald an die Verhältnisse bei den grauen Farben. Bekanntlich kann man eine graue[374] Fläche dadurch herstellen, daß man einen weißen Grund mit kleinen schwarzen Punkten in gleichförmiger Verteilung bedeckt. Je größer der schwarze Anteil ist, um so dunkler ist das Grau. Aber diese Größe hat ein Ende, wenn die Punkte den ganzen Grund decken. Dieser ganze Grund ist also die Einheit, deren Bruchteile Weiß und Schwarz sind, die zusammen niemals mehr oder weniger ausmachen können, als eben diese Einheit.
Daher kam also die Eins in der Gleichung für Grau. Sie war ein Ausdruck für die ordnungswissenschaftliche Gesetzlichkeit, der die Bildung der Mischfarben aus ihren Elementen unterworfen ist. Weil man in eine Fläche nicht beliebig viel Weiß und Schwarz häufen kann, sondern nicht mehr oder weniger, daß beide zusammen die Fläche decken, kann man die Summe w + s nicht beliebig groß oder klein machen, denn sie bleibt von selbst sich immer gleich.
Man darf diese äußerst schlichten Überlegungen nicht für selbstverständlich halten. Ich weiß, was sie an Nachdenken gekostet haben, bis ich sie so schlicht hatte. Ihr eigentlicher Wert wird aber erst sichtbar, wenn man die Gedankenreihe weiter verfolgt, die durch sie aufgetan wird.
Geht man nämlich zu den dreifaltigen Buntfarben über, so erkennt man alsbald, daß die gleichen Überlegungen dazu führen, für diese eine Gleichung von der Gestalt v + w + s = 1 anzusetzen. Das heißt: jede Buntfarbe besteht aus drei Bruchteilen von Vollfarbe, Weiß und Schwarz, und die Summe dieser drei Brüche ist stets gleich Eins.
Man findet auf gleichem Wege die Veranschaulichung hierfür, wie bei den grauen Farben. Denn man braucht sich den weißen Grund nur mit Punkten von Vollfarbe und Schwarz nebeneinander besetzt zu denken, und hat dann vor Augen, warum die drei Anteile notwendig[375] echte Brüche sein müssen, und zusammen die ganze Fläche ergeben, welche die natürliche Einheit ist.
Während man sagen kann, daß die einfachere Gleichung der unbunten Farben, wenn auch vielleicht nicht klar ausgesprochen, doch vielfach stillschweigend vorausgesetzt worden ist, darf die Gleichung der Buntfarben als völlig neu betrachtet werden. Ihre Entdeckung lag für den ganz nahe, der sich über die Elemente der Farben klar geworden war. Hering aber, der diese Klarheit besaß, konnte von seinem psychologischen Standpunkt aus, ohne die Begriffe des reinen Weiß und der bezogenen Farben nicht nur keine Möglichkeit sehen, diese Bruchteile zu messen, sondern mußte sogar die Messung als unmöglich ansehen. In solchem Sinne schrieb er mir auch, als ich ihm brieflich mitteilte, daß ich eine solche Möglichkeit gefunden hatte und kennzeichnete so auf das bestimmteste den Punkt, wo die frühere, qualitative Farbenlehre in die neue, quantitative umgewandelt wurde. Es war kurz vor seinem Tode.
Die Entdeckung der Messung. Als ich so weit war, sah ich, daß die eigentlichen Schwierigkeiten der Aufgabe erst aufgedeckt, nicht aber überwunden waren. So schön und einfach die Gleichung v + w + s = 1 aussah, sie hatte so lange nur formale Bedeutung, bis die Mittel und Wege gefunden waren, für die Anteile ihre Zahlenwerte in jedem vorgelegten Falle ausfindig zu machen. Tatsächlich habe ich auf keinen Teil meiner Farbforschungen mehr Kopfbrechen verwendet, als auf diesen. Denn ich hatte mir vorgenommen, die hier nötige Entdeckung jedenfalls zu machen, da von ihr alle weiteren Fortschrittsmöglichkeiten abhingen.
Bisher hatte ich die mancherlei neuen Dinge, die ich zu entdecken so glücklich war, gefunden, wie man eine schöne Blume oder einen lieben Menschen findet: ich hatte die Augen offen gehalten und zugegriffen, wenn[376] etwas im Gesichtsfelde erschien, was der Mühe des Festhaltens wert sein mochte. Nur in einem einzigen Falle, bei meiner Faraday-Vorlesung (II, 370) hatte ich die Entdeckung, die ich mehr als Wunsch denn als Inhalt vor mir sah, nicht einfach gefunden, sondern durch bewußte Anstrengung erobert. Aber ich habe schon berichtet, daß der Energieaufwand hierbei viel größer war, als bei allen anderen Entdeckungen.
Nun war die Lage doch zum besseren verändert. Ich hatte mir eine weitgehende Klarheit über die Technik des Entdeckens und Erfindens und in der bewußten, schon von Leibniz empfohlenen Anwendung der Kombinatorik sowie der allgemeinen Ordnungslehre die dazu erforderlichen Hilfsmittel verschafft. Somit ging ich mit dem Vertrauen an die Arbeit, daß ich zum Ziel kommen würde. Denn unter diesen Gesichtspunkten kann man bei sich selbst eine Entdeckung bestellen, wie man beim Schneider ein Paar Hosen bestellt: man weiß, daß man sie bekommen wird, nur das ist zweifelhaft, wann man sie bekommt.
Um einen Wink zu gewinnen, wie die Aufgabe bei den Buntfarben gelöst werden konnte, vergegenwärtigte ich mir zunächst, wie sie bei den unbunten gelöst war. Hier handelt es sich um die beiden Größen Weiß und Schwarz, die zusammen Eins ausmachten. Man braucht also nur die eine von ihnen zu messen; die andere ist durch den Rest gegeben. Ich brauchte im Hasch nur in meßbarer Weise das Licht zu vermindern, das auf eine rein weiße Fläche fiel, bis diese ebenso aussah, wie die graue, und nachzusehen, welcher Bruchteil des ganzen Lichtes wirksam geblieben war, so kannte ich den Bruchteil Weiß im Grau. Schwarz war der Rest oder die Ergänzung zu Eins.
Gesetzt nun, ich könnte auf irgendeine ähnliche Weise den Weißanteil in der Buntfarbe messen: wäre[377] damit auch hier die Aufgabe gelöst? Offenbar nicht, denn außerdem war noch Schwarz und Buntfarbe vorhanden, zwischen denen noch alle möglichen Verhältnisse bestehen konnten. Denn in der Gleichung v + w + s = 1 können zwei Größen unabhängig voneinander verändert werden. Mit einer Messung ist also die Sache nicht erledigt; es müssen zwei sein.
Müssen es notwendig zwei sein? Lassen sich nicht Bedingungen finden, unter denen eine von den Größen keinen Einfluß hat? Kann mit anderen Worten nicht auf irgendeine Weise eines der Farbelemente unwirksam gemacht werden?
Es war ein erheblicher Fortschritt, als ich die Frage so weit gebracht hatte. Die Arbeit war um so schwieriger, als ich auf mich allein angewiesen war und niemand erreichen konnte, dem ich zumuten durfte, daß er sich in diese Fragen versenkte. Denn der Krieg wütete und nahm alle verfügbaren Energien in Anspruch.
Die gewonnene Fragestellung hatte aber das Wild, das ich erlegen wollte, auf ein mir schon einigermaßen bekanntes Gebiet gebracht, das der ausgezeichneten Fälle. Bei meinen Arbeiten zur Energetik war mir hier ein wichtiges Denkmittel begegnet, dessen ich mich mehrfach bedient hatte, um schwierige Fragen allgemeiner Natur so in die Enge zu bringen, daß ich sie beantworten konnte. Gelang es, auch für die Messung der Buntfarben den ausgezeichneten Fall zu finden und herzustellen, so war dort, mathematisch gesprochen, eine Veränderliche weniger vorhanden, und die Aufgabe war nicht schwieriger, als die Messung eines Grau.
Was ist ein ausgezeichneter Fall? Um diesen wichtigen Begriff kennen zu lernen, betrachten wir zunächst einige anschauliche Beispiele. Wir zeichnen uns eine nach unten durchgebogene Linie auf, etwa wie eine Kette, die locker an zwei Pfeilern hängt. Diese Linie enthält[378] unzählig viele Punkte, aber nur einen tiefsten. Deshalb nennen wir ihn den ausgezeichneten Punkt.
In einer Kreisfläche gibt es unzählige Punkte, von denen jeder die Eigenschaft hat, daß seine Abstände von den Punkten der Kreislinie verschieden groß sind. Nur einen Punkt gibt es, den Mittelpunkt, dessen Abstände alle gleich groß sind. Dieser ist daher ein ausgezeichneter Punkt.
Zwischen zwei Punkten kann man unzählige Linien ziehen. Unter ihnen gibt es nur eine, die Gerade, welche kürzer ist, als alle anderen. Sie ist daher eine ausgezeichnete Linie.
Solche Beispiele wird nun jeder leicht vermehren können. Man wird aber fragen: was kommt denn dabei heraus?
Es besteht das überaus wichtige und merkwürdige Gesetz, daß der ausgezeichnete Fall stets einfacher und leichter zu kennzeichnen ist, als alle anderen, benachbarten Fälle.
Bei der Kettenlinie besteht in jedem Punkt eine andere Neigung gegen die Wagerechte und um den Punkt zu kennzeichnen, muß der Neigungswinkel angegeben werden. Im ausgezeichneten Punkt besteht keine Neigung, denn die Berührungslinie, welche sie veranschaulicht, ist selbst wagerecht.
Um einen Punkt in der Kreisfläche zu kennzeichnen, müssen die zwei Abstände von zwei bestimmten Punkten der Kreislinie angegeben werden. Der Mittelpunkt braucht keine solche Kennzeichnung, denn er ist schon durch die Gleichabständigkeit festgelegt.
Um eine beliebige Linie, die zwischen zwei Endpunkten verläuft, zu kennzeichnen, braucht man unbegrenzt viele Angaben über alle ihre Teile. Die Gerade ist schon dadurch unverwechselbar gekennzeichnet, daß sie die kürzeste Linie ist.[379]
Es ist noch zu bemerken, daß es zuweilen mehrere ausgezeichnete Fälle gibt, wenn das Gebilde darnach beschaffen ist. So hat beispielsweise eine Ellipse zwei ausgezeichnete Punkte, die Brennpunkte.
Was hier an geometrischen Beispielen, welche die anschaulichsten sind, gezeigt worden ist, hat weit über die Geometrie hinaus Geltung. Die allgemeinsten Prinzipien der Mechanik und Physik sowie der höheren Wissenschaften lassen sich alle als besondere Ausgestaltung der Lehre vom ausgezeichneten Fall erkennen.
Für die Forschung ergibt sich daraus ein allgemeines Verfahren: Hat man ein verwickeltes Problem zu lösen, so suche man unter den zahllosen Einzelfällen, in denen es sich betätigt, den ausgezeichneten Fall auf, und man darf sicher sein, daß dort die Verwicklung geringer, das Problem also leichter lösbar sein wird.
Der ausgezeichnete Fall bei den Farben. Um diesen Gedanken wirksam zu machen, mußte ich nun den ausgezeichneten Fall (oder die ausgezeichneten Fälle) für die vorliegende Aufgabe ausfindig machen. Ich will nicht die mancherlei vergeblichen Bemühungen beschreiben, die mich quälten; ich habe sie glücklicherweise vergessen. Die erfolgreichen Gedanken waren folgende.
Wodurch ist die Buntfarbe von der grauen verschieden? Durch die Anwesenheit der bunten Vollfarbe. Kann ich diese auf irgendeine Weise unwirksam machen, so wird sie mich bei der Messung nicht mehr behindern.
Kann ich nun der bunten Umwelt ihre Buntheit nehmen? Natürlich nicht unmittelbar, sondern nur in ihrem Aussehen, für mein Auge. Ja, wenn ich sie durch ein rotes oder blaues oder sonst tief gefärbtes Glas betrachte. Durch ein blaues Glas sieht die ganze Welt blau aus, aber nicht gleichförmig, sondern mit Schatten und Licht, wie ein unbuntes Bild. Wenn ich also irgendein buntes Papier durch das blaue Glas an sehe, so wird[380] es ein bestimmtes Blau zeigen, welches ebenso hell oder dunkel aussieht, wie ein passend gewähltes Grau; ich bin also in ganz ähnlichen Verhältnissen, wie bei der Messung eines grauen Papiers mittels der Grauleiter. Wie das aber zu deuten ist, weiß ich noch nicht.
Hier kommt nun der Satz vom ausgezeichneten Fall zu Hilfe, da in ihm die Verhältnisse einfacher werden. Gegeben sei ein rotes Papier; wo ist hier der ausgezeichnete Fall zu finden? Offenbar, wenn das bunte Glas oder Lichtfilter auch rot ist. Und noch einen ausgezeichneten Fall gibt es: jede bunte Farbe hat ihre Gegenfarbe (Komplementärfarbe), die ihr polar gegenübersteht. Also auch ein seegrünes Lichtfilter wird einen ausgezeichneten Fall ergeben, denn Seegrün ist die Gegenfarbe von Rot.
Wir betrachten zuerst den zweiten Fall; er hat sich als der einfachere herausgestellt. Das seegrüne Filter hat die Eigenschaft, daß es alles rote Licht verschluckt und nur grünes durchläßt. Wäre mein rotes Papier rein rot, so würde es hinter dem seegrünen Filter vollkommen schwarz aussehen. Solche Papiere gibt es nicht; neben der roten Vollfarbe ist immer noch Schwarz und Weiß vorhanden und solches Papier ist hinter dem Filter nicht rein schwarz, sondern heller.
Wovon? Das rote Licht geht nicht durch; der schwarze Anteil gibt kein Licht. Wohl aber der weiße Anteil. Weißes Licht enthält alle Farben vollständig, also auch Seegrün. Soviel Weiß im roten Papier vorhanden ist, soviel Seegrün geht durch das Filter. Dasselbe gilt für den weißen Anteil im Grau der Grauleiter. Sehen beide gleich aus, so enthalten beide also gleich viel Weiß. Da man den Weißgehalt der Grauleiterstufen kennt, so kennt man auch den Weißgehalt des roten Papiers.
Ich war unbeschreiblich froh, als ich so weit gekommen war. Denn dies war eine Entdeckung, die ich[381] nicht dem Glück verdankte, sondern der methodischen Einkreisung meiner Aufgabe durch angemessene Gedanken, bis die Beute fest in meiner Hand war.
Und es handelte sich hierbei um mehr als den besonderen Fall, so wichtig er auch war. Ich hatte mir selbst bewiesen, daß man wirklich das Entdecken organisieren kann. Das bedeutete einen großen Sieg meines führenden Grundgedankens: daß der Wissenschaft alles zugänglich ist, und daß man daher das Entdecken ebenso lehren und lernen kann wie das Radeln.
Ob ich es damit für andere bewiesen habe, muß ich allerdings bezweifeln.
Denn ich höre die heute so zahlreichen Mystiker und Anhänger der Intuition beim schöpferischen Menschen heftig dagegen protestieren. Sie sagen: Ostwald irrt. Wir geben zu, daß er die Entdeckung gemacht hat, und daß sie bedeutend ist. Aber er irrt, wenn er meint, daß er durch seine sogenannte methodische Arbeit dazu gelangt ist (die wir nicht kennen und daher verachten). Der Kerl ist nämlich einfach ein Genie und macht seine Entdeckungen durch Intuition, wie das einem Genie zukommt. Er bildet sich nur nachträglich ein, daß er das mit seinem dürftigen Verstande selbst gemacht hat, was ein Gnadengeschenk des Weltgeistes ist.
Ich muß bekennen, daß ich dagegen wehrlos bin. Nur kann ich auf keine Weise herausbringen, woher sie das so genau wissen. Denn selbst machen sie keine wertvollen Entdeckungen, trotz ihrer intimen Beziehungen zum Weltgeist.
Wir haben noch den zweiten (eigentlich ersten) ausgezeichneten Fall zu untersuchen, nämlich daß wir das rote Papier durch das rote Filter betrachten. Nun geht alles Rot vom Papier durch, auch aus dem Weiß, und wenn die Farbe des Papiers nur Rot und Weiß enthielte, so würde es ebenso hell aussehen, wie ein weißes Papier.[382] Der schwarze Anteil aber, wenn er vorhanden ist, wirft kein Licht zurück und läßt das Papier entsprechend dunkler erscheinen. Finde ich also ein Graupapier, das hinter dem roten Filter ebenso hell aussieht, wie das rote, so enthalten beide gleich viel Schwarz.
Damit sind die Zahlenwerte von Weiß und Schwarz bestimmt. Zieht man sie von Eins ab, so erfährt man, wieviel Vollfarbe vorhanden ist und in der Gleichung v + w + s = 1 ist jeder einzelne Wert bekannt. Die Aufgabe einer Messung der Farbelemente ist gelöst. Sie war durch die früheren Forscher nicht einmal gestellt, geschweige denn gelöst worden.
Nachdem der grundlegende Gedanke gewonnen war, ließ sich seine Übersetzung in das Gebiet der praktischen Anwendung verhältnismäßig leicht ausführen. Zwar hatte ich früher kaum je Gelegenheit gehabt, optische Geräte zu entwerfen. Aber was hier nötig war, ließ sich mit so einfachen Hilfsmitteln erledigen, daß ich mir den Farbmesser (das Chrometer) alsbald selbst erbauen konnte und ihn jahrelang täglich benutzt habe, auch als mir hübschere, vom Mechaniker erbaute Ausführungen längst zu Gebote standen.
Das ganz unbekannte Neuland, welches mir derart zugänglich geworden war, gab reichliche Arbeit für mehrere Jahre, bis die Hauptpunkte festgestellt und ihre gegenseitigen Beziehungen ermittelt waren. Dabei wurde beständig Gebrauch von der Gleichung v + w + s = 1 gemacht, für deren Richtigkeit zahlreiche Bestätigungen gefunden wurden.
Das farbtongleiche Dreieck. Es entstand nun die Frage, wie die unabsehbare Menge aller Farben zu ordnen sei, die aus Vollfarbe, Weiß und Schwarz entstehen können, wenn diese in allen denkbaren Verhältnissen gemäß der Gleichung v + w + s = 1 gemischt werden. Mit Rücksicht auf die begrenzte Unterscheidungsfähigkeit[383] des Auges, die »Schwelle« kann man die Anzahl der unterscheidbaren Farben auf eine bis zehn Millionen, vielleicht noch höher schätzen. Diese ungeheuere Menge galt es so zu ordnen, daß jede einzelne Farbe aus den Millionen ihren ganz bestimmten, unmittelbar auffindbaren Platz erhielt. Wenn die seinerzeit erwähnte Ordnungswissenschaft oder Mathetik etwas wert war, so konnte sie das hier erweisen.
Ein wesentlicher Teil dieser Arbeit war schon vor mehr als hundert Jahren durch Deutsche Forscher geleistet worden; Tobias Mayer, Johann Lambert, Philipp Runge sind hier zu nennen. Das Hauptergebnis war, daß die Gesamtheit aller Farben sich nicht in einer Linie oder Fläche abbilden läßt, sondern nur in einem räumlichen Gebilde, einer dreiseitigen Pyramide (Lambert) oder Kugel (Runge). Ihre Ergebnisse wurden in den Hintergrund gedrängt durch das sehr anspruchsvoll auftretende System des Franzosen Chevreul, das von mehreren Seiten anzuwenden versucht wurde. Doch endeten alle diese Ansätze in Mißerfolg, weil das System in sich fehlerhaft ist. Da in allen Fällen die Einteilung der Farben in Ermangelung eines objektiven Verfahrens der Messung auf bloßer Schätzung beruhen mußte, so konnte sich keiner dieser Versuche durchsetzen, wenn auch gewisse grundlegende Ordnungen sich dabei herausstellten.
Von den neueren Forschern ist der Lösung der Aufgabe am nächsten gekommen Ewald Hering, der als Nachfolger Karl Ludwigs (II, 82) einige Jahre mein Kollege an der Leipziger Universität war. Ihm verdanken wir den Begriff des farbtongleichen Dreiecks, nämlich der Gesamtheit aller Farben, die von einer gegebenen Vollfarbe dadurch abgeleitet werden können, daß man sie in allen denkbaren Verhältnissen mit Weiß und Schwarz und beiden vermischt. Er erkannte[384] ganz richtig, daß jeder Körperfarbe neben ihrem bunten Farbton noch eine gewisse Weißlichkeit und eine gewisse Schwärzlichkeit zukommt, die beide stärker oder schwächer vorhanden sein können und so das Aussehen der Farbe bestimmen. Ferner zeigte er, daß man die hier vorhandenen Möglichkeiten erschöpfen kann, wenn man alle derartigen Abkömmlinge einer gegebenen Körperfarbe in einem Dreieck anordnet, in dessen Ecken sich Vollfarbe, Weiß und Schwarz befinden, zwischen denen nach allen Richtungen im Dreieck stetige Übergänge bestehen.
Dies war alles ganz richtig. Leider stellte aber Hering die Möglichkeit in Abrede, in diese Verhältnisse messend einzudringen und verfehlte auf solche Weise die Vollendung seines guten Gedankens. (III, 373.)
Hier konnte ich seine Arbeit aufnehmen und fortsetzen, nachdem ich die Messung der Farben ermöglicht hatte. Stellt die Linie WS die Gesamtheit der unbunten Farben von Weiß (W) über Grau bis Schwarz (S) dar, so muß eine Vollfarbe, da sie bunt ist, notwendig außerhalb dieser Linie untergebracht werden. Wir setzen sie nach V. Dann liegen auf der Linie VW alle Mischungen aus der Vollfarbe und Weiß, auf VS alle aus der Vollfarbe mit Schwarz. Im Inneren des Dreiecks liegen alle Mischungen, welche neben der Vollfarbe gleichzeitig Weiß und Schwarz enthalten; sie heißen trübe Farben. Längs der Linie VG, welche von der Vollfarbe zu irgendeinem Grau G geht, liegen alle Mischungen der Vollfarbe mit diesem Grau. Da solche Linien zu jedem Punkt der unbunten Reihe WS gezogen werden können, sind die Mischungen mit jedem möglichen Grau vorhanden. Das Dreieck umfaßt also in der Tat alle denkbaren Abkömmlinge der[385] gewählten Vollfarbe. Da durch die Größe der Abstände die Mischungsverhältnisse zahlenmäßig dargestellt werden, so stellt jeder Punkt des Dreiecks ein ganz bestimmtes Gemisch dar; wir haben hier also eine vollständige zahlenmäßige Abbildung aller Abkömmlinge eines gegebenen Farbtons.
Für mich entstand nun die Aufgabe, solche farbtongleiche Dreiecke für die verschiedenen Farbtöne herzustellen, um eine Anschauung davon zu gewinnen, wie solche Dreiecke überhaupt aussehen. Denn bisher hatte noch keines das Licht des Tages erblickt. Ich erschrak zunächst vor der Größe der Arbeit. Da ich diese aber zunächst auf einige Hauptpunkte beschränken und sie nach Bedarf mehr und mehr in die Einzelheiten führen konnte, so lag die Ausführung doch im Bereich der Möglichkeiten, so sehr diese damals durch den Krieg eingeschränkt waren. Eine unbedingte Voraussetzung war freilich eine gute Kenntnis der Farbstoffe und der Arten ihrer Anwendung. Sie war im vorliegenden Falle erfüllt, was sonst bei den Farbforschern nicht der Fall zu sein pflegt, und dies erklärt, warum dieses Mal ein Erfolg erreicht wurde.
Der Farbtonkreis. Ehe ich indessen an diese Arbeit gehen konnte, war noch eine Frage klarzustellen, welche die bisherige Wissenschaft unbeantwortet gelassen hatte, nämlich die nach der richtigen Anordnung oder Einteilung des Farbtonkreises. Farbton ist der allgemeine Name für jene Eigenschaft der Buntfarben, welche man in den Einzelfällen Gelb, Rot, Blau, Grün nennt. Wir haben eben gesehen, daß es zahllose Farben gleichen Farbtons gibt, nämlich alle, die in demselben Dreieck untergebracht sind. Man muß also die Begriffe Farbe und Farbton genau unterscheiden. Farbe ist die Einzelerscheinung von bestimmtem Farbton, Weiß- und Schwarzgehalt; Farbton[386] ist der allgemeinere und unbestimmtere Begriff, der von dem unbunten Anteil unabhängig ist.
Von den Farbtönen war längst bekannt, daß sie sich zu einer in sich zurücklaufenden Reihe ordnen lassen, die man am einfachsten in Gestalt eines Kreises darstellt, die der Farbenkreis, genauer der Farbtonkreis heißt. Geht man also von einem bestimmten Farbton aus, so sind die im Kreise benachbarten diesem ähnlich: der Farbtonkreis ist stetig. Je weiter man kommt, um so unähnlicher wird der Farbton dem Ausgangston. Das geht aber nicht unbegrenzt weiter, denn nachdem ein unähnlichster Punkt, der Gegenfarbton erreicht ist, werden die folgenden Farben wieder ähnlicher, bis beim Ausgangspunkt der stetige Anschluß erreicht ist. Es gibt ein Mittel, solche Gegenfarbenpaare genau zu bestimmen: sie ergeben beim Mischen neutrales Grau. Man kann fordern, daß Gegen-Farbtöne sich im Kreise gegenüber liegen sollen. Das ist der erste Schritt zur Festlegung der Farbtöne im Kreise; er ist aber noch nicht genügend.
Im Farbtonkreise sind zwar die Farbtöne nach einer stetigen Folge aufgereiht, über die kein Zweifel besteht. Aber nur die Reihenfolge ist zweifellos, ähnlich wie die von Perlen, die locker auf einem Faden gereiht sind; Ebenso, wie die Perlen sich hier dicht, dort locker folgen können, so können im Farbtonkreise die Farbtöne enger oder weiter angeordnet werden. Ich fand in der vorhandenen Wissenschaft keinen Grundsatz vor, der hier eine Entscheidung fällte. Wiederum konnte ich das Verfahren des ausgezeichneten Falles anwenden und unter den möglichen Anordnungen die mit der Eigenschaft der Einmaligkeit behaftete aufsuchen. Ich legte sie meinem Farbtonkreise zugrunde und kann mitteilen, daß er sich inzwischen zunehmend als der beste durchgesetzt hat.[387]
Bei diesen Arbeiten stieß ich auf einen schweren Block, der lange hart auf meinem Denkgewissen lastete. Bekanntlich zeigt das Spektrum, die Anordnung der Lichter nach ihren Wellenlängen, dieselbe Reihenfolge, wie der Farbtonkreis, nur mit einer Lücke im Purpur, das im Spektrum nicht vorkommt. Das rote Licht hat die längsten Wellen, dann kommt Kreß (Orange), Gelb, Laubgrün, Seegrün, Eisblau, Ublau (Ultramarinblau), Veil (Violett); dieses hat die kürzesten. Nach den Wellenlängen beurteilt, müßten also Rot und Veil die größte Verschiedenheit im Aussehen haben, weil bei ihnen der größte Unterschied der Wellen besteht. Das ist aber keineswegs der Fall, vielmehr stehen sich Rot und Veil im Aussehen sehr nahe, viel näher als etwa Rot und Grün. Während also die Empfindungen der Farbtöne sich zu einem Kreise schließen, verlaufen die Wellenlängen, die mit den Farbtönen eindeutig verknüpft sind, einsinnig von einem größten bis zu einem kleinsten Wert. Wären die Wellenlängen unmittelbar maßgebend für die Empfindung, so müßten die Farbtöne eine Ordnung zeigen, wie die unbunten Farben: eine stetige Reihe, mit dem größten Unterschied an beiden Endpunkten.
Daß über diesen Block noch niemand gestolpert war, kann ich nur dem Umstande zuschreiben, daß solche einfache ordnungswissenschaftliche Betrachtungen selbst Fachleuten, die sonst sehr gute Einzelkenntnisse besitzen, noch ganz ungeläufig sind, so daß sie die Sache nicht einmal verstehen, wenn man sie ihnen begreiflich zu machen versucht. Das ist die Folge der Vernachlässigung dieser Grundlage aller anderen Wissenschaften.
Das Farbenhalb. Einen anderen Block hatte zwar schon Schopenhauer gesehen und gekennzeichnet; da aber niemand ihn zu beseitigen wußte, hat man ihn ein Jahrhundert lang liegen gelassen und umgangen. Er liegt in den folgenden Tatsachen.[388]
Reines, gesättigtes Gelb, z.B. helles Kadmiumgelb, ist fast so hell wie Weiß. Im Spektrum macht Gelb etwa ein Zwanzigstel aus. Wenn die Körperfarben dadurch zustande kämen, wie man in allen Lehrbüchern las, daß nur die betreffenden Lichter zurückgeworfen, alle anderen verschluckt werden, so müßten gelbe Farbstoffe schwarz aussehen, denn schon bei 1/10 Rückwurf beginnt das Schwarz. Ähnlich, wenn auch nicht so auffallend ist es mit den anderen Farben.
Um selbst zu sehen, wie die Sachen liegen, sah ich mir eine rein gelbe Lösung mit dem Spektroskop an; Nebenlicht war ausgeschlossen. Ich sah nicht etwa den gelben Teil des Spektrums allein, wie ich erwartete, sondern sah den ganzen langwelligen Teil, Rot, Kreß, Gelb und Grün so hell, wie wenn gar nichts vor dem Spektroskop wäre. Blau und Veil war verschwunden; die Grenze ging durch das Seegrün. Ich wechselte den Stoff, denn es gibt recht viele gelbe Stoffe. Immer sah ich dasselbe Bild: der größere und hellste Teil des Spektrums ging ungeschwächt durch und die Grenze blieb dieselbe bei reinem Gelb; bei rötlichem verschob sie sich etwas nach den längeren Wellen.
Hunderte, vielleicht Tausende von Physikern, Physiologen, Psychologen, Farbchemikern usw. hatten dies vor mir gesehen und mancher hat sich auch darüber gewundert. Aber keiner hatte sich entschlossen, zuzugeben, daß alle diese roten, kressen, gelben und grünen Lichter notwendig sind, um das Gelb der Körperfarben, das bezogene (III, 369) Gelb zu erzeugen. Solche Gewalt haben die in der Schule aufgenommenen Ansichten über den Erwachsenen, selbst wenn er sonst an wissenschaftliches Denken gewöhnt ist, daß er nicht sehen will, was er vor Augen hat. Die Wichtigkeit der Aufgaben, denen ich mich bei der Schulreformbewegung hingegeben hatte, trat mir hier nochmals eindrucksvoll in das Bewußtsein.[389]
Ich war bei diesen Forschungen entschlossen, keinen solchen Block liegen zu lassen. So sah ich mich genötigt, den Gedanken nicht nur zuzulassen, sondern in den Mittelpunkt der Begriffsbildung zu stellen, daß zur Entstehung der bezogenen Farben auch im reinsten Zustande ein ganzer Fächer von Spektralfarben gehört. In meinen Schriften über Farbenlehre kann man nachlesen, wie die hier vorhandenen Tatsachen zu der Lehre vom Farbenhalb organisiert wurden, welche nicht nur die beiden beschriebenen Blöcke der Widersprüche (auch den wegen der Purpurfarben) beseitigt, sondern außerdem nach vielen Seiten neue Aufklärung gibt. Nur eine allgemeine Betrachtung soll hier mitgeteilt werden.
Entwicklungsgeschichtliches. Goethe schreibt in der Einleitung zu seiner Farbenlehre: »Das Auge hat sein Dasein dem Licht zu verdanken. Aus gleichgültigen tierischen Hilfsorganen ruft sich das Licht ein Organ hervor.« Die spätere Entwicklungsgeschichte hat diese Vorausnahme voll bestätigt. Zum Verständnis des Sehens ist es also notwendig, sich die Entwicklung des Auges gegenwärtig zu halten.
Niemals hat ein Lebewesen in der Natur Gelegenheit, Licht zu sehen, das nur aus Wellen gleicher Länge besteht; homogenes Licht nennt es die Physik. Immer und überall wirken auf das Auge nur Gemische benachbarter Wellenlängen über breite Gebiete des Spektrums. Das primitive Auge ist für Unterschiede der Wellen überhaupt nicht empfänglich; es sieht nur unbunt. Bei höherer Entwicklung werden grobe Unterscheidungen zu machen begonnen, aber auch für das feinst entwickelte Auge des Farbenkenners gibt es zahllose verschiedene Lichtgemische, die er nicht unterscheiden kann. Es bestand während der ganzen Entwicklungsreihe vom primitiven Pigmentfleck bis zum Künstlerauge niemals die Möglichkeit der Anpassung an homogene Lichter, weil solche[390] nie auf das Auge wirkten. Die dem Physiker nahe liegende Annahme, die homogenen Lichter, die ihm das Prisma nebeneinander legt, seien nicht nur die physikalischen, sondern auch die psychophysischen Elemente des Sehens, die von den früheren Farbenforschern als selbstverständlich, d.h. ohne Prüfung gemacht und benutzt wurde, ist ein schwerer Irrtum. Zu einer so weitgehenden Zerlegung ist das Auge bei weitem nicht fähig. Möglicherweise wird eine solche Fähigkeit in fernster Zukunft als Zielpunkt der Entwicklung des Auges erreicht werden. Zurzeit aber sind wir noch um Siriusweiten davon entfernt. Die Lehre vom Farbenhalb stellt nun die Stufe der Entwicklung fest, auf welcher wir uns seit geschichtlicher Zeit befinden. Auch ist kein deutliches Zeichen dafür vorhanden, daß wir uns darüber hinaus zu entwickeln angefangen haben. Eine heutige Farbenlehre hat also diesen Zustand genau zu definieren und seine Verhältnisse zu untersuchen. Das ist es, was ich mir zur Aufgabe gestellt hatte. Es gelang so weit, daß wir uns im Farbtonkreise zu Hause fühlen können.
Als ich so weit gekommen war, stand ich vor der Aufgabe, von jeder beliebigen Farbe, ob klar oder trübe, den Farbton festzustellen. Hierfür wurde wieder ein recht einfaches Gerät erfunden, der Polarisations-Farbenmischer, genannt Pomi. Er gestattet, wenn ein hinreichend eingeteilter Farbtonkreis gegeben ist, für jede vorgelegte Farbe den Punkt zu bestimmen, an den ihr Farbton gehört.
Die Herstellung dieses geteilten Farbtonkreises war wieder eine lange und schwierige Arbeit, für welche zahllose Einzelheiten als Vorarbeit erst noch erforscht werden mußten. Wegen der Zehnerordnung wählte ich eine Teilung des Kreises in hundert Farbtongrade, die schon nahe an der Grenze der Unterscheidbarkeit liegen. Als er fertig war, hatte ich die Aufgabe gelöst, jede vorgelegte Farbe[391] erschöpfend nach Farbton, Weißgehalt und Schwarzgehalt zu kennzeichnen. Die gesamte Farbenwelt war der Herrschaft von Maß und Zahl unterworfen.
Bedeutung der Farbenmessung. Kultur ist das geistige Kapital der Menschheit. Damit es angesammelt werden kann, muß die Möglichkeit bestehen, was der einzelne erarbeitet hat, über Raum und Zeit den Nachfahren mitzuteilen und zu erhalten. Hierzu dienen Sprache und Schrift; ohne sie gibt es keine Kultur.
Eine Sprache und Schrift für die Farbe gab es bisher nicht. Daher gibt es auch keine Kultur der Farbe. Der Berliner Psychologe v. Alesch hat vieljährige Untersuchungen über diese Frage angestellt und ist erfahrungsmäßig zu dem gleichen Ergebnis gekommen. Obwohl ich mein ganzes Leben lang beständig mit Farben umgegangen war und ihnen die lebendigste Teilnahme gewidmet hatte, war ich bis vor wenigen Jahren irgendeinem Bilde, einem Ornament, einem garnierten Damenhut gegenüber nicht in der Lage zu sagen: das ist gut in der Farbe, das übel. Denn wenn ich mich selbst befragte, erhielt ich keine Antwort. In den eben erwähnten Untersuchungen hat v. Alesch das gleiche Farbengebilde denselben Menschen zu verschiedenen Zeiten vorgelegt und diese haben sehr verschiedene, nicht selten vollkommen entgegengesetzte Urteile darüber gefällt. Alles, was man bei wohlwollendster Ausdehnung des Begriffes Farbenkultur nennen kann, beschränkt sich auf die Leistungen einzelner Personen. Diese vermögen aber ihr Können nicht auf andere zu übertragen. Das ist nicht der Zustand der Kultur, sondern der, wie er vor Beginn der Kultur bestand.
Warum kann der einzelne sein Farbkönnen nicht weitergeben? Weil er keine Worte dafür hat. Man versuche, ein farbschönes Muster einfachster Art so zu beschreiben, daß ein anderer nach der Beschreibung, ohne das[392] Muster zu sehen, eine ebenso farbschöne Nachbildung erzeugt. Es ist unmöglich. Und wenn der Schöpfer des Werkes selbst sein Muster wiederholt, ohne es vor Augen zu haben, wird er vielleicht ein ebenso schönes hervorbringen. Aber es werden nicht dieselben Farben sein, weil er seine Farben nicht benennen und sie daher nicht auswendig lernen kann. Deshalb müssen wir einen so übertriebenen Wert auf die Originalwerke unserer Meister legen, weil sie Einzelwesen sind, die vollkommen verschwinden, wenn sie irgendwie zerstört werden, was an Ölgemälden, wie sie heute gemalt werden, unvermeidlich beim bloßen Aufbewahren erfolgt. Was Tonkünstler und Dichter vor Jahrhunderten geschaffen hatten, liegt unzerstörbar in Noten und Büchern gesichert und kann jederzeit zu neuem Leben erweckt werden. Bei Bildern ist es unmöglich, was ihre Farbe anlangt. Und warum? Weil man Farben nicht aufschreiben kann. Oder genauer gesagt, bisher nicht aufschreiben konnte.
Denn jetzt kann man es. Man kann den Farbton und den Gehalt an Weiß und Schwarz messen und gibt man die gefundenen drei Zahlen an, so ist die Farbe genau und für alle Zukunft bezeichnet. Sie kann gesprochen, geschrieben, telegraphiert, durch Rundfunk verbreitet werden. Jenes schöne Muster, von welchem oben die Rede war, kann gemessen und danach jederzeit mit vollkommen gleicher Wirkung wiederhergestellt werden, wenn man in eine Zeichnung die »Kennzahlen« der zugehörigen Farben einschreibt. Diese stellen dasselbe dar, was die Noten bei einem Tonwerke, die Buchstaben bei einem Dichtwerke sind.
Man sollte meinen, daß insbesondere die Vertreter der Kunstgeschichte mit Begierde dieses Mittel ergreifen würden, um ihrer Wissenschaft endlich durch Maß und Zahl Exaktheit und Klarheit zu geben. Als ich aber[393] im Herbst 1919 in Stuttgart auf einer Werkbundtagung öffentlich Nachricht von diesen meinen Arbeiten gegeben hatte, verfaßten sie eine Schrift, in welcher meine Tätigkeit als im höchsten Grade schädlich beschrieben wurde, sammelten Unterschriften dazu und versandten das Schriftstück an alle Deutschen Unterrichtsministerien mit dem dringenden Ersuchen, insbesondere das Eindringen der messenden Farbenlehre in die Schulen mit allen Mitteln zu verhindern.
Neue Arbeit. Nachdem alles dies erreicht war, sah es einen Augenblick lang so aus, als könnte die Arbeit abgeschlossen werden. Nicht als wäre der Gegenstand erschöpft gewesen – ich habe keineswegs über alle Fragen berichtet, die im Zusammenhange mit jenen Forschungen beantwortet wurden – denn kein wissenschaftliches Problem kann jemals erschöpft werden. Sondern weil der erreichte Standpunkt bereits nach der praktischen wie theoretischen Seite Anderen so viel neue Forschungsarbeit ermöglichte, daß für lange Zeit vorgesorgt war.
Aber es lag noch ein neues Feld von größter praktischer Wichtigkeit vor, das jedenfalls Beackerung verlangte. Im unbunten Gebiet war nicht nur Ordnung und Messung durchgeführt worden, sondern auch Normung. Es war aus der Unendlichkeit der verschiedenen Grauabstufungen eine bestimmte Anzahl gleichabständiger Farben ausgewählt worden, welche als Vertreter ihrer näheren Nachbarn dienen können, so daß man mit 10, oder mit 20 solcher Graunormen so gut wie alles ausrichten kann, was man bisher mit unbestimmt vielen machte. Zudem waren für diese Normen Zeichen in Gestalt von Buchstaben festgesetzt worden, welche ihre Handhabung überaus leicht machen. Wird angegeben, daß ein Damenkleid in Grau g gehalten sein soll, mit Ausputz in e und i, so ist damit eine ganz eindeutige Kennzeichnung der Farbe dieser wichtigen Sache gegeben.[394]
Ebenso, wie die grauen Farben geordnet und genormt waren, wollten die bunten es werden. Da aber die grauen Farben einfaltig sind, die bunten dreifaltig, so war die Aufgabe hier sehr viel verwickelter. Und bei der Lösung war ich nicht mehr ganz frei. Denn die grauen Normen lagen bereits fest und nach dem oben ausgesprochenen Grundsatz mußten die neuen Normen mit den älteren im Einklang stehen, wo sie sich irgendwie berührten.
Das Fechnersche Gesetz bei den Buntfarben. Zunächst fing ich mit dem Einfachsten an, indem ich eine möglichst reine Vollfarbe z.B. Zinnober mit Weiß stufenweise aufhellte. Anfangs hatte ich das Weiß eine gleichabständige (arithmetische) Reihe bilden lassen, 1/10, 2/10, 3/10 usw. Das Ergebnis war ganz ähnlich wie beim Grau (III, 366); die Abstände waren am weißen Ende zu klein, am bunten zu groß. Das Rot des Zinnobers verhielt sich also gegen Weiß ganz ähnlich als wäre es Schwarz. Die Folgerung war gegeben: auch für diese Mischung gilt das Fechnersche Gesetz und wir müssen das Weiß nach einer geometrischen Reihe abstufen.
Aber nach welcher? Die Antwort war schon bereit: es mußten die gleichen Weißanteile genommen werden, wie in der Graureihe cegilnp. (Da a reines Weiß ist, kam es hier nicht in Frage.) Denn was einmal genormt ist, muß so bleiben. Hier gilt es für den Weißanteil.
Beim Schwarz ergaben sich ganz ähnliche Verhältnisse. Auch hier gilt das Fechnersche Gesetz, aber nun übernimmt die Vollfarbe die Rolle des Weiß gegenüber dem Schwarz.
Wie soll nun das Schwarz abgestuft werden? Offenbar wie das Schwarz in der Graureihe acegilnp. Der Versuch zeigt in einem wie dem anderen Falle, daß die so gebildeten Leitern für die Empfindung gleiche Abstände aufweisen.
[395] Das farbtongleiche Dreieck. Damit sind die Mischungen mit Weiß oder Schwarz allein genormt. Es fehlen aber noch die Mischungen, welche gleichzeitig Weiß und Schwarz enthalten. Die ersten Mischungen nennen wir hellklar und dunkelklar; die mit Grau trübe. Es steht also noch die Normung der trüben Farben aus.
Hier hatte Hering schon vorgearbeitet, indem er nachgewiesen hatte, daß alle Abkömmlinge, die aus einer Vollfarbe durch Zusatz von Weiß und Schwarz entstehen, sich in einem Dreieck unterbringen lassen, in dessen Ecken reine Vollfarbe v, Weiß w und Schwarz s liegen (III 384). Dann liegen in der Seite vw die hellklaren, in vs die dunkelklaren Farben, während ws die altbekannte Graureihe enthält. Im Inneren aber liegen alle trüben Farben, welche gleichzeitig Weiß, Schwarz und Vollfarbe enthalten.
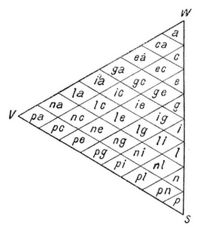
Untersucht man die Geometrie dieser Anordnung näher, so findet man allerlei höchst lehrreiche Beziehungen, welche die Beschäftigung damit zu einem wahren Vergnügen machen. Hier soll nur über das Endergebnis bezüglich der Normung berichtet werden. Man kann es aus dem beistehenden Bild ablesen.
Jedes Feld bedeutet eine Normfarbe. Von den beiden Buchstaben darin bedeutet der erste den Weißgehalt, der zweite den Schwarzgehalt, wie er in dem gleichnamigen Grau vorhanden ist. Wie man sieht, laufen von links nach rechts schräg nach unten Reihen mit gleichem ersten Buchstaben, d.h. gleichem Weißgehalt, schräg[396] nach oben Reihen mit gleichem zweiten Buchstaben oder Schwarzgehalt: die Weißgleichen und die Schwarzgleichen. Senkrecht laufen die Schattenreihen.
Eine etwas eingehendere Untersuchung, und noch besser die Anschauung eines ausgeführten Dreiecks zeigt, daß sich um v die reinfarbigen, um w die weißlichen und um s die schwärzlichen Abkömmlinge des Farbtons sammeln; überall grenzen die ähnlichsten Farben aneinander. Wer als mit Farben Vertrauter, also als Maler oder Färber zum ersten Male ein solches Dreieck sieht, erlebt eine beglückende Offenbarung. Ich habe das nicht nur an mir erprobt, sondern an unzähligen Anderen. Denn man fühlt zum ersten Male den strengen, inneren Zusammenhang der ganzen Farbenwelt und erkennt grundlegende Beziehungen, die man geahnt aber nicht gewußt hat. Was sich z.B. als Abkömmling von Gelb auswies, hat seinerzeit in mir einen Sturm freudiger Erregung ausgelöst, wie wenn der Nebel plötzlich von einer Fernsicht fortgeweht wird, die sich alsdann in Glanz und Schönheit entfaltet.
Das Dreieck enthält nämlich alle möglichen Verbindungen der genormten Weiß- und Schwarzmengen mit der Vollfarbe. Diese bilden die Normen aller Buntfarben, welche von derselben Vollfarbe durch Zumischung von Weiß und Schwarz abgeleitet werden können, also die vollständige Normentafel dieser Vollfarbe bis p. Alle darin enthaltenen Farben haben den gleichen Farbton, das Dreieck heißt deshalb auch das farbtongleiche Dreieck.
Meinem denkerischen Gewissen war es eine unbeschreibliche Beruhigung, als ich dieses Dreieck gefunden hatte, in welchem alles so restlos klappte. Denn ich war mir klar über die sehr hohe Verantwortung, welche ich übernahm, als ich diese Normen festsetzte. Ich konnte keinen Ausschuß von Sachverständigen hierüber[397] anhören, da ich einstweilen der einzige Sachverständige war. Somit fehlte mir die sonst so gern gewährte kollegiale Hilfe bei der Entdeckung etwaiger Fehler ganz und ich mußte mich auf meine eigene Kritik verlassen. Die durchgehende Harmonie oder Gesetzlichkeit der gefundenen Lösung war eine schwerwiegende Gewähr dafür, daß sie wirklich den gesuchten ausgezeichneten Fall darstellt.
Normung des Farbtonkreises. Die Beendigung des Normungsgeschäftes war nun verhältnismäßig leicht geworden. Die Entwicklung eines farbtongleichen Dreiecks brauchte nur gleicherweise für jeden Farbton durchgeführt zu werden. Werden dann alle Dreiecke im Raum so um eine gemeinsame Achse geordnet, daß sie mit ihren grauen Seiten die Achse berühren und mit der Spitze hinausstreben, so entsteht ein räumliches Gebilde, ein Doppelkegel. Seine obere Spitze ist weiß, die untere schwarz, im Äquator liegt der Vollfarbenkreis. Der obere Kegelmantel enthält die hellklaren Farben, der untere die dunkelklaren, das Innere des Doppelkegels wird von trüben Farben erfüllt. In der Achse liegen die unbunten Farben. Alles erwies sich so wohlgeordnet, daß jede Einzeluntersuchung neue gesetzliche Beziehungen zwischen den Farben aufdeckte, zum Zeichen, daß wirklich das Wesen der Sache getroffen und ausgedrückt war.
Nur ein Punkt verlangte noch Erledigung. Ich hatte anfangs den Farbtonkreis in 100 Grade geteilt, um ganz unvoreingenommen das Ergebnis der gesetzlichen Anordnung der Farbtöne auf mich wirken zu lassen. Die Anschauung ergab zunächst die Zweckmäßigkeit von Herings Annahme der vier Urfarben Gelb, Rot, Blau, Grün, ferner aber die Notwendigkeit, überall je eine Zwischenfarbe einzuschalten. Diese eingeschalteten Farben hatten zwischen Gelb, Rot und Blau schon von jeher eigene Namen. Sie hießen früher Orange und Violett, beides Fremdwörter. Ich ersetzte sie durch Kreß, die[398] Farbe der Kapuzinerkresse und Veil, die Farbe des Veilchens. Dann aber galt es, auch zwischen Blau, Grün und Gelb zwei Farben einzuschalten. Daß man das rötliche Ultramarinblau von seinem grünlichen Nachbar unterscheiden kann oder muß, hatte schon Newton gesehen, als er seinem verunglückten Vergleich mit der Tonleiter zuliebe sieben Farbtöne nötig hatte. Aber ebenso verschieden ist das kalte Seegrün vom warmen Laubgrün, so daß auch das Grün Spaltung gestattet oder verlangt. Dies ergab die Namen Ublau, Eisblau, Seegrün, Laubgrün für die andere Hälfte des Farbtonkreises. Bei der Namengebung habe ich darauf geachtet, daß jeder Name mit einem anderen Buchstaben anfängt, also die einfachste Abkürzung gestattet.
Diese acht Punkte des Farbtonkreises liegen zu weit voneinander, um als Normen auszureichen. Eine entsprechende Untersuchung ergab, daß drei Stufen für jede der acht Hauptfarben notwendig und ausreichend für 99 v.H. aller Anwendungen sind. Das gibt 24 Farbtonnormen mit den Namen erstes, zweites, drittes Gelb, Kreß, Rot usw. Es lassen sich leicht recht genaue anschauliche Erinnerungen mit ihnen verbinden. Man kann mit anderen Worten Farben sehr gut auswendig lernen. Voraussetzung ist nur, daß sie genau definiert sind und einen unverwechselbaren Namen haben, da man sonst nicht weiß, wovon die Rede ist. Das ist wieder ein Beleg für die grundlegende kulturelle Bedeutung des Wortes.
Neben den gesprochenen Namen waren noch kurze Zeichen notwendig. Da die Buchstaben für die Graustufen schon verbraucht waren, blieben hierfür die Ziffern übrig. Am besten wäre gewesen, die Zeichen 0 bis 7 oder 1 bis 8 für die Hauptfarben zu benutzen. Dann aber gab es keine einfachen Bezeichnungen für die Zwischenstufen, welche unendliche Dezimälbrüche wie 1·333 ...[399] und 1·666 ... hätten erhalten müssen: wieder ein Fall, wo sich die Ungeschicklichkeit unserer Zehnerzählung offenbart. So mußte ich die Zahlen 1 bis 24 zur Bezeichnung der 24 Farbtöne wählen; für die seltenen Fälle, wo eine feinere Teilung nötig wird, sind Dezimalen möglich.
Die Farbzeichen. Wenn auch die Einsicht in die Notwendigkeit genauer Farbbezeichnungen für die Ermöglichung einer Farbkultur ein folgenreicher gedanklicher Fortschritt war, so konnte doch ein solcher nicht beginnen, bevor der Gedanke vollständig Gestalt gewonnen hatte. Ich sah also die praktische Aufgabe vor mir, die Ergebnisse der Messung und Normung in eine so handliche Form zu bringen, daß jedermann, selbst ein Kunsthistoriker sie anwenden konnte.
Zwar waren in den Kennzahlen (III, 391), dem zahlenmäßigen Ausdruck der Farbenzerlegung solche eindeutige Bezeichnungen gegeben. Sie waren aber zu allgemein und ließen insbesondere die Normen nicht hervortreten. Die Verhältnisse lagen hier ähnlich wie in der Musik. Ein Ton ist durch seine Schwingzahl der Höhe nach gekennzeichnet, aber um zu wissen, welches Intervall im musikalischen Sinne zwei Töne mit gegebenen Schwingzahlen bilden, bedarf es einer Rechnung, während die Notenschrift dies unmittelbar erkennen läßt. Ein Musikstück, das in Schwingzahlen niedergeschrieben ist, kann deshalb nicht vom Künstler gespielt werden, da es nicht möglich ist, die Rechnungen schnell genug auszuführen, selbst wenn der Künstler die Art der Berechnung lernen wollte, was wiederum nahezu eine Unmöglichkeit bedeutet. Durch die Notenschrift wird es möglich gemacht.
Nun ist die Welt der Töne viel einfacher, als die der Farben. Denn die Tonhöhe hat nur ein Bestimmungsstück, die Schwingzahl. Eine Farbe hat dagegen deren[400] drei: Farbton, Weiß- und Schwarzgehalt. Also muß ein Farbzeichen notwendig aus drei Einzelzeichen bestehen, welche diesen drei Dingen zugeordnet sind.
Im Hinblick auf die eben entwickelten Bedürfnisse habe ich die kurzen Zeichen gewählt, die oben angegeben wurden. Durch ihre Zusammensetzung entstehen die Farbzeichen, die den Noten der Musik entsprechen. Zuerst kommt der Farbton, eine der Zahlen 1 bis 24. Dann kommt der Weißgehalt, einer der Buchstaben c e g i l n p (oder weiter, wenn man weißärmere Farben herstellen kann). Zuletzt kommt der Schwarzgehalt, für den gleichfalls die Buchstaben a c e ... dienen. Durch die Stellung (zuerst oder zuzweit) sind Weiß und Schwarz genügend unterschieden, so daß eine Verwechselung der Bedeutung der Buchstaben ausgeschlossen ist. Beim Weiß hat a den größten Wert, c e g ... haben immer kleinere. Bei Schwarz hat a den Wert Null und c e g ... bedeuten ansteigende Schwarzmengen.
So lernt man bald die Farbzeichen lesen: 13 ni bedeutet z.B. ein erstes Ublau mit wenig Weiß und mittelmäßig viel Schwarz, also ein dunkles, etwas trübes Ultramarinblau.
Der Farbatlas. Obwohl mit den von mir ausgebildeten Geräten die Messung einer Farbe sich in wenigen Minuten erledigen läßt (wobei durchschnittlich Frauen sich geeigneter erwiesen, als Männer), machte ich mir doch klar, daß es zahllose Fälle gibt, wo eine solche Messung nicht tunlich ist. Es war deshalb notwendig, wohlgemessene Farbproben in übersichtlicher Ordnung für den allgemeinen Gebrauch in Gestalt von Karten oder einen Atlas der Farbnormen herzustellen.
Nun sind es zwei ganz verschiedene Dinge, eine vorgelegte Farbe zu messen und eine vorgeschriebene Farbe (die Normfarbe) herzustellen. Es ist ungefähr derselbe Unterschied, wie zwischen einer Längenmessung[401] mit einem Maßstab und der Herstellung eines Maßstabes von genauer Länge. Und da die Farben von drei Elementen abhängen, war die Schwierigkeit hier noch viel größer, als beim Maßstab, der nur eine Veränderliche, die Länge hat.
Tatsächlich befand ich mich einer Aufgabe gegenüber, die bisher noch nie gestellt, also auch nie gelöst war: zahlenmäßig vorher bestimmte Farben herzustellen. Doch war mir dies mehr technische Problem nach der harten Denkarbeit vorher sehr willkommen. Empfand ich doch ausgeprägte Freuden bei der Zusammenstellung der Farbnormen nach ihrer Zusammengehörigkeit. Ich fühlte mich hierbei an die biblische Geschichte von Adam im Paradiese erinnert, wie ihm die verschiedenen Lebewesen vorgeführt wurden und er jedem seinen Namen gab. So war ich immer wieder gespannt, wie diese oder jene durch die Normung geforderte Gruppe von Farben aussehen würde, und fühlte meine Anschauungswelt in glücklichster Weise bereichert, wenn ich z.B. sah, daß die Farben der Gruppe mit dem Weiß- und Schwarzgehalt ge das waren, was die Möbelstoffabrikanten mit couleur Marie Antoinette bezeichneten, nur sehr viel feiner zueinander abgestimmt.
Trotz des schweren Druckes der Kriegszeit gelang es, unter wertvoller Mitarbeit meines Verlegers, Dr. Manitz den ersten gemessenen Farbatlas in etwa zwei Jahren, 1916 und 1917 herzustellen und der Öffentlichkeit zu übergeben. Die Arbeit daran war überaus anstrengend, da bei diesem ersten Vorstoß in die praktische Beherrschung der Farbenwelt natürlich zahllose unvorhergesehene Schwierigkeiten zu überwinden waren und oft Hunderte von gefärbten Blättern verworfen werden mußten. Noch bevor die letzten Tafeln herausgebracht werden konnten, weigerten meine Augen – ich war 64 Jahre alt – den Dienst und ich mußte die letzten Messungen durch einen meiner Söhne machen lassen.[402] Seitdem habe ich sie nur mit Vorsicht gebrauchen dürfen.
Bei der Planung des Atlas waren zum Teil noch die Zwischenstufen gemäß a b c d e f ... beibehalten worden, so daß die Anzahl der eingestellten Farben sich auf über 2500 belief. Das war gewiß eine große und anstrengende Arbeit gewesen. Ich hatte sie aber gern getan, denn zwischen der maßlosen Energievergeudung des Weltkrieges war es mir ein Trost, ja ein Lebensbedürfnis, wenigstens an meinem Teil so viel aufbauende Arbeit zu tun, als ich konnte. Und ich fand wiederum Grund, das unerschütterliche Glück meines lebenslänglichen nahen Verhältnisses zur Wissenschaft zu preisen.
Später habe ich die Herstellung der Farbnormen auf die abgekürzte Reihe a c e g i l n p beschränkt. An dem Dreieck S 396 kann man abzählen, daß 28 bunte Felder (mit Doppelbuchstaben) darin sind. Da jede der 24 Farbtonnormen je ein farbtongleiches Dreieck ergibt, ist die Gesamtzahl der bunten Farbnormen 28 x 24 = 672. Dazu kommen 8 unbunte Normen; insgesamt sind es also 680.
Außer dem Atlas, der aus Karten im Weltformat (III, 301) V, 40 x 56 mm besteht, sind noch andere Zusammenstellungen der Normen hergestellt worden, welche die Übersicht unter bestimmten Gesichtspunkten erleichtern. Hierbei haben sich niemals Schwierigkeiten oder Widersprüche bei der Betrachtung ergeben, so daß auch diese mannigfaltige praktische Erprobung die vollständige Lösung der seinerzeit übernommenen Aufgabe erwiesen hat.
Summa. Betrachte ich rückschauend die Gesamtheit dieser Arbeiten, so halte ich mich für berechtigt, sie als den Höhepunkt meiner wissenschaftlichen Leistungen zu bezeichnen. Hierfür gibt es zwei unabhängige Bewertungsweisen. Die eine bezieht sich auf die Summe geistiger[403] Arbeit, welche zur erfolgreichen Lösung der Aufgabe erforderlich ist, unabhängig von der kulturellen Bedeutung der Lösung. Dies ist der abstrakt wissenschaftliche Standpunkt, bei dem es nur auf das Wie, nicht auf das Was ankommt. Die hierher gehörende Bewertung ist in gewissem Sinne absolut, nämlich unabhängig von den zeitlichen Verhältnissen.
Die andere Bewertung bemißt sich nach dem Einfluß der Lösung auf den Zustand der gegenwärtigen Kultur und wächst und fällt mit diesem. Wenn es beispielsweise gelänge, die Oberfläche des Mondes mit einer Genauigkeit sichtbar zu machen, als ob sie 100 Meter von uns entfernt wäre, so würde diese Leistung einen ganz ungewöhnlichen Betrag von Scharfsinn und Geschicklichkeit beweisen. Aber es läßt sich nicht absehen, welche Bedeutung dies für unsere Kultur haben würde.
Indessen kann sich ein solches Urteil natürlich nur auf die Gegenwart beziehen und man kann theoretisch zugeben, daß vielleicht nach 50 Jahren für uns außerordentlich viel davon abhängen könnte. Als Faraday seine Entdeckungen über elektromagnetische Induktion seinem Hörerkreise vortrug, fragte ihn einer seiner »praktisch« denkenden Zuhörer: wozu ist das nütze? Faraday antwortete: wozu ist ein Kind nütze? Heute beruht die ganze Elektrotechnik, die unser Dasein weitgehend umgestaltet hat und noch viel weiter umgestalten wird, darauf, daß dieses Kind inzwischen herangewachsen ist, dem wir nicht nur die technischen Erfolge verdanken, sondern erheblich vertiefte Einsicht in das Wesen des Lichts und das der Stoffe. Also ist die Beurteilung dieses Wertfaktors viel unsicherer; er ist jedenfalls nicht annähernd absolut zu nennen.
Betrachte ich die Gesamtheit meiner Arbeiten für die Farbenlehre unter diesen beiden Gesichtspunkten, so finde ich beiderseits beträchtliche Werte. Was die[404] denkerisch-wissenschaftliche Seite anlangt, so handelt es sich um ein Problem, welches weder Goethe mit der ungeheuren Kraft seiner Anschauung, noch Helmholtz mit der ungeheuren Kraft seines mathematischen Denkens hatte lösen können. Meine Kräfte stehen nach beiden Richtungen denen jener Heroen weit nach; wie weit, weiß niemand besser als ich. Aber auch ausgezeichnete Köpfe unserer Zeit, die eine Lebensarbeit an das Farbenproblem gewendet hatten, wie Hering (die noch lebenden möchte ich hier nicht nennen) haben versagt. Es handelt sich hier um vielfältige Bedingungen, die gleichzeitig erfüllt sein mußten. Wie eine Kette reißt, wenn nur eines ihrer Glieder schwach ist, wie stark auch die anderen sein mögen, so war zur Lösung dieser Aufgabe ein Zusammentreffen so verschiedenartiger Kenntnisse und Fertigkeiten notwendig, daß schon nach der bloßen Wahrscheinlichkeitsrechnung der günstige Fall nur sehr selten eintreten konnte. Von den vielen Dingen, welche ich in meinem langen Leben ohne bewußten Zusammenhang getrieben hatte, war beinahe jedes nötig, um die Voraussetzungen zu erfüllen, die für das Zustandekommen des Ergebnisses vorhanden sein mußten.
Von solchen Voraussetzungen war die wichtigste die auf angewandter Ordnungswissenschaft (Mathetik) beruhende Kenntnis der Lehre vom Entdecken. Für diese hatte ich nicht nur an eigenen Arbeiten Erfahrungen sammeln können, sondern auch fast ein Menschenalter lang an denen meiner Mitarbeiter und Schüler, unter denen sich Köpfe ersten Ranges befanden. Hierdurch wurde ich in den Stand gesetzt, nicht nur einzelne isolierte Entdeckungen in der Farbenlehre zu machen, sondern eine geschlossene Gruppe aller derer, die nötig waren, um das Endergebnis zu sichern. Während ich dies überdenke, werde ich gewahr, daß sogar der bedenkliche Ausflug in das industrielle Gebiet gelegentlich der Umwandlung[405] des Ammoniaks in Salpetersäure (II, 292) für mich die Schule war, in welcher ich gelernt hatte, Entdeckungen dann zu machen, wenn sie eben nötig waren, da ohne sie die Sache nicht vorwärts zu bringen war.
Was die zweite Seite, die unmittelbare kulturelle Bedeutung anlangt, so brauche ich nur an die Sehnsucht nach Farbe zu erinnern, welche die gegenwärtigen Menschen erfaßt hat, nachdem sie fast zwei Jahrhunderte lang im Trüben gelebt hatten. Dadurch, daß Maß und Zahl in diesem bisher wilden Gebiet zur Herrschaft gebracht worden ist, darf hier eine Entwicklung erwartet werden, die vergleichbar ist der Entwicklung der Chemie, wie sie am Anfang des 19. Jahrhunderts mittels des gleichen Vorgangs, der Ablösung der qualitativen Chemie durch die quantitative, hervorgebracht worden ist. Alle Gebiete, in denen Farbe vorkommt – und wo kommt sie nicht vor! – werden diesen Einfluß erfahren und ich wage nicht die Möglichkeiten auszudenken, die nun Wirklichkeiten werden können. Denn es handelt sich ja um die Physiologie und Psychologie des Auges, des bei weitem wichtigsten unserer Sinnesorgane.
Und dabei habe ich bisher nur die technisch-wissenschaftliche Seite des Fortschritts in Betracht gezogen. Neben dieser gibt es aber noch eine ästhetische, unmittelbar auf das Gefühl gerichtete Seite des Erlebnisses Farbe. Hier handelt es sich in noch viel tieferem Sinne um eine neue Epoche. Ich halte dies für so wichtig, daß ich dafür ein neues Kapitel anfange.
| 1 | Mit bunt bezeichne ich hier und in der Folge jede nicht graue Farbe, die also Gelb, Rot, Blau oder Grün enthält. Die andere Bedeutung des Wortes bunt, nämlich aus verschiedenen Farben zusammen gesetzt, wird hier niemals gebraucht. |
|
Ausgewählte Ausgaben von
Lebenslinien
|
Buchempfehlung
Hoffmann, E. T. A.
Seltsame Leiden eines Theaterdirektors
»Ein ganz vergebliches Mühen würd' es sein, wenn du, o lieber Leser, es unternehmen solltest, zu den Bildern, die einer längst vergangenen Zeit entnommen, die Originale in der neuesten nächsten Umgebung ausspähen zu wollen. Alle Harmlosigkeit, auf die vorzüglich gerechnet, würde über diesem Mühen zugrunde gehen müssen.« E. T. A. Hoffmann im Oktober 1818
88 Seiten, 5.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Geschichten aus dem Biedermeier. Neun Erzählungen
Biedermeier - das klingt in heutigen Ohren nach langweiligem Spießertum, nach geschmacklosen rosa Teetässchen in Wohnzimmern, die aussehen wie Puppenstuben und in denen es irgendwie nach »Omma« riecht. Zu Recht. Aber nicht nur. Biedermeier ist auch die Zeit einer zarten Literatur der Flucht ins Idyll, des Rückzuges ins private Glück und der Tugenden. Die Menschen im Europa nach Napoleon hatten die Nase voll von großen neuen Ideen, das aufstrebende Bürgertum forderte und entwickelte eine eigene Kunst und Kultur für sich, die unabhängig von feudaler Großmannssucht bestehen sollte. Dass das gelungen ist, zeigt Michael Holzingers Auswahl von neun Meistererzählungen aus der sogenannten Biedermeierzeit.
- Georg Büchner Lenz
- Karl Gutzkow Wally, die Zweiflerin
- Annette von Droste-Hülshoff Die Judenbuche
- Friedrich Hebbel Matteo
- Jeremias Gotthelf Elsi, die seltsame Magd
- Georg Weerth Fragment eines Romans
- Franz Grillparzer Der arme Spielmann
- Eduard Mörike Mozart auf der Reise nach Prag
- Berthold Auerbach Der Viereckig oder die amerikanische Kiste
434 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum