Axonometrie
[421] Axonometrie nennt man das Projektionsverfahren, das ein parallel-perspektivisches Bild eines Körpers vermittelst der Koordinaten seiner Punkte liefert. Man unterscheidet dabei zwischen der rechtwinkligen und schiefwinkligen Axonometrie, je nachdem die projizierenden Strahlen zur Bildebene senkrecht stehen oder nicht.
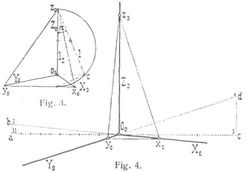
In beiden Fällen liegt dem Projektionsverfahren ein Koordinatensystem zugrunde, dessen Koordinatenebenen aufeinander senkrecht stehen und der Grundriß-, Aufriß- und Seitenrißebene der gewöhnlichen orthogonalen Projektion entsprechen. Die drei Koordinatenebenen schneiden[421] sich nach dreien aufeinander senkrecht stehenden Geraden, den Koordinatenachsen; letztere bilden das Achsenkreuz. In Fig. 1 ist Grundriß, Aufriß und Seitenriß eines Punktes a samt seinen Koordinaten, bezogen auf das Koordinatensystem X, Υ, Z in rechtwinkliger Projektion dargestellt. Fig. 2 gibt das entsprechende axonometrische Bild hierfür. Die Linien X0 Υ0 Z0 sind die axonometrischen Koordinatenachsen, sie bestimmen das axonometrische Bild des Achsenkreuzes. Die Strecken o0ax, o0ay, o0az sind die axonometrischen Koordinaten des Punktes a, durch sie ist dessen axonometrisches Bild a0 konstruierbar. Die Punkte a1, a2, a3, in Fig. 2 stellen den axonometrischen Grund-, Auf- und Seitenriß des Punktes a beziehungsweise dar. Zwischen den axonometrischen und den wirklichen Koordinaten eines Punktes bestehen die Verhältnisse o0ax/oax, o0ay/oay, o0az/oaz ihre absoluten Werte sind kleiner als die Einheit und hängen lediglich von der Größe der Neigungswinkel αß, γ der Achsen X, Υ, Z gegen die Bildebene ab; sie heißen die Verkürzungsverhältnisse der axonometrischen Projektion und sind bestimmt, sobald das axonometrische Bild des Achsenkreuzes gegeben ist. Die drei Koordinatenebenen schneiden die Bildebene nach einem Dreieck, x0 y0 z0 (s. Fig. 3), dessen Seiten auf den Achsenbildern X0 Y0 Z0, bezw. senkrecht stehen. Hiernach bestimmen sich die Winkel α, β, γ und die Verkürzungsverhältnisse lx/l = cosα, y/l = cosß, lz/l = cos γ, wenn l die Länge einer von dem Koordinatenanfangspunkte o auf den Achsen X, Υ, Z ausgetragenen Strecke bezeichnet. Sind die Verkürzungsverhältnisse ermittelt, so bestimmen sich mittels derselben aus den wirklichen Koordinaten eines Punktes dessen axonometrische Koordinaten, woraus sich dann das axonometrische Bild des Punktes konstruieren läßt. Kennt man aber die Verkürzungsverhältnisse, was in der Regel der Fall ist, so bestehen auf Grund elementarer geometrischer Betrachtungen [1] eine Reihe von Konstruktionen für das axonometrische Bild des Achsenkreuzes. Die bequemste Konstruktion ist wohl die folgende: Mit drei Größen m, n, p, den Verhältniszahlen, die sich zueinander verhalten wie die Verkürzungsverhältnisse, bildet man die Werte m2, n2, p2 und mit diesen als Seitenlängen ein Dreieck; dann fallen dessen innere Halbierungslinien mit den Achsenbildern der zugehörigen axonometrischen Projektion zusammen.
Als besondere axonometrische Projektionsarten sind gebräuchlich: 1. die trimetrische oder anisometrische Projektion, die Größen m, n und p sind voneinander verschieden; gebräuchliche Werte der Verhältniszahlen sind m : n : p = 9/10 : 1/2 : 1; 2. die dimetrische oder monodimetrische Projektion, es ist m = p in der Regel m : n : p = 1 : 1/2 : 1; 3. die isometrische Projektion, es ist m = n = p.
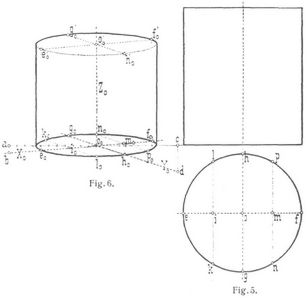
Anisometrische oder trimetrische Projektion: Das Achsenkreuz im Raume hat gegen die Bildebene eine ganz allgemeine Lage und kann demgemäß auch das Bild des Achsenkreuzes innerhalb gewisser Grenzen beliebig gewählt werden. Bedingung hierfür ist nur, daß der Winkel zwischen je zwei Achsenbildern ein stumpfer sein muß. Die Verkürzungsverhältnisse bezw. die Achsenmaßstäbe bestimmen sich hieraus. Für die oben erwähnte trimetrische Projektion mit den Verhältniszahlen m = 9/10 n = 5/10 und p = 1 hat man folgende einfache und zweckmäßige Konstruktion des Achsenkreuzes: Man trägt (s. Fig. 4) auf einer Geraden der Strecke O0a = 11 Einheiten ab, errichtet ab senkrecht zu O0a = 1, so gibt die Verbindungslinie O0b, die X0-Achse; macht man in gleicher Weise die Strecke O0c in der Verlängerung von O0a gleich 3 Einheiten, die Senkrechte cd zu O0c = 1, so liefert die Verbindungslinie O0d das Achsenbild Y0; das Achsenbild Z0 steht senkrecht zu aO0c. Bei der Herstellung eines trimetrischen Bildes eines Körpers überträgt man nunmehr für jeden Punkt des Körpers die Z-Koordinaten unverkürzt, die Y-Koordinaten auf die Hälfte, die X-Koordinaten aber auf 9/10 verkürzt als axonometrische Koordinaten des Punktes. So ist z.B. in Fig. 6 die trimetrische Projektion eines senkrechten Kreiszylinders (Fig. 5) dargestellt, und es ist[422]
o0e0 = o0f0 = 9/10oe (Fig. 5), desgleichen
o0i0 = o0m0 = 9/10oi = 9/10om (Fig. 5) und
o0g0 = o0h0 = 1/2og = 1/2oh (Fig. 5), ebenso
i0k0 = i0l0 = m0n0 = m0p0 = 1/2ik = 1/2il (Fig. 5) u.s.w.; endlich ist o0o0' = der Höhe des Zylinders.
Die obere elliptische Abgrenzung des trimetrischen Zylinderbildes ergibt sich durch Ziehen von Mantellinien durch die Punkte e0 bis p0 und Abtragen der Zylinderhöhe auf denselben.
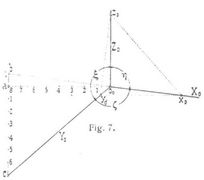
Dimetrische Projektion: Zwei Achsen, in der Regel die X- und die Z-Achse, sind gegen die Bildebene unter dem gleichen Winkel geneigt, weshalb alle zu diesen Achsen parallelen Strecken im Bilde sich in dem gleichen Verhältnisse verkürzen. Das Dreieck x0 γ0 z0 (Fig. 7), nach dem die Achsenebenen XY, YZ und ZX die Bildebene schneiden, ist gleichschenklig. Jedes gleichschenklig spitzwinklige Dreieck kann als ein Spurendreieck der Bildebene für eine dimetrische Projektion aufgefaßt werden; es gibt also unzählig viele Lagen des Achsenkreuzes, die einer dimetrischen Projektion entsprechen. Für die gebräuchlichste dimetrische Projektion, bei der m : n : p = 1 : 1/2 : 1 ist, ergibt sich das Bild des Achsenkreuzes am bequemsten wie folgt: Man macht (s. Fig. 7) o0a = 8, ab = 1 und ac = 7, dann liefern die Verbindungslinien o0b und o0c die Achsenbilder X0 und Y0, während Z0 auf o0a senkrecht steht. Bei der Herstellung des dimetrischen Bildes eines Körpers sind für jeden Punkt desselben die X- und Z-Koordinaten unverkürzt zu lassen, die Y-Koordinaten aber um die Hälfte zu verkleinern. So ist z.B. in Fig. 9 die dimetrische Projektion eines senkrechten Kreiskegels (s. Fig. 8) dargestellt; es ist dabei o0s0 = o2s2, o0a0 = o1a1, o0c0 = 1/2o1c1 u.s.w.
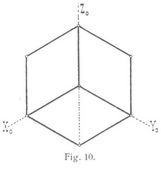
Isometrische Projektion: Alle drei Achsen X, Υ, Z haben gegen die Bildebene gleiche Neigung, es ist m = n = p. Die drei Koordinaten eines Punktes verkürzen sich gleichviel. Bei der Herstellung eines axonometrischen Bildes eines Körpers überträgt man die Koordinaten eines Punktes unverkürzt; als axonometrische Koordinaten in das Bild des Körpers. So ist in Fig. 10 das isometrische Bild eines Würfels dargestellt. Der Umriß dieses Bildes ist ein regelmäßiges Sechseck; hierbei ist die Seite des Sechsecks gleich der Länge der Würfelkante abzutragen.
Zur Herstellung des axonometrischen Bildes eines Körpers eignet sich am besten die schiefwinklige Axonometrie, weil bei ihr das axonometrische Bild des Achsenkreuzes beliebig wählbar ist und außerdem auch die Verkürzungsverhältnisse willkürlich angenommen werden dürfen [2]. Am gebräuchlichsten ist auch hier die isometrische Projektion m = n = p = 1. Die Axonometrie dient auch als selbständige Projektionsmethode, mittels der sich alle darstellend geometrischen Aufgaben, die sich auf Lagen- und Größenverhältnisse beziehen, direkt, d.h. ohne Transformation, auf den rechtwinkligen Grund- und Aufriß lösen lassen, sobald bei der rechtwinkligen Axonometrie das Bild des Achsenkreuzes gegeben ist, bei der schiefwinkligen aber noch außerdem die Verkürzungsverhältnisse gewählt und [3].
Literatur: [1] Vonderlinn, Lehrbuch des Projektionszeichnens, Stuttgart 1892, III, 2. – [2] Pelz, Zur wissenschaftlichen Behandlung der orthogonalen Axonometrie, Sitzungsberichte der K. Akademie der Wissenschaften, Wien 1880–84. – [3] Pohlke, Darstellende Geometrie, Berlin 1860, 1. Abteilung.
Vonderlinn.
Buchempfehlung
Stifter, Adalbert
Die Mappe meines Urgroßvaters
Der Erzähler findet das Tagebuch seines Urgroßvaters, der sich als Arzt im böhmischen Hinterland niedergelassen hatte und nach einem gescheiterten Selbstmordversuch begann, dieses Tagebuch zu schreiben. Stifter arbeitete gut zwei Jahrzehnte an dieser Erzählung, die er sein »Lieblingskind« nannte.
156 Seiten, 6.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Geschichten aus dem Biedermeier. Neun Erzählungen
Biedermeier - das klingt in heutigen Ohren nach langweiligem Spießertum, nach geschmacklosen rosa Teetässchen in Wohnzimmern, die aussehen wie Puppenstuben und in denen es irgendwie nach »Omma« riecht. Zu Recht. Aber nicht nur. Biedermeier ist auch die Zeit einer zarten Literatur der Flucht ins Idyll, des Rückzuges ins private Glück und der Tugenden. Die Menschen im Europa nach Napoleon hatten die Nase voll von großen neuen Ideen, das aufstrebende Bürgertum forderte und entwickelte eine eigene Kunst und Kultur für sich, die unabhängig von feudaler Großmannssucht bestehen sollte. Dass das gelungen ist, zeigt Michael Holzingers Auswahl von neun Meistererzählungen aus der sogenannten Biedermeierzeit.
- Georg Büchner Lenz
- Karl Gutzkow Wally, die Zweiflerin
- Annette von Droste-Hülshoff Die Judenbuche
- Friedrich Hebbel Matteo
- Jeremias Gotthelf Elsi, die seltsame Magd
- Georg Weerth Fragment eines Romans
- Franz Grillparzer Der arme Spielmann
- Eduard Mörike Mozart auf der Reise nach Prag
- Berthold Auerbach Der Viereckig oder die amerikanische Kiste
434 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum