Belastung [2]
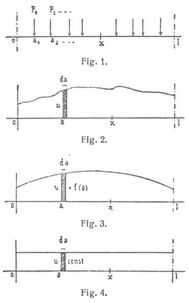
[661] Belastung der Träger (s.a. Angreifende Kräfte, Eigengewicht, Verkehrslast). Dieselbe kann aus konzentrierten Lasten und stetig verteilten Lasten bestehen. Bei edleren sind die Angriffspunkte durch meßbare Strecken getrennt (Fig. 1 und 10), bei letzteren bilden sie eine stetige Folge (Fig. 2–9). Die stetig verteilte Last heißt auf einer Strecke gesetzmäßig verteilt, wenn sich für alle Elemente der Strecke die Belastung pro Längeneinheit durch dieselbe Gleichung, u = f(a), das Gesetz der Verteilung, ausdrücken läßt; sie heißt im besonderen gleichmäßig verteilt, wenn die Belastung pro Längeneinheit konstant ist. Trägt man bei beliebiger stetig verteilter Last an jeder Stelle a die Belastung pro Längeneinheit daselbst als Ordinate an, so entsteht in der Verbindungsgeraden der Endpunkte die entsprechende Belastungslinie; die Fläche zwischen dieser und der Abszissenachse wird Belastungsfläche genannt. In Fig. 2–4 sind die Belastungslinien für eine beliebige stetig verteilte Last, eine gesetzmäßig verteilte Last und eine gleichmäßig verteilte Last verzeichnet. Als Verkehrslast bezeichnet man diejenigen Lasten, die der Träger neben dem Eigengewicht der[661] Konstruktion aufzunehmen hat. Eigengewicht und Verkehrslast zusammen bilden die Gesamtbelastung (Vollbelastung, Totalbelastung). Da die Verkehrslast in der Regel ganz oder teilweise ihren Ort wechseln kann, so pflegt man auch von fester Last und bewegter Last zu sprechen, die vereint ebenfalls die Gesamtbelastung ausmachen. Von der Belastungsart eines Trägers spricht man im Hinblick auf das Vorkommen konzentrierter, gesetzmäßig und gesetzlos verteilter Latten (man fragt, wie die Lasten wirken); der Ausdruck Belastungsfall dagegen bezieht sich auf die Anordnung der Lasten am Träger (man fragt, wo die Lasten wirken). Zu vollständiger Berechnung eines Brückenträgers hat man oft eine ganze Anzahl von Belastungsfällen zu berücksichtigen (s. z.B. Balken, durchlaufende). Da aber auch verschiedene Belastungsarten vorkommen, so hat man die Formeln zur Berechnung der wichtigsten Träger zunächst für ganz beliebige Belastungen gegeben, wonach sich dieselben für besondere Belastungen leicht spezialisieren lassen, indem je nach der Belastung nur diejenigen Glieder (Summenausdrücke Σ) besondere Formen annehmen, die eben die Lasten enthalten. Dabei ist zu beachten, daß eine stetig verteilte Last von u = f(a) pro Längeneinheit für die Strecke d a die unendlich kleine konzentrierte Last ergibt (Fig. 2–4):
P = u d a = f (a) d a,
und eine Summe solcher unendlich kleiner Summanden als Integral bezeichnet wird, so daß z.B.
und speziell für gleichmäßig verteilte Last, d.h. bei konstantem u,
Dabei in wie im folgenden vorausgesetzt, daß die Summengrenzen als Abszissen aufzufassen sind (vgl. Balken, Bogen). Es möge nun auf die wichtigsten Fälle hingewiesen werden.
I. Gleichmäßig verteilte Last. Die Belastung sei innerhalb der Summengrenzen auf die ganze Länge gleichmäßig verteilt, u pro Längeneinheit. Dann erhält man in der angeführten Weise:
Hieraus ergeben sich auch bei beliebigen l, μ, d:
Weiter kommen mitunter zur Verwendung:
und wenn
[662] Die Berechnung kann oft durch Zerfällung umgangen oder erleichtert werden. So ist
Näheres s. insbesondere [5], S. 14, 29 und [6], S. 2.
II. Konzentrierte Lasten und gleichmäßig verteilte Last. Es sei innerhalb der Summengrenzen u die gleichmäßig verteilte Last pro Längeneinheit (gewöhnlich das Eigengewicht). Die von ihr herrührenden Teile der Summenwerke Σ sind aus I zu entnehmen. Beziehen sich im folgenden die Summen rechts nur noch auf die konzentrierten Laden, während diejenigen links alle Lassen umfassen, so hat man:
III. Zweierlei gleichmäßig verteilte Lasten. Die gleichmäßig verteilte Last sei (Fig. 5, 6):
u von a = 0 bis a = z, u' von a = z bis a = l,
dann hat man auf die Länge d a:
von 0 bis z P = u d a, von z bis l P = u' d a,
wonach für
und für
In gleicher Weise laden sich die sonst vorkommenden Summen spezialisieren. In praktischen Fällen pflegen u, u' das Eigengewicht und die Gefamtbelastung pro Längeneinheit zu sein, so daß ± (u' – u) = p die Verkehrslast pro Längeneinheit bedeutet. Näheres s. insbesondere [1], S. 70, [5], S. 14, [6], S. 2, und [7], § 13.
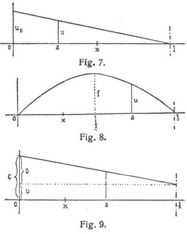
IV. Beliebig gesetzmäßig verteilte Lasten. Die Werte der Summenausdrücke ergeben sich in der obenangeführten Weise. Wäre z.B. die Belastung pro Längeneinheit nach der Andeutung in Fig. 7 veränderlich, dann hätte man bei a
u = (l–a)u0/l, P = u d a,
womit
und sollte u entsprechend Fig. 8 durch die Parabelgleichung
u = a(l–a)4f/l2
ausgedrückt sein, so würde wieder mit P = u d a:
Die Resultate gelten natürlich auch für x = 0 oder l. Mit den Ausdrücken für die gleichmäßig verteilte Last und die Dreieckslast hat man auch diejenigen für die Trapezlad, die sich aus jenen beiden zusammensetzen läßt, so daß bei den Bezeichnungen in Fig. 9
Näheres s. insbesondere [5], S. 14, [6], S. 2.
V. Konzentrierte Lasten bei veränderlichem x (bei verschiedenen Querschnitten). Mitunter hat man Summen der unter I. behandelten Art bei konstanten a (bestimmter Laststellung) und variabeln x zu differenzieren oder zu integrieren. Für Differentiationen gilt die Formel:
so daß einfach die mit P multiplizierte Funktion φ (x, a) nach x zu differentiieren ist. Beispielsweise wird
Für Integrationen hat man
wonach beispielsweise
Näheres s. insbesondere [5], S. 12, [S]. 1.[663]
VI. Konzentrierte Lasten bei veränderlichem a (bei verschiedenen Stellungen). In manchen Fällen sind Summen der unter I. erwähnten Art bei konstantem x, aber variablem a zu differentiieren. Bewegt sich ein System von Lassen P1 P2, ... in festen Entfernungen (Lastzug, z.B. Fig. 10) zwischen den Summengrenzen, so ändern sich mit jeder unendlich kleinen. Verrückung alle a um das gleiche d a, es ergibt sich:
so daß jetzt die mit P multiplizierte Funktion φ (x, α) einfach nach a zu differentiieren ist. Beispielsweise erhält man
und allgemeiner bei konstantem n:
Näheres s. insbesondere [5], S. 16, [6], S. 4.
S.a. Schnittkräfte (Einfluß der Zwischenträger), Lastäquivalente, Eigengewicht Verkehrslast.
Literatur: [1] Weyrauch, Allgemeine Theorie und Berechnung der kontinuierlichen und einfachen Träger, Leipzig 1873, S. 70, 167. – [2] Ders., Zeitschr. f. Mathem. und Physik 1873, S. 396, und 1874, S. 547. – [3] Ders., Zeitschr. d. Archit.- und Ingen.- Vereins zu Hannover 1875, S. 467. – [4] Ders., Aufgaben zur Theorie elastischer Körper, Leipzig 1885, S. 2. – [5] Ders., Theorie der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1887, S. 9. – [6] Ders.,. Beispiele und Aufgaben zur Theorie der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1888, S. 1. – [7] Ders., Elastische Bogenträger, München 1895, § 13.
Weyrauch.
Buchempfehlung
Aristoteles
Physik
Der Schluß vom Allgemeinen auf das Besondere, vom Prinzipiellen zum Indiviudellen ist der Kern der naturphilosophischen Lehrschrift über die Grundlagen unserer Begrifflichkeit von Raum, Zeit, Bewegung und Ursache. »Nennen doch die Kinder zunächst alle Männer Vater und alle Frauen Mutter und lernen erst später zu unterscheiden.«
158 Seiten, 8.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Geschichten aus dem Biedermeier II. Sieben Erzählungen
Biedermeier - das klingt in heutigen Ohren nach langweiligem Spießertum, nach geschmacklosen rosa Teetässchen in Wohnzimmern, die aussehen wie Puppenstuben und in denen es irgendwie nach »Omma« riecht. Zu Recht. Aber nicht nur. Biedermeier ist auch die Zeit einer zarten Literatur der Flucht ins Idyll, des Rückzuges ins private Glück und der Tugenden. Die Menschen im Europa nach Napoleon hatten die Nase voll von großen neuen Ideen, das aufstrebende Bürgertum forderte und entwickelte eine eigene Kunst und Kultur für sich, die unabhängig von feudaler Großmannssucht bestehen sollte. Michael Holzinger hat für den zweiten Band sieben weitere Meistererzählungen ausgewählt.
- Annette von Droste-Hülshoff Ledwina
- Franz Grillparzer Das Kloster bei Sendomir
- Friedrich Hebbel Schnock
- Eduard Mörike Der Schatz
- Georg Weerth Leben und Taten des berühmten Ritters Schnapphahnski
- Jeremias Gotthelf Das Erdbeerimareili
- Berthold Auerbach Lucifer
432 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum
![Belastung [2]](/Lueger-1904.images/I/TL010945.jpg?w=166&h=59&vid=179561937)
![Belastung [2]](/Lueger-1904.images/I/TL011269.jpg?w=166&h=81&vid=1861677235)