Online-Bibliothek

Träger [1]

[585] Träger. Ein Träger ist ein materielles System (s. Bd. 6, S. 333), welches zur Aufnahme und Uebertragung von Lasten und andern äußeren Aktivkräften auf außerhalb desselben gelegene Stützen dient (vgl. Spannweite, Aktivkräfte, Belastung der Träger, Eigengewicht, Verkehrslast, Winddruck, Lastäquivalente u.s.w.).

Unter dem Einflusse jener äußeren Kräfte und andrer Ursachen entstehen bei allen Trägern innere Kräfte und als weitere äußere Kräfte (Bd. 1, S. 103; Bd. 6, S. 333) Stützenreaktionen. Der Träger S kann aus mehreren Trägerstücken oder Scheiben bestehen, solchen Teilsystemen s (Bd. 6, S. 333), zwischen welchen infolge konstruktiver Mittel resultierende Kräfte von bekanntem Angriffspunkte, bekannter Richtung oder bekannter Größe wirken. Je nach der Anzahl und Anordnung der Auflager (Bd. 1, S. 354) und Scheiben unterscheidet man verschiedene Trägerarten (vgl. Balken, Bogen, Ketten, Gelenkträger, Hängebrücken, Hängewerke, Sprengwerke u.s.w.); der Verlauf der Begrenzung oder Achse gibt Veranlassung zur Unterscheidung verschiedener Trägerformen (vgl. Parallelträger, Dreiecksträger, Trapezträger, Parabelträger, Halbparabelträger, Ellipsenträger, Schwedlerträger u.s.w.) und die Gliederung der Scheiben zur Unterscheidung verschiedener Trägersysteme (vgl. Blechträger, Gitterträger, Fachwerke einfachen und mehrfachen Systems, Ständerfachwerke, Strebenfachwerke, Gewölbe u.s.w.) Ebene Träger sind dadurch charakterisiert, daß sämtliche äußere Kräfte und die mit ihnen ins Gleichgewicht tretenden Resultanten der inneren Kräfte (z.B. die Stabkräfte eines Fachwerks) in einer Ebene liegen. Alle statischen Untersuchungen lassen sich dann auf diese Trägerebene beschränken, welche bei Berücksichtigung des Eigengewichts nur eine Vertikalebene sein kann. In letzterem Falle heißen die Horizontalabstände zwischen unmittelbar aufeinander folgenden Stützpunkten Spannweiten (s.d.) oder Oeffnungen (s.d.), die Zwischenstützen Pfeiler, die Endstützen Widerlager. Der Träger ist ein einfacher Träger oder ein durchlaufender Träger (kontinuierlicher Träger), je nachdem er sich nur über eine Oeffnung oder aber ungetrennt über zwei und mehr Oeffnungen erstreckt (vgl. Balken, einfache und durchlaufende, Bd. 1, S. 503, 507, 518; Bogen, einfache und durchlaufende, Bd. 2, S. 141, 153, 155). Ueber räumliche Träger s. Fachwerk (Bd. 3, S. 533), Pfeiler der Brücken (Bd. 7, S. 83), Kuppeldach (Bd. 2, S. 496), Klostergewölbe (Bd. 4, S. 500, 508), Kreuzgewölbe (Bd. 4, S. 500, 507) u.s.w. Auch ganze Brückenjoche, Dachstühle u.s.w. sind als räumliche Träger anzusehen.

Eine Trägerart heißt statisch bestimmt oder statisch unbestimmt, je nachdem bei bekannten äußeren Aktivkräften (Lasten u.s.w.) und Gleichgewichtslagen der Scheiben[585] sämtliche äußere Kräfte der letzteren durch die Statik allein bestimmt sind oder nicht; sie heißt stabil oder labil, je nachdem, abgesehen von elastischen Formänderungen, die relative Lage der Scheiben zueinander und zu den Stützen eine feste oder mit den äußeren Kräften veränderliche ist. Im allgemeinen hat der Ingenieur stabile Konstruktionen herzustellen, so daß bei Anwendung labiler Träger (z.B. Ketten) besondere Versteifungsträger nötig werden (vgl. Hängebrücken, Bd. 4, S. 710, 718). – Die Stützenreaktionen eines Trägers mit n Stützen sind vollständig bestimmt durch ihre Angriffspunkte, Richtungen und Größen, also für die im folgenden vorausgesetzten ebenen Träger durch je zwei Komponenten und ein Moment. Zur Ermittlung dieser 3 n Größen hat man zunächst die drei Gleichgewichtsbedingungen der Ebene, welchen die am ganzen Träger wirkenden äußeren Kräfte genügen müssen (Bd. 6, S. 333). Soll nun die Trägerart statisch bestimmt sein, so sind konstruktive Anordnungen bezüglich der Auflager und Zerfällung in Scheiben derart zu treffen, daß die übrigen 3 (n – 1) Größen bekannt oder durch neue statische Gleichungen bestimmt werden. Dies ist durch verschiedene Mittel erreichbar; die gewöhnlichsten sind Gelenke (Schnittmoment in Hinsicht des Gelenkmittelpunkts gleich Null) und Gleitungen (Reaktionskomponente senkrecht zur Bahn gleich Null). Vgl. Auflager (Bd. 1, S. 354), Gelenke bei Ingenieurkonstruktionen (Bd. 4, S. 358) und Schnittkräfte, Schnittmomente (Bd. 7, S. 768). Bei statisch unbestimmten Trägerarten sind die Stützreaktionen nur unter Mitverwendung außerstatischer Beziehungen bestimmbar, welche die Elastizitätslehre liefert. Vgl. Balken und Bogen, Fachwerke (statisch unbestimmte), Hängewerke, Sprengwerke, Träger (zusammengesetzte), Verschiebungsarbeit u.s.w.

Für einen beliebigen ebenen Träger von s Scheiben mögen die Stützenreaktionen durch r, die Zwischenreaktionen (der Scheiben gegeneinander) durch z voneinander unabhängige Größen bestimmt sein. Dann bestehen folgende Bedingungen ([12], S. 6):

für stabile Trägerarten 3 s < r + z

1.

für statisch bestimmte Trägerarten 3 s r + z

2.

also für statisch bestimmte und stabile Trägerarten 3 s = r + z.

3.

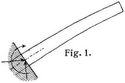
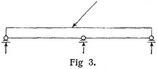
Zur Festlegung des Trägers gegen die Stützen muß mindestens r = 3 sein (Beispiele Fig. 1, 2, 5 u. f w.). Die Erfüllung der Bedingung 1. oder 2. genügt jedoch nicht, eine Trägerart stabil oder statisch bestimmt zu machen, es kommt nicht nur auf die Anzahl, sondern auch auf die Anordnung jener unabhängigen Reaktionselemente an. So entsprechen sowohl Fig. 1 und 2 als Fig. 3 wegen s = 1, r = 3, z = 0 der Bedingung 3.; trotzdem sind nur die Trägerarten Fig. 1 und 2 statisch bestimmt und stabil, die Trägerart Fig. 3 dagegen statisch unbestimmt und labil, jede nicht vertikale Kraft würde den Träger Fig. 3 über die Stützen wegschieben. Auch die Trägerart Fig. 4 erfüllt mit s = 3, r = 5, z = 4 die Bedingung 3., während der Träger rechts labil, links statisch unbestimmt ist. Es gilt nun der Satz: Eine Trägerart, welche bei s Scheiben r + z = 3 s wirksame Reaktionskomponenten besitzt, die sich für die vorkommenden Belastungen u.s.w. aus statischen Bedingungsgleichungen bestimmen lassen, ist für diese Belastungen u.s.w. statisch bestimmt und stabil. Vgl. [12], S. 7, und Bd. 3, S. 535. So ist z.B. die Trägerart Fig. 2 für die gewöhnlichen (vertikal nach abwärts gerichteten) Aktivkräfte stabil, sie wäre aber labil für Aktivkräfte, welche rechts eine von oben nach unten wirkende Reaktion erforderten, es sei denn, daß durch geeignete Verankerung des Trägerendes die Möglichkeit solcher Reaktionen geboten würde. Der Fall kommt beispielsweise bei dem Träger Fig. 2 als Versteifungsbalken von Hängebrücken vor (Bd. 4, S: 713).

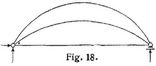
Fassen wir nun noch einige spezielle Fälle ins Auge, wobei auch solche berücksichtigt werden sollen, welche nicht in besonderen Artikeln behandelt sind. Die Trägerart mit einem festen und einem in beliebiger Richtung frei verschiebbaren Gelenkauflager Fig. 2, 5 ist statisch bestimmt und stabil. Gewöhnlich ist die Verschiebung horizontal (Fig. 2, vgl. Balken, Bd. 1, S. 519; Balkenfachwerke, Parallelträger, Dreiecksträger, Trapezträger, Parabelträger, Halbparabelträger, Ellipsenträger, Schwedlerträger, Paulische Träger, Polonceauträger, Bogen mit Zugstange, Bogensehnenträger, Hängewerke u.s.w.), doch wurde behufs Materialersparnis auch der Träger mit schief verschiebbarem Auflager unter gewissen Voraussetzungen empfohlen ([6], S. 25, [8], S. 127), über seine Berechnung s. [12], S. 289, 291, 295; [13], S. 464, 466, 469. Sind außer dem festen Gelenkauflager mehrere in gleicher Richtung frei verschiebbare vorhanden (Fig. 6), so ist die Trägerart zwar stabil, aber ebenso vielfach statisch unbestimmt (man hat ebensoviel Reaktionselemente zuviel), als Zwischenstützen vorhanden sind (vgl. Balken, Bd. 1, S. 505, 508, Parallelträger u.s.w.). Werden jedoch an geeigneten Stellen (z.B. entsprechend Fig. 7, nicht Fig. 4) eine Anzahl Zwischengelenke[586] gleich der Zahl der Zwischenstützen eingeschaltet, so entsteht eine statisch bestimmte Trägerart (vgl. Gelenkträger, Bd. 4, S. 361). Auch die Trägerarten Fig. 8 und 9 sind statisch bestimmt und stabil. Die Trägerart Fig. 10 ist einfach statisch unbestimmt und diejenige Fig. 11 zweifach statisch unbestimmt (vgl. Balken, Bd. 1, S. 505, 520), während von den Trägerarten Fig. 12–15 die erste dreifach, die zweite zweifach, die dritte einfach statisch unbestimmt, die vierte aber mit s = 2, r = 4, z = 2 statisch bestimmt ist (vgl. Bogen, Bd. 2, S. 155), Bogenfachwerke, Bd. 2, S. 161; bezüglich Fig. 13 [30] u.s.w. Anstatt des reellen Zwischengelenks in Fig. 15 kann, wie in andern Fällen, auch ein imaginäres Gelenk angeordnet werden (Fig. 16, vgl. Bd. 4, S. 368, [7], [8], S. 40), Berechnung des so entstehenden Trägers s. [12], S. 296, [13], S. 471, 472 über andre Träger mit imaginären Gelenken s. Bd. 4, S. 357, 363; [8], S. 40, 115, 123, 131). Im Gegensatz zu der Trägerart Fig. 14, deren Horizontalschub (s.d.) mittels der Elastizitätslehre bestimmt werden muß, ist der Träger mit konstantem Horizontalschub (Fig. 17), welcher für die Elbbrücke bei Riesa (Techn. Blätter 1880, S. 86) zur Ausführung kam, bezüglich der äußeren Kräfte statisch bestimmt ([1], [4], [10], II, S. 216), seine Berechnung s. [12], S. 268, 271, [13], S. 411. Auch der Bogen mit Zugstange Fig. 18 (Bd. 2, S. 175), Bogensehnenträger (Bd. 2, S. 176) und Mittengelenkbalken (Bd. 6, S. 449) sind von statisch bestimmter Art, sie besitzen wie Fig. 2 bei 5 = 1 ein festes und ein horizontal verschiebbares Gelenkauflager.

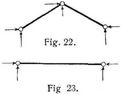
Während alle bisher angeführten Trägerarten stabil waren, stellen Fig. 19 und 20 einfach labile Trägerarten und Fig. 21 bei s Stäben mit r = 4, z = 2 (s – 1) eine (s – 2)-fach labile Trägerart dar (man hat s – 2 Reaktionselemente zuwenig), welche dabei statisch bestimmt sind. Für s = 2 führt Fig. 21 auf die stabile Trägerart Fig. 15, 22, für s = 1 auf die einfach statisch unbestimmte Trägerart Fig. 14, 23. Wenn im Falle der Fig. 21 die Gelenke stetig aufeinander folgen, so hat man trotz ∞-facher Labilität noch immer eine statisch bestimmte Trägerart (vgl. Ketten, Kettenlinien, Bd. 5, S. 448, Naviersche Kettenbrückenlinie, Bd. 6, S. 589, Hängebrücken, Bd. 4, S. 710, u.s.w.). Von den Trägerarten Fig. 24–26 ist die erste statisch bestimmt stabil (s = 4, r = 6, z = 6), die zweite stabil und einfach statisch unbestimmt (s = 3, r = 6, z = 4), die dritte stabil und dreifach statisch unbestimmt (s = 1, r = 6, z = 0, vgl. Bogen, durchlaufende, Bd. 2, S. 153, Bogenfachwerke, Bd. 2, S. 167, und Hängebrücken, feste, Bd. 4, S. 726). Bei m Zwischenstützen ist die Trägerart Fig. 26 (m + 1)-fach statisch unbestimmt, gegenüber Fig. 6 kommt nur der Horizontalschub hinzu. Fig. 27 und 28 stellen statisch bestimmte Trägerarten dar[587] (s = 4, r = 6, z = 6), der ersten entspricht z.B. eine Mainbrücke in Frankfurt [42], II, 5, S. 264, der letzten die Viaurbrücke der Eisenbahn Carmaux-Rodez in Frankreich mit dem größten Bogen (220 m) in Europa [32], [42], II, 5, S. 417. Die Trägerart Fig. 29 ist dreifach statisch unbestimmt (s = 1, r = 6, vgl. [36], II, 1, S. 402), würde jedoch wie bei der Mirabeaubrücke in Paris [29] in der Mitte ein Gelenk eingeschaltet, so hätte man eine zweifach statisch unbestimmte Trägerart. Vgl. a. [26]. Andre Fälle s. Bogen, durchlaufende, Bd. 2, S. 153, und Hängebrücken, feste, Bd. 4, S. 726. Einige Beispiele des selteneren Falles, daß mehr als zwei Scheiben an einer Stelle zusammenstoßen, sind in Fig. 30–32 angedeutet. Alle drei Trägerarten sind stabil, dagegen Fig. 30 und 31 einfach statisch unbestimmt (s = 3, r = 7, s = 3 bezw. s = 4, r = 7, z = 6, vgl. Sprengwerke, S. 227), Fig. 32 statisch bestimmt (s = 4, r = 6, z = 6).

Ein Trägersystem heißt statisch bestimmt oder statisch unbestimmt, je nachdem bei bekannt gedachten äußeren Kräften der Scheiben (Aktivkräfte, Stützenreaktionen, Zwischenreaktionen) die mit ihnen ins Gleichgewicht tretenden Resultanten der inneren Kräfte (z.B. die Stabkräfte eines Fachwerks) durch die Statik allein bestimmt sind oder nicht. Es heißt stabil oder labil, je nachdem, abgesehen von elastischen Formänderungen, die Scheiben in sich unverschiebbar oder mit den äußeren Kräften veränderlich sind. Demnach kann bei einem Träger die Art statisch bestimmt oder stabil, das System aber statisch unbestimmt oder labil sein und umgekehrt. Fig. 2 beispielsweise zeigt einen Träger von statisch bestimmter Art, während bei Herstellung mit voller Wand oder Gitterwerk das System statisch unbestimmt wäre. Träger von statisch bestimmter oder stabiler Art heißen auch äußerlich statisch bestimmte bezw. äußerlich stabile Träger, Träger von statisch bestimmtem oder stabilem System innerlich statisch bestimmte bezw. innerlich labile Träger. Damit ein Träger ohne Einschränkung statisch bestimmt stabil sei, muß sowohl seine Art wie sein System statisch bestimmt und stabil sein, womit der ganze Träger innerhalb der üblichen Beanspruchungsgrenzen nur durch elastische Formänderungen und Temperaturänderungen bedingte Verschiebungen erleidet und alle äußeren und inneren Kräfte durch die Gesetze der Statik allein bestimmt werden können. Vgl. Fachwerk, Bd. 3, S. 535.

Bezüglich der Anordnung und Berechnung der wichtigsten Träger sind Angaben und Literatur unter besonderen Stichworten zu finden. S. Parallelträger, Dreiecksträger, Polonceauträger, Trapezträger, Parabelträger, Halbparabelträger, Ellipsenträger, Schwedlerträger, Paulische Träger, Balken und Bogen (auch einfache und durchlaufende, Bd. 1, S. 507, 518, Bd. 2, S. 153, 155), Gelenkträger, Ketten, Gewölbe, Blechträger, Gitterträger, Fachwerke (auch statisch bestimmte, statisch unbestimmte und mehrfachen Systems, Bd. 3, S. 543, 548, 551), Balkenfachwerke, Bogenfachwerke, Hängebrücken (auch feste, Bd. 4, S. 726), Träger, zusammengesetzte (kombinierte), Bogen mit Zugstange, Bogensehnenträger, Mittengelenkbalken, Hängewerke, Sprengwerke, eventuell auch Auflager, Einspannung, Belastung der Träger, Eigengewicht, Verkehrslast, Winddruck, Lastäquivalente, Angriffsmoment, Schnittkräfte, Schnittmomente, Körper von gleichem Widerstande, Einflußlinien, Grenzwerte, Verschiebungsarbeit, Elastische Linie, Einsenkungen, Biegung, Gegenseitigkeit der Verschiebungen, Knickfestigkeit, Gegendiagonalen, Nebenspannungen, Nietverbindungen, Dimensionenberechnung, Zulässige Beanspruchungen, Spannweite u.s.w. Es empfiehlt sich im allgemeinen, zunächst das speziellste der einschlagenden Stichworte aufzusuchen.

Literatur: [1] Köpeke, Ueber den Bau eiserner Brücken, Zeitschr. d. Arch.- u. Ingen.-Vereins zu Hannover 1865, S. 71 (s.a. 1865, S. 346; 1861, S. 231; 1880, S. 112; 1888, S. 30, 373; 1889, S. 167). – [2] Heinzerling, Die Brücken in Eisen, Leipzig 1870. – [3] Weyrauch, Allgemeine Theorie und Berechnung der kontinuierlichen und einfachen Träger, Leipzig 1873. – [4] Foeppl, Vorschläge für die Konstruktion eiserner Bogenbrücken, Deutsche Bauztg. 1875, S. 91. – [5] Ržiha, Eisenbahnunter- und -oberbau, II, Wien 1877, S. 125, 141, 211, 455. – [6] Foeppl, Die neuen Trägersysteme für eiserne Brücken, Leipzig 1878. – [7] Ders., Der Träger mit sechs Gelenken, Zivilingenieur 1879, S. 197. – [8] Ders., Theorie des Fachwerks, Leipzig 1880. – [9] Weyrauch, Kennzeichen statisch bestimmter und stabiler Trägerarten, Zeitschr. f. Baukunde 1881, S. 55. – [10] Winkler, Theorie der Brücken, I, Wien 1886, S. 17; II, Wien 1881, S. 216, 218 u.s.w. – [11] Land, Ueber die statische und geometrische Bestimmtheit der Träger, insbesondere der Fachwerkträger, Zentralbl. der Bauverw. 1887, S. 363. – [12] Weyrauch, Theorie der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1887. – [13] Ders., Beispiele und Aufgaben zur Berechnung der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1888. – [14] Land, Kinematische Theorie der statisch bestimmten Träger, Zeitschr. d. Oesterr. Arch.- u.[588] Ingen.-Ver. 1888, S. 11, 162. – [15] Ritter, Anwendungen der graphischen Statik, I–IV, Zürich 1888–1906. – [16] Häseler, Der Brückenbau, I, Die eisernen Brücken, Braunschweig 1888–1908. – [17] Lang, Zur Entwicklungsgeschichte der Spannwerke des Bauwesens, Riga 1890. – [18] Hübner, Durchgehende Träger mit Querkraftnullfeldern, Zeitschr. f. Bauw. 1891, S. 549. – [19] Foeppl, Das Fachwerk im Räume, Leipzig 1892. – [20] Müller-Breslau, Beitrag zur Theorie des räumlichen Fachwerks, Zentralbl. d. Bauverw. 1892, S. 201, 225, 244, 256. – [21] Seefehlner, Beiträge zu den bei eisernen Balkenbrücken vorkommenden Berechnungen, Allg. Bauztg. 1893, S. 25, 33, 49, 57, 73, 83. – [22] Zschetzsche, Theorie lastverteilender Querverbände, Zeitschr. d. Oesterr. Ingen.- u. Arch.-Ver 1893, S. 553, 573, 588, 607. – [23] Labes bezw. Thuillé, Zur Anwendung verzahnter und verdübelter Träger, Zentralbl. d. Bauverw. 1895, S. 197 bezw. 296 (s.a. Wochenschr. d. Oesterr. Ingen.- u. Arch.-Ver. 1891, S, 21, 30, 46, 174, 203, 279, 299, 328, 349, 357; 1892, S. 405, 557; Zeitschr. d. Ver. deutsch. Ingen. 1892, S. 100, 639). – [24] Hauger, Belastung und Berechnung eiserner Brücken, Allg. Bauztg. 1896, S. 110. – [25] v. Leibbrand, Gewölbte Brücken, Leipzig 1897. – [26] Melan, Bogenträger mit vermindertem Horizontalschub, Oesterr. Monatsschrift s.d. öffentl. Baudienst 1897, 7. Heft. – [27] Weyrauch, Die elastischen Bogenträger, ihre Theorie und Berechnung entsprechend den Bedürfnissen der Praxis, München 1897 (neue Auflage in Vorbereitung). – [28] Müller-Breslau, Ueber die Berechnung statisch unbestimmter Auslegerbrücken, Zentralbl. d. Bauverw. 1897, S. 501, 513. – [29] Die Mirabeaubrücke in Paris, ebend. 1897, S. 241, 257. – [30] Bohny, Der Eingelenkbogen, Zeitschr. f. Arch. u. Ingenieurwesen 1898, S. 147. – [31] Müller-Breslau, Beitrag zur Theorie der Kuppel- und Turmdächer und verwandter Konstruktionen, Zeitschr. d. Ver. deutsch. Ingen. 1898, S. 1205, 1233. – [32] Théry, Notes sur la construction du viaduc du Viaur, Ann. des ponts et chaussées 1898, I, S. 215, und II, S. 329; 1899, I, S. 57, und IV, S. 79; 1901, III, S. 244. – [33] Landsberg, Die Statik der Hochbaukonstruktionen, Stuttgart 1899 (aus dem Handbuch der Architektur). – [34] Mehrtens, Der deutsche Brückenbau im 19. Jahrh., Berlin 1901 (auch Zeitschr. d. Ver. deutsch. Ingen. 1900). – [35] Weyrauch, Ueber die Zunahme der Brückenspannweiten im 19. Jahrhundert, Zeitschr. f. Bauwesen 1901, S. 465, 617. – [36] Müller-Breslau, Die graphische Statik der Baukonstruktionen, I–II, Leipzig 1901/08. – [37] Zimmermann, Ueber Raumfachwerke, Berlin 1901. – [38] Barkhausen, Die Balkendecken, Stuttgart 1901. – [39] Foerster, Die Eisenkonstruktionen der Ingenieurhochbauten, Leipzig 1903. – [40] Mehrtens, Vorlesungen über Statik der Baukonstruktionen und Festigkeitslehre, I–III, Leipzig 1903/05. – [41] Freitag, Gesetzmäßigkeiten in der Trägertheorie, Berlin 1904 (Dissertation). – [42] Handbuch der Ingenieurwissenschaften, II, Der Brückenbau, Leipzig, 1. Die Brücken im allgemeinen, steinerne Brücken, 1904; 2. Die eisernen Brücken im allgemeinen, Theorie der eisernen Balkenbrücken, 1901; 3. Die Konstruktion der eisernen Balkenbrücken, 1907; 4. Bewegliche Brücken, 1907; 5. Eiserne Bogenbrücken und Hängebrücken, 1906; 6. Eiserne Brückenpfeiler 1903. – [43] Schütz, Beiträge zur Bewegungslehre der ebenen statisch bestimmten Fachwerkträger, Zeitschr. f. Aren. u. Ingenieurwesen 1905, S. 154. – [44] Bohny, Theorie und Konstruktion versteifter Hängebrücken, Leipzig 1905. – [45] Mohr, Abhandlungen aus dem Gebiete der technischen Mechanik, Berlin 1906. – [46] Schlink, Statik der Raumfachwerke, Leipzig und Berlin 1907. – [47] Foerster, Das Material und die statische Berechnung der Eisenbetonbauten, Leipzig 1907. – [48] Mörsch, Der Eisenbetonbau, seine Theorie und Anwendung, Stuttgart 1908. – [49] v. Emperger, Handbuch für Eisenbetonbau, I, Berlin 1908. – [50] Haberkalt und Postuvanschitz, Die Berechnung der Tragwerke aus Betoneisen oder Stampfbeton bei Hochbauten und Straßenbrücken, Wien 1908. – S.a. die Literatur unter den oben im letzten Absatze erwähnten Stichworten.

Weyrauch.

Fig. 1.

Fig. 3.

Fig. 2., Fig. 4., Fig. 5.

Fig. 6., Fig. 7.

Fig. 8., Fig. 9., Fig. 10., Fig. 11.

Fig. 12., Fig. 13., Fig. 14.

Fig. 15., Fig. 16., Fig. 17.

Fig. 18.

Fig. 19., Fig. 20., Fig. 21.

Fig. 22., Fig. 23.

Fig. 24., Fig. 25., Fig. 26.

Fig. 27.

Fig. 28., Fig. 29.

Fig. 30., Fig. 31., Fig. 32.