Online-Bibliothek

Gelenk

[355] Gelenk. Zwei Körper, die beweglich, insbesondere drehbar, miteinander verbunden sind, bilden ein Gelenk. Die beiden Körper heißen die Glieder des Gelenkes.

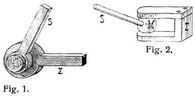
Sind die beiden Glieder S, Σ in Fig. 1 derart verbunden, daß sich ein Vollzylinder des Gliedes S in dem entsprechenden Hohlzylinder des Gliedes Σ dreht, oder werden diese [355] Zylinderflächen allgemeiner durch koaxiale Rotationsflächen ersetzt, dann bilden diese beiden Glieder ein Achsengelenk. Sind in Fig. 2 die beiden Glieder S, Σ derart verbunden, daß eine Kugel des Gliedes S in zwei entsprechenden kleinen konzentrischen Kugelhauben oder in einer diese Kugel genügend umfassenden Kugelhaube das Glied Σ berührt, dann bilden die beiden Glieder ein Kugelgelenk. Im weiteren Sinne kann auch ein Gelenk durch drei Körper gebildet werden, von denen zwei derselben durch den dritten beweglich verbunden sind, wie z.B. bei dem

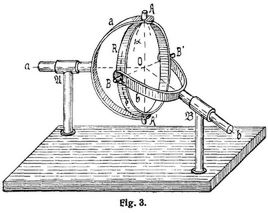
Cardanischen Gelenk. In Fig. 3 ist in der am meisten vorkommenden Gestaltung ein Cardanisches Gelenk dargestellt. An einem Ring R sind in rechtwinkligen Durchmessern die vier Zapfen A A' B B' beteiligt, so daß A A' und B B' zwei rechtwinklige Achsen bilden. Die Achse A A' ist in dem Bügel a gelagert, der sich mit der im festen Lager A befindlichen Welle dreht; die Achse B B' ist in dem Bügel b gelagert, der sich mit der im festen Lager B befindlichen Welle dreht, und die Wellenachsen a, b schneiden sich in dem Mittelpunkt O des Ringes R. Wenn die eine Welle gleichförmig gedreht wird, so dreht sich durch diese gelenkige Verbindung auch die andre Welle, aber nicht gleichförmig, und es wird demnach durch das Cardanische Gelenk bei zwei sich schneidenden Wellenachsen eine Drehung von einer Welle auf eine andre übertragen. Werden die Achsen A A', B B' in der Kreuzform A A' B B' als Zwischenglied hergestellt, so wird durch dieses Glied der Ring R ersetzt und kann weggelassen werden. In theoretischer Hinsicht gestaltet sich das Cardanische Gelenk einfacher, wenn wir das kreuzförmige Glied durch ein winkelförmiges Glied A O B oder durch das Viertelstück A B des Ringes R ersetzen und von jedem Bügel nur den einen Arm verwenden, in dem bezw. die Achsen A O, O B gelagert sind.

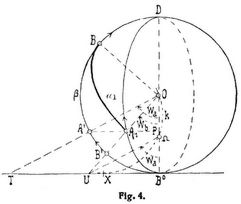
Um den Drehungsvorgang der Wellen zu veranschaulichen, denken wir uns um den Punkt O als Mittelpunkt eine Kugelfläche, welche die Achsen O A, O B in den Punkten A, B schneidet; dann bewegen sich die durch den Viertelbogen A B eines größten Kugelkreises verbundenen Punkte A, B bezw. auf den größten Kugelkreisen α, β, deren Ebenen bezw. auf den Wellenachsen a, b senkrecht sind. Ist in Fig. 4 der größte Kugelkreis β, auf dem sich der Punkt B bewegt, in wahrer Größe, und der größte Kugelkreis α, auf dem sich der Punkt A bewegt, durch eine Ellipse α₁ in senkrechter Projektion dargestellt, dann wird die im Kugelmittelpunkt O auf O B senkrechte Ebene durch eine Gerade O U dargestellt, die einerseits die Ellipse α₁ im Punkt A₁ und den Kreis β im Punkt B' schneidet; und dieser Punkt B' bewegt sich auf dem Kreise β ebenso wie der Punkt B, weil der Bogen A B oder der Winkel A₁ O B = 90° konstant ist. Denken wir uns den Kreis α um den Durchmesser B⁰ D gedreht, so daß derselbe mit dem Kreise β zusammenfällt, und ziehen wir A₁ A' senkrecht zu B⁰ D, dann gelangt der Punkt A, dessen Projektion A₁ ist, nach A'. Rotiert also der Punkt B' von B⁰ ausgehend auf dem Kreise β, wird demnach die Welle b, die auf der Ebene des Kreises β senkrecht ist, um den Winkel B⁰ O B' = w_b gedreht, so dreht sich die Welle a, die auf der Ebene des Kreises β senkrecht ist, um einen Winkel von der Größe B⁰ O A' – w_a. Bezeichnet c den Winkel, den die Wellenachsen einschließen, oder den gleichen Winkel, den die Kreisebene α mit der Kreisebene β bildet, und ist P der Fußpunkt der auf B⁰ D Senkrechten A' A₁ so ergibt sich: cos c = A₁ P : A' P. Bezeichnen T, U die Schnittpunkte, welche die Geraden O A', O B' mit der auf B⁰ D Senkrechten B⁰ T bilden; ziehen wir zu T O die Parallele U Ω, bis an B⁰ D, dann ist der Winkel B⁰ Ω U = w_a, und

Ω B⁰/O B⁰ = U B⁰/T B⁰ = A₁ P/A' P = cos c.

Wird auf O B⁰ der Punkt Ω so bestimmt, daß Ω B⁰ : O B⁰= cos c ist, dann entspricht einem Drehungswinkel B⁰ Ω U = w_a der Welle et der Drehungswinkel B⁰ O U = w_b der Welle b, und umgekehrt. Konstruieren wir den Kreis k, der durch die Punkte O Ω geht und die Gerade B⁰ T in einem Punkt X berührt, dann ergeben sich durch O X, Ω X die Drehungswinkel B⁰ O X, B⁰ Ω X, bei denen die Winkeldifferenz w_a – w_b am größten ist; und der Symmetrie entsprechend treten vier solche Lagen während einer Umdrehung der Wellen auf. Durch diese graphische Beziehung wird der Drehungsvorgang der beiden Wellen am einfachsten veranschaulicht. Ferner ergibt sich, weil tg w_a = B⁰ U/Ω B⁰, tg w_b = B⁰ U/O B⁰, cos c = Ω B⁰/O B⁰ ist, die Gleichung tg w_b/tg w_a = cos c.

Wenn die eine Welle sich gleichförmig dreht, so vergrößert sich hiernach die Ungleichförmigkeit[356] der Drehung der andern Welle mit der Vergrößerung des konstanten Winkels c bis 90°, und beide Drehungen sind nur dann gleich, wenn c = o, die Wellenachsen also in einer Geraden liegen. Die Vergrößerung des Winkels c ist aber durch die praktische Ausführung und Verwendung beschränkt und kann in der Regel 30° nicht überschreiten. – Um das veränderliche Verhältnis der Drehgeschwindigkeiten v_a, v_b der beiden Wellen 0,6 zu erhalten, differenzieren wir jene Gleichung, und es ergibt sich

Demnach ist

Dieses Verhältnis erreicht für sin w_a = ± 1 seinen größten Wert 1 : cos c und für w_a = o seinen kleinsten Wert cos c [1].

Betrachten wir in Fig. 3 das Bügelglied bb als fest, das Bügelglied a a aus dem Lager A genommen und als frei herabhängend, dann erhalten wir die sogenannte Cardanische Aufhängung (vgl. Aufhängung, Bd. 1, S. 352), der man diesen Namen mit Unrecht gegeben hat, denn Cardano [2] selbst erwähnt diese Aufhängung als eine alte bekannte Vorrichtung. Diese Aufhängung befindet sich in dem Album von Villard de Honnecourt [3] aus dem 13. Jahrhundert; und Berthelot [4] erwähnt das Vorkommen derselben in einer Handschrift »Mappae clavicula« aus dem 12. Jahrhundert. Nach der Cardanischen Aufhängung ist das Cardanische Gelenk benannt, das auch Cardanische Kupplung heißt. Ferner sind hierfür auch die Benennungen Universalgelenk, Hooksches Gelenk und Hookscher Schlüssel gebräuchlich.

Literatur: [1] Weisbach-Herrmann, Ingenieur- und Maschinenmechanik, Braunschweig 1876, 3. Teil, Abt. 1, S. 146; Grashof, Theoretische Maschinenlehre, Bd. 2, S. 157, Leipzig 1883. – [2] Cardanus, De subtilitate, Lugduni 1554; Lib. XVII, De artibus artificiosisque rebus, S. 611. – [3] Lassus, J.B. A., Album de Villard de Honnecourt, Paris 1858, S. 10, Blatt 16. – [4] Comptes rendus de l'Académie, Paris 1890, Heft 11, S. 940.

Burmester.

Fig. 1., Fig. 2.

Fig. 3.

Fig. 4.