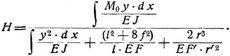Versteifungsbalken
[785] Versteifungsbalken (Versteifungsträger), ein mit schlaffen oder gering steifen Hänge- oder Stützträgern so in Verbindung gebrachter gerader Balkenträger, daß erstere unter wechselnder Belastung nur solche Formänderungen annehmen können, die den elastischen Durchbiegungen des Versteifungsträgers entsprechen.
Die Versteifungsträger spielen insbesondere bei jenem System der Hängebrücken, bei welchem das Hängewerk in sich selbst nicht steif ist (Kabel, Stabkette), eine wichtige Rolle (s. Hängebrücken). Aber auch das System der Stützträger mit Versteifungsbalken findet praktische Anwendung in der Form der hölzernen Sprengwerke, ferner bei Bogenträgern, bei welchen der Bogen als Stabpolygon mit Gelenkknoten oder wenigstens mit kleinem für die Aufnahme der Biegungsmomente ungenügendem Querschnittsträgheitsmomente ausgeführt ist (s. Bogenbrücken).
Melan.
Zur statischen Berechnung solcher Bauwerke verwendet man am besten Einflußflächen (s.d.).
Bei irgend einer Belastung P des Versteifungsträgers entsteht im Seil A' B' sowie in den beiden Rückhaltseilen eine Zugkraft, deren horizontale Komponente in allen drei Teilen gleich H ist, da über A' und B' reibungslose Rollenlager vorausgesetzt werden. Das Gesetz der virtuellen Verschiebungen, angewendet auf den Belastungszustand H = 1 mit unbelastetem Versteifungsträger und den tatsächlichen Verschiebungszustand bei P und H, ergibt
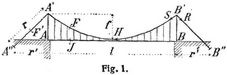
M' ist das Moment an der Stelle x des Versteifungsträgers im Zustand H = 1, und ist, da das Seil als Seilpolygon für die in diesem Zustand auf den Versteifungsträger wirkenden Kräfte gelten kann, gleich – 1 y (Fig. 2). Das im tatsächlichen Belastungszustand P vorhandene Biegungsmoment des Versteifungsträgers ist M = M0 – H y. Das ∫ S' S d s bezieht sich auf das Tragseil und die beiden Rückhaltseile. Für das Tragseil ist S = H d s/d x, S' = 1 d s/d x, somit
Für die Parabel ist genau genug d s : d x = 1 + 32 f2 x2/l4 und
somit
Für die zwei Rückhaltkabel ist
Wir erhalten also aus Gleichung 1:
Unter der Voraussetzung der[785] Parabelform für das Tragseil ist
Nach der Theorie der virtuellen Arbeiten ist
wo δ' die Hebung des Angriffspunktes der Last P im Zustand H = 1 bedeutet. (Verschiebungszustand H = 1 und Belastungszustand P, M0, H = 0.) Graphisch läßt sich also die Einflußlinie von H als Biegungslinie des Versteifungsträgers für den Zustand H = 1 ermitteln. Zu diesem Zweck fassen wir die Kurve A' B' als das Seilpolygon für die in den Hängestangen auf den Versteifungsträger wirkenden Kräfte und die Fläche zwischen ihr und der Sehne A' B' als die entsprechende Momentenfläche dieses Trägers auf. Man teilt dann den Balken in eine Anzahl Elemente von der Länge ∆ x, berechnet für jedes Element den Formänderungswinkel (s.d.) ∆ δ = M' · ∆ x : E J = 1 · y · ∆ x : E J und bildet damit ein Kräftepolygon (Fig. 2, links). Das Trägheitsmoment J des Balkenquerschnitts ist bei Fachwerken gleich 1/2 F h2 zu setzen, wo F den Gurtquerschnitt und h die Fachwerkshöhe bezeichnet. Bei Parallelträgern darf J als konstant angesehen werden; dann kann man die Berechnung der ∆ δ umgehen und braucht an deren Stelle bloß die y oder einen Bruchteil davon als Kräfte aufzutragen. Meißens ist die Kurve A' B' eine Parabel; dann wird y = f – (4 f x2 : l2) und
Es ist also P δ' = P · h · z (Fig. 2), und man erhält
Macht man, wie es in Fig. 2. geschehen ist,
und setzt
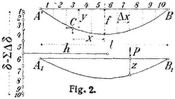
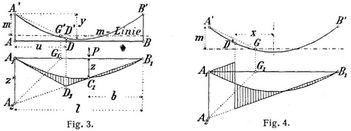
so wird H = P · z : m (vgl. Bogen mit zwei Gelenken, Bd. 2, S. 145). Die Länge m wird am einfachsten durch Rechnung bestimmt. Die Elastizitätsmaße E können für Balken und Seil verschieden eingesetzt werden. Man kann also die Linie A1 B1 als Einflußlinie von H betrachten, wenn man die Größe m als Einheit des Ordinatenmaßstabes wählt. Um nun die Einflußfläche für das Biegungsmoment im Punkt D zu erhalten, bildet man nach der Gleichung M = M0 – H y die Differenz der Einflußfläche von H y und M0. Erstere wird durch die Kurve A1 C1 B1 (Fig. 3), letztere durch das Dreieck A1 D1 B1 dargestellt. Um den Punkt D1 zu finden, zieht man im Abstande m von A' B' die m-Linie, verbindet den über D liegenden Seilpunkt D' mit A', lotet den Schnittpunkt G hinunter nach G1 zieht G1 A2 unter 45° und verbindet A2 mit B1. Denn legt man lotrecht über dem Nullpunkt C1 der Einflußfläche eine Last P auf, so ist der Horizontalzug H = P z : m, der lotrechte linke Auflagerdruck A = P b : l, folglich das Biegungsmoment in D gleich H y – A u = P (z y : m – b u : l). Da aber in der Zeichnung y : m = u : z' und z' : z = l : b ist, so wird das Biegungsmoment in D Null. – Soll die Einflußfläche für die Querkraft in D bestimmt werden (Fig. 4), so zieht man A' G parallel zur Tangente in D' und verfährt wie oben, denn es ist Q = Q0 – H tg α. Die Ordinaten der Einflußlinien sind noch mit tg α zu multiplizieren und m ist als Einheit des Maßstabes zu betrachten. Durch Anwendung des Gesetzes der virtuellen Arbeiten für den Belastungszustand H = 1 und den tatsächlichen Spannungszustand bei einer Temperaturänderung t findet man den Horizontalschub infolge einer Temperaturänderung t : Ht = 3 α t E J/2 f l2 m (l2 + 16/3 f2 + 2 r2 l/r').
Im allgemeinen verfährt man nun bei der Berechnung einer versteiften Hängebrücke wie folgt: Zuerst berechnet man den Horizontalzug Hg für Eigengewicht. Wäre das Seil unelastisch (F = F = ∞), so ergäbe sich H' g = g l2 : 8 f und m' = 4/5 f. Infolge der Elastizität des Seiles verhält sich aber Hg : H' g = m' : m, folglich ist Hg = g l2 : 10 m. In gleicher Weise wird der Horizontalzug für volle Verkehrslast Hp = p l2 10 m. Nun ist der größte Horizontalzug des Seiles = Hg + Hg + Ht, der kleinste = Hg – Ht. Die Seilspannung an einer beliebigen Stelle ist
diejenige an den Auflagern
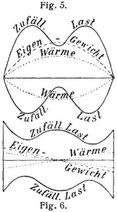
die Spannung im Rückhaltseil R = H r : r'. Der Versteifungsbalken hat vom Eigengewicht ein parabolisch verlaufendes Biegungsmoment aufzunehmen, welches in der Mitte Mg = 1/8 g l2 – Hg f ist. Die Biegungsmomente der zufälligen Last benimmt man mittels der Einflußflächen (Fig. 3), wobei man die Produkte aus Lauen und Einflußordinaten noch mit y zu multiplizieren hat und m als Einheit des Ordinatenmaßstabes benutzen muß. Die Wärmeschwankung führt ebenfalls zu einer parabolischen Momentenfläche;[786] ihr Scheitelwert ist Mt = Htf. Was die Querkräfte betrifft, so liefert das Eigengewicht eine gerade Linie mit dem Endwerte Qg = 1/2 g l – (4 Hg f : l). Die Querkräfte der zufälligen Last werden mittels der Einflußflächen (Fig. 4) bestimmt, und zwar wird Qp = 8 P f x Σ (z) : l2 m, denn tg α = 8 f x : l2. Die Querkraft für die Wärmeänderung wird wieder durch eine Gerade mit dem Endwerte Qt = 4 Ht f : l dargestellt. Fig. 5 Stellt die Kurven der Biegungsmomente für einen bestimmten Fall dar, Fig. 6 die Kurven der Querkräfte.
Das abgeleitete Verfahren kann auch auf Bogenträger mit Versteifungsbalken angewendet werden, sobald das Trägheitsmoment des Bogens viel kleiner als das des Balkens ist.
Vgl. a. Hängebrücken und Träger, zusammengesetzte.
Literatur: Ritter, Schweizerische Bauztg. 1883, S. 6 ff.; Müller-Breslau, Graphische Statik der Baukonstruktionen, Bd. 2, Leipzig 1892.
Mörsch.
Buchempfehlung
Anonym
Schi-King. Das kanonische Liederbuch der Chinesen
Das kanonische Liederbuch der Chinesen entstand in seiner heutigen Textfassung in der Zeit zwischen dem 10. und dem 7. Jahrhundert v. Chr. Diese Ausgabe folgt der Übersetzung von Victor von Strauß.
298 Seiten, 15.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Geschichten aus dem Sturm und Drang. Sechs Erzählungen
Zwischen 1765 und 1785 geht ein Ruck durch die deutsche Literatur. Sehr junge Autoren lehnen sich auf gegen den belehrenden Charakter der - die damalige Geisteskultur beherrschenden - Aufklärung. Mit Fantasie und Gemütskraft stürmen und drängen sie gegen die Moralvorstellungen des Feudalsystems, setzen Gefühl vor Verstand und fordern die Selbstständigkeit des Originalgenies. Michael Holzinger hat sechs eindrucksvolle Erzählungen von wütenden, jungen Männern des 18. Jahrhunderts ausgewählt.
- Jakob Michael Reinhold Lenz Zerbin oder Die neuere Philosophie
- Johann Karl Wezel Silvans Bibliothek oder die gelehrten Abenteuer
- Karl Philipp Moritz Andreas Hartknopf. Eine Allegorie
- Friedrich Schiller Der Geisterseher
- Johann Wolfgang Goethe Die Leiden des jungen Werther
- Friedrich Maximilian Klinger Fausts Leben, Taten und Höllenfahrt
468 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum