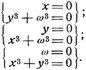Kurven
[13] Kurven, krumme Linien, stetige Reihen von Punkten in der Ebene. Eine solche wird durch eine Gleichung zwischen zwei Veränderlichen f (x, y) = 0 oder homogen f (x, y, ω) = 0, aufgelöst y = φ (x) dargestellt. Je nach der Natur der Funktion f (oder φ) heißt die Kurve algebraisch oder transzendent. Uebrigens können die Veränderlichen auch als Funktionen eines Parameters gegeben sein: x = φ (t); y = ψ (t).
A. Projektivische Eigenschaften der algebraischen Kurven. Der Grad n der Kurvengleichung in x, y heißt Ordnung; er ist die Zahl der Schnittpunkte der Kurve mit einer beliebigen Geraden. Zwei Kurven von den Ordnungen m und n haben m n Punkte gemein. Eine Kurve n-Ordnung ist im allgemeinen durch n(n + 3) : 2 Punkte bestimmt.
Die gerade Verbindungslinie zweier aufeinander folgenden Punkte der Kurve heißt Tangente. Die Gleichung der Tangente im Punkt (x y ω) ist ξ ∂f/∂x + η ∂f/∂y + ∂f/∂ω = 0 (ξ, η laufende Koordinaten). Die Tangente in einem unendlich fernen Punkt der Kurve heißt Asymptote. Setzt man die höchsten Glieder der Kurvengleichung Null, so erhält man n Gerade durch den Ursprung parallel zu den n Asymptoten. y = λ x eine derselben, so setzt man y = λ x + c in die Kurvengleichung ein. Aus der erhaltenen Gleichung bestimmt man c durch Nullsetzen des höchsten Koeffizienten von x, dann ist y = λ x + c Asymptote. Die unendlich vielen Tangenten können ebenso zur Bestimmung der Kurve dienen wie die Punkte; dieselbe wird dann als Strahlenkurve aufgefaßt. Die Koordinaten einer Tangente sind u : v : 1 = ∂ f/∂ x : ∂ f/∂ y : ∂ f/∂ ω; hieraus und durch Elimination von x : y : ω aus der Kurvengleichung f (x, y, ω) = 0 ergibt sich die Gleichung der Kurve in Linienkoordinaten. Der Grad dieser Gleichung, d.h. die Zahl n (n – 1) heißt Klasse der Kurve; sie ist die Zahl der von einem beliebigen Punkte (ξ, η) an die Kurve gehenden Tangenten. Durch deren Berührungspunkte geht eine Kurve (n – 1)-Ordnung hindurch, die erste Polare des Punktes (ξ, η) in bezug auf die Kurve ξ ∂ f/∂ x + η ∂ f/∂ y + ∂ f/∂ ω= 0. Die Berührungspunkte der Tangenten von (ξ, η) an diese Kurve liegen auf der zweiten Polaren ξ2 ∂2 f/∂ x2 + 2 ξ η ∂2 f/∂ x ∂ y + ... + ∂2 f/∂ ω2 = 0 u.s.w. Die r-Polare eines Punktes in bezug auf seine s-Polare ist die (r + s) Polare des Punktes in bezug auf die Grundkurve. Liegt (x, y) auf der r-Polare von (ξ, η), so liegt (ξ, η) auf der (n – r)-Polare von (x, y).
Ein Punkt der Kurve heißt regulär, wenn eine beliebige Gerade durch ihn einen Punkt, die Tangente aber zwei Punkte mit der Kurve gemein hat; andernfalls heißt er singulär. Ueber die Untersuchung einer Kurve in der Nähe eines singulären Punktes s. Parallelogramm, Newtonsches. Elementare singuläre Punkte sind: Doppelpunkte, d.h. Kurvenpunkte mit zwei verschiedenen Tangenten, und Rückkehrpunkte (Spitzen), d.h. Doppelpunkte mit zusammenfallenden Tangenten. Ihnen entsprechen als elementare singuläre Tangenten Doppeltangenten mit zwei verschiedenen Berührungspunkten und Wendetangenten, d.h. Doppeltangenten mit zusammenfallenden Berührungspunkten. Sind bezw. d, r, t, w die Zahlen der Doppelpunkte, Rückkehrpunkte, Doppeltangenten, Wendetangenten, so sind diese Zahlen mit der Ordnung n und der Klasse k verbunden durch die Plückerschen Formeln:
Als Geschlecht (Defekt) der Kurve wird die Zahl p = 1/2 (n – 1) (n – 2) – d –1 = 1/2 (k – 1) (k – 2) – t – w bezeichnet. Eine Kurve vom Geschlecht Null heißt rational. Die höheren Singularitäten entstehen durch Zusammenrücken von mehreren elementaren (Näheres s. Punkte). Der Ort der Punkte, deren (n – 2) te Polaren in Geradenpaare zerfallen, zugleich der Ort von Doppelpunkten in ersten Polaren, liegen auf der Hesseschen Kurve (s.d.) von der Ordnung 3 (n – 2). Die Mittelpunkte der zerfallenden (n – 2) ten Polaren besitzen erste Polaren mit Doppelpunkten und liegen auf der Steinerschen Kurve von der Ordnung 3 (n – 2)2. Dabei ist jedem Punkt der ersteren ein und nur ein solcher der letzteren zugeordnet, derart, daß[13] die Verbindungslinie entsprechender Punkte die Cayleysche Kurve von der Klasse 3 (n – 1) (n – 2) umhüllt.
Ist λ ein veränderlicher Parameter, so stellt f + λ φ = 0 eine unendliche Schar von Kurven, ein Kurvenbüschel durch die n2 Schnittpunkte der Kurven n-Ordnung f = 0 und φ = 0 dar. Unter den Kurven des Büschels sind 3 (n – 1)2, die Doppelpunkte besitzen, ferner m (2n + m – 3), die eine gegebene Kurve m-Ordnung berühren. Eine Kurve n-Ordnung kann erzeugt werden durch die Schnittpunkte entsprechender Kurven in je zwei projektivischen Kurvenbüscheln m ter und (n-m) ter Ordnung
ihre Gleichung ist:
Eine unendliche Doppelschar von Kurven n-Ordnung f + λ φ + μ ψ = 0 heißt Kurvennetz; im Netz sind unendlich viele Kurven mit Doppelpunkten enthalten; die letzteren liegen auf der Jacobischen Kurve von der Ordnung 3 (n – 1) (s.d.). Eine einfach unendliche Schar von Strahlenkurven heißt Kurvenschar, eine doppelt unendliche Kurvengewebe. Im Gewebe sind unendlich viele Kurven mit Doppeltangenten enthalten; letztere umhüllen die Hermitesche Kurve des Gewebes.
Eine Kurve heißt zu einer gegebenen adjungiert, wenn sie in jedem i fachen Punkt der letzteren einen (i – 1) fachen Punkt besitzt. Von diesen mehrfachen Punkten der Grundkurve abgesehen, hat dieselbe mit jeder adjungierten Kurve ein Schnittpunktsystem gemein. Ist die adjungierte Kurve von der m-Ordnung, wo m ≥ n – 2, so sind von dem Schnittpunktsystem p Punkte durch die übrigen bestimmt (p ist das Geschlecht der Grundkurve, s. oben). Zum Beispiel ist von den neun Schnittpunkten zweier Kurven dritter Ordnung einer durch die übrigen bestimmt.
Zwei Punktgruppen, die zusammen (abgesehen von den mehrfachen Punkten) ein vollständiges Schnittpunktsystem einer Kurve mit einer adjungierten Kurve bilden, heißen zueinander residual. Zwei Punktgruppen, die zur selben Punktgruppe residual sind, heißen korresidual in bezug auf letztere. Restsatz von Brill und Nöther: Sind die Gruppen Q und R in bezug auf die Gruppe Q' korresidual, so sind sie auch korresidual in bezug auf jede Gruppe R', die zu einer von ihnen residual ist. Beispiel: Gehen zwei Kegelschnitte durch vier Punkte einer Kurve dritter Ordnung und schneidet jeder die letztere noch in einem Punktepaar, so treffen sich die Verbindungsgeraden der letzteren auf der Kurve dritter Ordnung.
Liegen zwei Punktreihen auf einer und derselben Kurve n ter Ordnung als Träger, so kann zwischen denselben eine Verwandtschaft (Korrespondenz) bestehen, derart, daß jedem Punkt ξ der einen Reihe a Punkte x der andern und jedem Punkt der letzteren b Punkte ξ der ersteren entsprechen (a, b-Korrespondenz). Alsdann gilt für rationale Kurven das Chaslessche Korrespondenzprinzip: es gibt a + b Koinzidenzpunkte auf der Kurve, d.h. solche, in welchen ein Punkt § mit einem zugehörigen x zusammenfällt (Näheres s. [1], 4. Abt., 8. Abschn.)
Eine Transformation der Ebene (x, y, ω) in die Ebene (ξ, η, τ) : ρ ξ = f1 (x, y, ω); ρ η = f2 (x, y, ω); ρ τ = f3 (x, y, ω), aufgelöst: ρ x = φ1 (ξ, η, τ); σ y = φ2 (ξ, η, τ); σ ω = φ3 (ξ, η, τ), f1 f2 f3 φ1 φ2 φ3 rationale Funktionen n ter Ordnung sind, heißt eine Cremonasche Transformation, wenn jedem Punkt (x, y, ω) ein und nur ein Punkt (ξ, η, τ) entspricht. Die Kurven f1 = 0; f2 = 0; f3 = 0 haben n2 – 1 Schnittpunkte gemein, ebenso die Kurven φ1 = 0; φ2 = 0; φ3 = 0. Diese Punkte heißen Fundamentalpunkte; einem solchen entspricht nicht ein Punkt, sondern eine Kurve (Fundamentalkurve). Beispiel: die quadratische Transformation: ρ ξ = y ω; ρ η = x ω; ρ ζ = x y; σ x = η τ, σ y = ξ τ; σ ω = ξ η. Den Fundamentalpunkten
entsprechen die Geraden ξ = 0; η = 0; τ = 0. Jede Cremonasche Transformation kann durch eine Reihe aufeinander folgender quadratischer ersetzt werden. Durch Cremonasche Transformationen können höhere Singularitäten in gewöhnliche mehrfache Punkte mit verschiedenen Tangenten übergeführt werden. Eine Transformation ist keine Cremonasche, wenn die Funktionen φ1 φ2 φ3, nicht an sich rational sind, sondern es erst werden in Verbindung mit der Gleichung einer Kurve m ter Ordnung Φ (ξ, η, τ) = 0. Die Transformation ist alsdann nicht eindeutig für die beiden Ebenen, wohl aber für die Punkte der Kurve Φ (ξ, η, τ) = 0, der in der andern Ebene die Kurve Φ (f1 f2 f3) = F (x, y, ω) = 0 entspricht. Jedem Punkt von F = 0 entspricht ein und nur ein Punkt Φ = 0 (vgl. oben die Hessesche und die Steinersche Kurve). Bei einer solchen eindeutigen Ueberführung einer Kurve in eine andre bleibt das Geschlecht erhalten: jede rationale Kurve kann in eine Gerade, jede Kurve mit p = 1 in eine allgemeine Kurve dritter Ordnung übergehen.
Von den Schnittpunkten einer Kurve n ter Ordnung mit einer adjungierten Kurve (n – 3) ter Ordnung (sogenannten φ-Kurve) sind nur p – 1 durch die übrigen bestimmt. Die durch φ-Kurven ausgeschnittenen Gruppen von je Q Punkten bilden daher eine Schar (Spezialschar) von der Mannigfaltigkeit q = Q – p + 1. Riemann-Rochscher Satz: Legt man durch die q fach unendlichen Gruppen von je Q Punkten einer Spezialschar alle möglichen φ-Kurven, so schneiden diese die Grundkurve noch je in R = 2 p – 2 – Q Punkten, die eine Spezialschar von der Mannigfaltigkeit r = p – Q – q – 1 bilden. Beispiel: Aus einer Kurve fünfter Ordnung mit Doppelpunkt (p = 5) wird eine Spezialschar ausgeschnitten durch Kegelschnitte, die aus einer festen Geraden g durch den Doppelpunkt und aus einer beweglichen Geraden g1 bestehen (Q = 5, q = 2). Die drei Schnittpunkte von g mit der Kurve gehören zu einer Spezialschar, die ausgeschnitten wird durch Kegelschnitte, die in eine feste Gerade und eine bewegliche durch den Doppelpunkt zerfallen (R = 3, r = 1). Werden die Abszissen der Schnittpunkte einer Kurve mit einer adjungierten Kurve als obere Grenzen von Abelschen Integralen erster Gattung gewählt, die zu der Gleichung der Kurve gehören, so führt das Abelsche Theorem unmittelbar auf den Restsatz. Die Koordinaten der Kurvenpunkte können als Abelsche (für p = 0 als rationale, für p = 1 als elliptische, für p = 2 als hyperelliptische) Funktionen eines Parameters dargestellt werden.
B. Metrische Eigenschaften der Kurven in Parallelkoordinaten. Hierbei wird die Gleichung y = φ (x) zugrunde gelegt. Tangente im Punkt (x, y) (ξ, η laufende Koordinaten)[14] (ξ – x) φ' (x) = η – y. Normale (Lot auf der Tangente) ξ – x + (η – y) φ' (x) = 0. y' = φ' (x) ist die goniometrische Tangens des Neigungswinkels der Tangente gegen die x-Achse. Sie ist {positiv/negativ}, je nachdem die Kurve {steigt/fällt} φ'(x) = 0 gibt die Abszissen der Maxima und Minima der Kurve gegen die x-Achse; es liegt {Maximum/Minimum} vor, je nachdem (für die betreffenden x) y'' = φ'' (x) 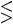 0. Ueberhaupt ist die Kurve {konkav/konvex} gegen die x-Achse, je nachdem y y''
0. Ueberhaupt ist die Kurve {konkav/konvex} gegen die x-Achse, je nachdem y y'' 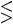 0. φ'' (x) = 0 liefert die Abszissen der Wendepunkte. Berührungsgrößen: Tangente (von Berührungspunkt bis x-Achse):
0. φ'' (x) = 0 liefert die Abszissen der Wendepunkte. Berührungsgrößen: Tangente (von Berührungspunkt bis x-Achse):
Subtangente (Projektion derselben auf die x-Achse): y/y'. Normale (bis zur x-Achse):
Subnormale (Projektion auf die x-Achse): y y'. Bogendifferential (Bogenelement zwischen zwei benachbarten Kurvenpunkten):
Kontingenzwinkel (zwischen zwei aufeinander folgenden Tangenten): d τ = y''/1 + y'2 d x. Der Schnittpunkt zweier aufeinander folgenden Normalen ist das Krümmungszentrum mit den Koordinaten x – (1 + y'2) y'/y''; y + 1 + y'2/y''. Der Kreis aus diesem Punkt durch den Kurvenpunkt (x, y) heißt Krümmungskreis und oskuliert die Kurve; sein Radius, der Krümmungsradius, ist (1 + y'2) 3/2/y''. Der Ort der Krümmungszentra heißt Evolute (s.d.). Flächeninhalt der Kurven, s. Quadratur; Bogenlänge, s. Rektifikation. Satz von Newton: Schneiden zwei Sekanten durch Punkt O (Fig. 1) eine Kurve n ter Ordnung bezw. in den Punkten R1 R2 ... Rn und S1 S2 ... Sn, so ist das Verhältnis: (OR1OR2 ... ORn)/(OS1OS2 ... OSn) nur von der Richtung der Sekanten, nicht aber von der Lage des Punktes O abhängig. Ein Punkt heißt Mittelpunkt, wenn jedem Radius O P eines Kurvenpunkts P ein gleichgroßer entgegengesetzter O P' eines Kurvenpunkts P' entspricht. Ist der Ursprung Mittelpunkt, so fehlen in der Kurvengleichung entweder die ungeraden oder die geraden Glieder; im letzteren Fall geht die Kurve durch den Mittelpunkt und hat daselbst einen Wendepunkt. Satz von Cotes: Bestimmt man in jedem von O ausgehenden Radiusvektor, der die Kurve in R1 ... Rn schneidet, einen Punkt R derart, daß
so ist der Ort von R eine Gerade, die (n – 1) te Polare von O in bezug auf die Kurve.
Zieht man in den beiden unendlich fernen imaginären Kreispunkten je die n (n – 1) Tangenten an eine Kurve n ter Ordnung, so durchschneiden sich diese in den n2 (n – 1)2 Brennpunkten der Kurve. Ist φ (u, v, w) die Gleichung der Kurve in homogenen Linienkoordinaten, so erhält man die Koordinaten der Brennpunkte, indem man in φ (1, i, – (x + i y)) = 0 den reellen und imaginären Teil für sich gleich Null setzt. Jeder Brennpunkt ist ein solcher für die Evoluten und Evolventen.
C. Metrische Eigenschaften der Kurven in Polarkoordinaten. Es sei r = ψ (ϑ) die Kurvengleichung, so ergibt sich der Winkel φ zwischen Radiusvektor und Tangente aus tg φ = r/r'; die Länge der Tangente bis zum Ursprungslot auf dem Radiusvektor
die Polarsubtangente r2/r'; Abstand der Tangente von Pol
die Normale bis zum Ursprungslot auf dem Radiusvektor
die Polarsubnormale r'. Bogendifferential
D. Kurven dritter Ordnung. Eine allgemeine Kurve dritter Ordnung hat immer einen unpaaren Zug (Serpentine) mit einer Asymptote und drei reellen Wendepunkten; sie kann noch außerdem einen paaren Zug (Oval) besitzen, der ganz im Endlichen liegt oder die unendlich ferne Gerade berührt oder zwei Asymptoten hat. Die Tangente in einem Kurvenpunkt schneidet die Kurve noch in einem weiteren Punkt, dem Tangentialpunkt des ersteren. Von einem Punkt außerhalb gehen sechs Tangenten an die Kurve, von einem Kurvenpunkt selbst noch vier. Das Doppelverhältnis derselben ist von der Lage des Kurvenpunkts unabhängig, es ist ein für die Kurve charakteristischer Modul. Durch Projektion kann jede Kurve dritter Ordnung in eine der fünf divergierenden Parabeln übergeführt werden, y2 = (x – a) (x – b)(x – c) Oval vorhanden; y2 = (x – a) (x2 + b x + c), wo b2 < 4 c Oval fehlt; y2 = (x – a)2 (x – b); a < b isolierter Punkt (a, o); y2 = (x – a)2 (x – b); a > b Doppelpunkt (a, o); y2 = (x – a)3 Rückkehrpunkt (a, o). (Denselben entsprechen fünf Mittelpunktskurven.) Die Hessesche und die Steinersche Kurve fallen zusammen; die erste Polare eines Punktes P dieser Kurve zerfällt in ein Geradenpaar, dessen Mittelpunkt Q ebenfalls auf der Kurve liegt. P und Q sind korrespondierende [15] Punkte. Die Hessesche Kurve schneidet die Grundkurve C in den neun Wendepunkten, die auch Wendepunkte der Hesseschen Kurve H sind (Fig. 2). Die Berührungspunkte der drei Tangenten von einem Wendepunkt an die Grundkurve liegen auf der harmonischen Geraden der letzteren. Die Wendepunkte, von denen drei reell sind, liegen zu je drei auf zwölf Geraden; diese bilden vier Dreiecke, von denen jedes alle Wendepunkte enthält. Auf ein Wendepunktsdreieck bezogen, lautet die Gleichung der Kurve: x3 + y3 + ω3 + 6 m x y = 0.
Die Wendepunkte sind:'
Jede Kurve dritter Ordnung ist Hessesche Kurve von drei andern Kurven dritter Ordnung. Daher können ihre Punkte auf drei verschiedene Arten als korrespondierende Punktepaare (Polpaare) angeordnet werden. Schrötersche Konstruktion der Kurve dritter Ordnung aus drei Polpaaren A A', B B', C C' vermöge des Satzes, daß sich die Verbindungslinien zweier Paare (etwa A B', A' B und A B, A' B') auf der Kurve in einem weiteren Polpaar Schneiden. Chaslessche Erzeugungsweise der Kurve dritter Ordnung als Ort der Schnittpunkte der entsprechenden Elemente eines Kegelschnittbüschels und eines dazu projektivischen Strahlenbüschels. Graßmannsche Erzeugungsweise: Ein Punkt beschreibt eine Kurve dritter Ordnung, wenn seine Verbindungslinien mit drei festen Punkten drei feste Gerade in Punkten einer beweglichen Geraden schneiden. Die Kurven dritter Ordnung mit Doppel- und Rückkehrpunkt können auf einer Geraden abgebildet werden. Zu den Kurven dritter Ordnung gehört die Cissoide und das Descartessche Blatt (Bd. 2, S. 467 und 713).
E. Kurven vierter Ordnung. Eine allgemeine Kurve vierter Ordnung ist von der zwölften Klasse und hat 24 Wendepunkte (höchstens acht reelle) und 28 Doppeltangenten, die alle reell sein können. Die Kurve kann höchstens in vier getrennte Teile zerfallen. Die Doppeltangenten sind zweierlei Art: solche, die denselben Kurventeil berühren oder isoliert sind, und solche, die verschiedene Teile der Kurve berühren.
Zu den Kurven vierter Ordnung gehören die Cartesischen Ovale (mit der Pascalschen Schnecke und der Kardioide, Fig. 3), die Cassinischen Kurven (mit der Lemniskate) und die Konchoiden.
F. Transzendente Kurven. Dieselben besitzen Singularitäten, die bei algebraischen Kurven nicht vorkommen können, z.B. Endpunkte, in welchen ein Kurvenzweig ganz aufhört, Eckpunkte, in welchen die Tangente einen endlichen Sprung macht, asymptotische Punkte, um welche die Kurve in unendlich vielen Windungen kreist u.s.w.
Transzendente Kurven sind die Cykloide, die logarithmische Kurve, die Tractrix, die Kettenlinie, die Spiralen.
Literatur: [1] Clebsch, A., Vorlesungen über Geometrie, herausg. von Lindemann, Bd. 1, Leipzig 1876, Abt. 4–6. – [2] Salmon, G., Analyt. Geometrie der höheren ebenen Kurven, deutsch von Fiedler, 2. Aufl., Leipzig 1882. – [3] Cremona, Einleitung in die geometr. Theorie der ebenen Kurven, deutsch von Curtze, Greifswald 1865. – [4] Plücker, System der analyt. Geometrie mit einer Theorie der Kurven dritter Ordnung, Berlin 1835. – [5] Ders., Theorie der algebr. Kurven, Bonn 1839. – [6] Kötter, Grundzüge einer rein geometr. Theorie der algebr. ebenen Kurven, Berlin 1887. – [7] Haas, A., Lehrb. der Differentialrechnung, 3. Teil: Anwendung der Differentialrechnung auf die ebenen Kurven, Stuttgart 1894. – [8] Reuschle, Praxis der Kurvendiskussion, Stuttgart 1886. – [9] Durège, Die ebenen Kurven dritter Ordnung, Leipzig 1871. – [10] Schröter, Theorie der ebenen Kurven dritter Ordnung, Leipzig 1888. – [11] Baur, M., Synthet. Einteilung der ebenen Linien dritter Ordnung, Stuttgart 1888. – [12] Eagles, T.H., Constructive geometry of plane curves, London 1885. – [13] Frost, P., Treatise on curve tracing, London 1872. – [14] Johnson, W.W., Curve tracing in Cartesian coordinates, New York 1885. – [15] Loria, G., Spezielle algebr. und transzendente ebene Kurven, deutsch von Schütte, Leipzig 1902. – [16] Wiener, Die Einteilung der ebenen Kurven und Kegel dritter Ordnung in 13 Gattungen, Halle 1901. – [17] Wieleitner, H., Theorie der ebenen algebr. Kurven höherer Ordnung, Leipzig 1905. – [18] Basset, A.B., An elementary treatise on cubic and quartic curves, 2. Aufl., Cambridge 1905. – [19] Ebner, F., Leitfaden der technisch wichtigsten Kurven, Leipzig 1906. – S.a. die Literatur bei Differentialrechnung.
Wölffing.
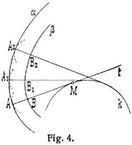
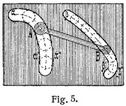
Aequidistante Kurven. Ist in Fig. 4 eine ebene Kurve k gegeben, auf der eine Tangente A t rollt, dann beschreiben die Punkte A, B, ... der Tangente äquidistante Kurven, α, β, ... Dieses Rollen der Tangente kann man sich dadurch veranschaulichen, daß man die Kurve k in der Zeichnungsebene als die Basiskurve einer senkrechten Zylinderfläche betrachtet, an der ein in A straff gehaltener seiner Faden A M, in der Zeichnungsebene bewegt, ab- oder aufgewickelt wird. Die Punkte AB ... der Tangente gelangen in die Lagen A1 B1 ..., A2 B2 ... u.s.w.; und die Tangenten A B, A1 B1, A2 B2, ... der Kurve k sind Normalen der äquidistanten Kurven α, β, ... Diese so erzeugten Kurven α, β, ... werden auch die Evolventen der Kurve k genannt[16] Die von der Normalen einer Kurve α umhüllte Kurve k heißt die Evolute der Kurve α und ist zugleich die Evolute der Kurve β. Die äquidistanten Kurven α, β, ... haben demnach dieselbe Evolute k, und der Berührungspunkt M, den die Tangente A B mit der Kurve k bildet, ist der gemeinsame Krümmungsmittelpunkt für die entsprechenden Punkte A, B, ... aller äquidistanten Kurven α, β, ... Bei äquidistanten Kurven α, β haben die entsprechenden Punkte A B, A1 B2, A2 B2, ... in den Normalen gleichen Abstand und parallele Tangenten; deshalb werden die äquidistanten Kurven auch Parallelkurven genannt. Die äquidistanten Kurven sind demnach auch solche Kurven, deren entsprechende Punkte in gemeinsamen Normalen gleichen Abstand besitzen. Beschreiben wir in Fig. 4 um die Punkte B, B1 B2, ... der Kurve β Kreisbogen, deren Radius gleich dem Abstand der äquidistanten Kurven α, β ist, so berühren diese Kreisbogen die Kurve α in den Punkten A, A1, A2, ... Wir können hiernach zu einer gegebenen Kurve β eine äquidistante Kurve α, die auch kurz eine Aequidistante der Kurve β genannt wird, punktweise erhalten, indem wir auf den Normalen der Kurve β gleiche Strecken A B, A1 B1, A2 B2, ... auftragen, oder wir können ohne diese Normalen die äquidistante Kurve α als umhüllende jener Kreisbogen zeichnen. Die äquidistanten Kurven kommen als Konturkurven bei der senkrechten Projektion der Flächen vor, welche durch Bewegung einer Kugel erzeugt werden, und finden ferner Anwendung bei der Triebstockverzahnung (s.d.) sowie bei Mechanismen mit Kurvenführung. Soll z.B. in Fig. 5 ein Glied A B eines Mechanismus auf einer Platte P so bewegt werden, daß sich zwei Gliedpunkte A, B bezw. auf gegebenen Kurven α, β bewegen, dann kann diese Bewegung durch zwei in die Platte P eingeschnittene Nuten α' α'', β' β'' und zwei in denselben gleitende zylindrische Zapfen bewirkt werden, die bezüglich A, B zentrisch an dem bewegten Gliede befestigt sind. Die Randkurven α', α'' der einen Nute werden demnach als äquidistante Kurven zu a mit den Abständen gleich dem zugehörigen Zapfenradius erhalten, und ebenso ergeben sich die Randkurven β', β'' der andern Nute als äquidistante Kurven zu β mit den Abständen gleich dem zugehörigen Zapfenradius.
Zyklische Kurven. Rollt in Fig. 6 und 7 ein Kreis p an einem festen Kreise π, dann beschreibt ein mit dem rollenden Kreise p verbundener Punkt A eine zyklische Kurve, die mit α bezeichnet ist. Bei diesem Bewegungsvorgang dreht sich die Verbindungsstrecke Φ F der Kreismittelpunkte Φ, F um den festen Kreismittelpunkt Φ, ferner dreht sich die Strecke F A in bezug auf Φ F um den bewegten Kreismittelpunkt F, und diese beiden Drehungen stehen in dem konstanten Verhältnis der Kreisradien Φ P, F P. Eine unendlich kleine Bewegung der Strecke F A in bezug auf den festen Kreis π kann angesehen werden als eine unendlich kleine Drehung um den Berührungspunkt P der Kreise p, π, und die Normale im Punkt A an der zyklischen Kurve α ist die Gerade A P. Konstruieren wir das Parallelogramm Φ F A F', dessen Seiten unveränderlich, dessen Winkel aber während der Bewegung veränderlich sind, so bewegt sich der Eckpunkt F' auf einem Kreise um Φ, und bezeichnen wir mit P' den Schnittpunkt der Geraden A P, Φ F', so kann eine unendlich kleine Bewegung der Parallelogrammseite A F' in bezug auf die feste Kreisebene als eine unendlich kleine Drehung um den Punkt P' betrachtet werden. Wegen der ähnlichen Dreiecke P F A, P Φ P' ist Φ P' = F A/F P Φ P, demnach ist die Strecke Φ P' konstant. Für alle Lagen der Parallelogrammseite A F' liegt also der Punkt P' in der festen Kreisebene auf dem um Φ mit dem Radius F' P' beschriebenen Kreise p', und ferner liegt der Punkt P' in bezug auf die bewegte Parallelogrammseite A F' auf einem um F' mit dem Radius F' P' beschriebenen Kreise p', den wir uns mit A F' verbunden denken [1]. Während der Bewegung rollt demnach der Kreis p' an dem festen Kreise π', und hieraus folgt die von Gildemeister [2] und ferner von Bellermann [3] zuerst mitgeteilte zweifache Erzeugung der zyklischen Kurve. Eine zyklische Kurve α wird erstens von dem mit dem Kreise p verbundenen Punkt A durch Rollen des Kreises p an dem festen Kreise π beschrieben und zweitens von dem mit dem Kreise p' verbundenen Punkt A durch Rollen des Kreises p' an dem festen Kreise π'. Befindet sich der beschreibende Punkt A auf der Peripherie des Kreises p, dann liegt auch der Punkt A auf der Peripherie des Kreises p' und die beiden festen konzentrischen Kreise π, π' fallen zusammen. Für diesen speziellen Fall wurde die doppelte Erzeugung zuerst von De la Hire [4] und später von Euler [5] mitgeteilt.
Die zyklischen Kurven werden Trochoiden genannt, wenn der feste und der rollende Kreis von endlicher Größe sind. Man unterscheidet Epitrochoiden und Hypotrochoiden, je nachdem der rollende Kreis, mit dem der beschreibende Punkt verbunden ist, auf dem festen Kreise oder in demselben rollt. In Fig. 6 ist demnach die zyklische Kurve α eine Epitrochoide, in Fig. 7 eine Hypotrochoide. Liegt insbesondere der beschreibende Punkt auf der Peripherie des rollenden Kreises, dann werden die zyklischen Kurven bezw. Epicykloiden oder Hypocykloiden[17] genannt. Dieselben besitzen Rückkehrpunkte oder Spitzen, die gegen den festen Kreis flößen, und heißen deshalb auch gemeinsam gespitzte Trochoiden. – Weiter unterscheidet man erstens verschlungene Trochoiden, wenn der beschreibende Punkt A und der feste Kreismittelpunkt Φ beide innerhalb oder beide außerhalb des rollenden Kreises liegen; zweitens gestreckte (auch geschweifte und gedehnte) Trochoiden, wenn sich der eine dieser Punkte innerhalb und der andre außerhalb des rollenden Kreises befindet [6], Denn wenn bei der einen Erzeugung diese beiden Punkte innerhalb des rollenden Kreises sich befinden, so liegen sie bei der andern beide außerhalb desselben; oder wenn bei der einen Erzeugung der eine innerhalb, der andre außerhalb des rollenden Kreises sich befindet, so tritt dies auch bei der andern Erzeugung ein. Die Trochoide α in Fig. 6 ist demnach eine gestreckte Epitrochoide, in Fig. 7 eine verschlungene Hypotrochoide. Rollt bei der ersten Erzeugung insbesondere ein Kreis auf einem gleichgroßen festen Kreise, so rollt bei der zweiten Erzeugung ein Kreis umschließend auf einem halb so großen festen Kreise, und die in diesen Fällen von einem Punkt beschriebene Trochoide heißt eine allgemeine Kardioide, die eine verschlungene oder gestreckte sein kann und auch Pascalsche Kurve oder Limaçon genannt wird. Befindet sich aber der beschreibende Punkt auf der Peripherie des rollenden Kreises, dann wird eine Kardioide, Herzkurve, erzeugt, die einen Rückkehrpunkt besitzt. Bei der Rollung eines Kreises in einem doppelt so großen festen Kreise werden Ellipsen und insbesondere gerade Strecken erzeugt (s. Cardanische Kreise). In Fig. 6, wo der beschreibende Punkt eine gestreckte Epitrochoide erzeugt, rollt bei der zweiten Erzeugung der Kreis p' umschließend auf dem festen Kreise π'; und man hat vor der Erkenntnis der zweifachen Erzeugung, wenn ein Kreis umschließend auf einem festen rollt, die von einem Punkt beschriebene zyklische Kurve eine »Pericykloide« genannt [7]. Diese Benennung ist also verwerflich. Ferner sind auch die noch bisher gebräuchlichen, fallen begründeten Benennungen »verlängerte« oder »verkürzte« Epicykloide oder Hypocykloide verwerflich, wenn der beschreibende Punkt innerhalb oder außerhalb des rollenden Kreises liegt. Ist der feste Kreis unendlich groß, geht derselbe also in eine Gerade über, dann beschreibt ein mit dem rollenden Kreise verbundener Punkt eine allgemeine Cykloide. Diese ist eine verschlungene Cykloide oder eine gestreckte Cykloide, je nachdem der beschreibende Punkt sich außerhalb oder innerhalb des rollenden Kreises befindet. Liegt der beschreibende Punkt auf der Peripherie des rollenden Kreises, dann wird die gemeine Cykloide oder gespitzte Cykloide erzeugt, die auch kurz Cykloide genannt wird. Ist der rollende Kreis unendlich groß, geht derselbe also in eine Gerade über, die auf dem festen Kreise rollt, dann beschreibt ein an dieser Geraden beteiligter Punkt eine allgemeine Kreisevolvente. Diese heißt eine verschlungene Kreisevolvente oder eine gestreckte Kreisevolvente, je nachdem der beschreibende Punkt auf der Berührungsseite oder auf der andern Seite der rollenden Geraden liegt. Als gemeine oder gespitzte Kreisevolvente wird sie bezeichnet, wenn der beschreibende Punkt sich auf dieser Geraden befindet. Die zyklischen Kurven kommen schon im Ptolemäischen Planetensystem vor. Ihre Erzeugung durch Rollung und Anwendung auf die Verzahnung der Räder (s.d.) soll von Desargues (1598–1662) und ferner von Olaf Römer (1674) [9] flammen.
Literatur: [1] Burmester, Lehrbuch der Kinematik, Leipzig 1888, Bd. 1, S. 134. – [2] Gildemeister, De lineis curvis epicycloidibus et hypocycloidibus, Diss., Marburg 1866. – [3] Bellermann, G., Epicyloiden und Hypocyloiden, Berlin 1867. – [4] Mémoires de l'Académie, Paris 1694, 9. Teil, S. 390. – [5] Acta Petropolitanae, Ann. 1781, 1. Teil: »De duplici genesi tam epicycloidum, quam hypocycloidum«. – [6] Vgl. Wiener, Chr., in der Zeitschr. f. Mathematik u. Physik, 1881, Bd. 26, S. 257. – [7] Weißenborn, Die cyklischen Kurven, Eisenach 1856, S. 3. – [8] Poudra, Oeuvres de Desargues, Paris 1864, 1. Teil, S. 30. – [9] Miscellanea Berolin., 1. Teil, S. 315. – Ein Modell für die gleichzeitige doppelte Erzeugung der Trochoiden wurde von L. Burmester hergestellt, s. Dyck, Katalog mathematischer Modelle, München 1892, S. 335. – Ferner wurden Modelle für die Erzeugung der cyklischen Kurven hergestellt und beschrieben von Schilling, Fr., Zeitschr. für Mathematik und Physik 1899, Bd. 44, S. 214. – Die geschichtliche Entwicklung der zyklischen Kurven wurde ausführlich behandelt von Wölffing, E., Bibliotheca mathematica 1901, 3. Folge, Bd. 2, S. 235, und von Loria, G., Spezielle algebraische und transzendente ebene Kurven, Leipzig 1902, S. 479.
Burmester.
Buchempfehlung
Jean Paul
Flegeljahre. Eine Biographie
Ein reicher Mann aus Haßlau hat sein verklausuliertes Testament mit aberwitzigen Auflagen für die Erben versehen. Mindestens eine Träne muss dem Verstorbenen nachgeweint werden, gemeinsame Wohnung soll bezogen werden und so unterschiedliche Berufe wie der des Klavierstimmers, Gärtner und Pfarrers müssen erfolgreich ausgeübt werden, bevor die Erben an den begehrten Nachlass kommen.
386 Seiten, 11.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Romantische Geschichten III. Sieben Erzählungen
Romantik! Das ist auch – aber eben nicht nur – eine Epoche. Wenn wir heute etwas romantisch finden oder nennen, schwingt darin die Sehnsucht und die Leidenschaft der jungen Autoren, die seit dem Ausklang des 18. Jahrhundert ihre Gefühlswelt gegen die von der Aufklärung geforderte Vernunft verteidigt haben. So sind vor 200 Jahren wundervolle Erzählungen entstanden. Sie handeln von der Suche nach einer verlorengegangenen Welt des Wunderbaren, sind melancholisch oder mythisch oder märchenhaft, jedenfalls aber romantisch - damals wie heute. Nach den erfolgreichen beiden ersten Bänden hat Michael Holzinger sieben weitere Meistererzählungen der Romantik zu einen dritten Band zusammengefasst.
- Ludwig Tieck Peter Lebrecht
- Friedrich de la Motte Fouqué Undine
- Ludwig Achim von Arnim Isabella von Ägypten
- Clemens Brentano Geschichte vom braven Kasperl und dem schönen Annerl
- E. T. A. Hoffmann Das Fräulein von Scuderi
- Joseph von Eichendorff Aus dem Leben eines Taugenichts
- Wilhelm Hauff Phantasien im Bremer Ratskeller
456 Seiten, 16.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum