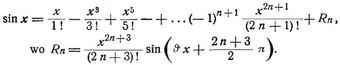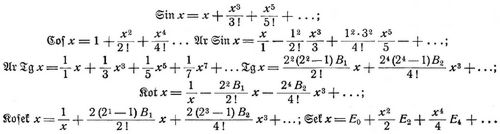Online-Bibliothek

Reihen

[397] Reihen, geordnete Folgen von mathematischen Größen (Gliedern), die nach einem gewissen Gesetz gebildet sind. Zu jedem Glied u gehört der Stellenzeiger, d.h. die Zahl, die angibt, das wievielte Glied u in der Reihe ist. Man unterscheidet Summenreihen a + b + c + ... und Produktenreihen a · b · c ..., je nachdem die Reihen Summen oder Produkte ihrer Glieder sind. Ferner teilt man die Reihen je nach der Zahl ihrer Glieder in endliche und unendliche Reihen ein. Unter den letzteren gibt es vorwärts unendliche und vor- und rückwärts unendliche, je nachdem der Stellenzeiger von 0 bis ∞ oder von –∞ über 0 nach +∞ fortschreitet. Es gibt aber auch Reihen mit mehreren Stellenzeigern (Reihen mit mehrfachem Eingang). Unter jenen mit zwei[397] Stellenzeigern werden Reihen von der Gestalt (1) als Diagonalreihen bezeichnet:

A. Endliche Summenreihen [7]. Zu denselben gehören die arithmetischen und die geometrischen Progressionen. Bei den arithmetischen Reihen (erster Ordnung) ist die Differenz zweier aufeinander folgenden Glieder konstant. Ist a das erste Glied, d die Differenz, so heißt die Reihe a, a + d, a + 2d, a + 3d ... Das n–te Glied ist a + (n – 1) d und die Summe der n ersten Glieder s = n a + ¹/₂n (n – 1) d. Ueber höhere arithmetische Reihen s. Summen und Differenzenreihen. Bei den geometrischen Progressionen ist der Quotient zweier aufeinander folgenden Glieder konstant. Ist a das erste Glied, q der Quotient, so heißt die Reihe a, a q, a q² ...; das n–te Glied ist a q^n–1 und die Summe der n ersten Glieder a(qⁿ – 1)/(q – 1). Die geometrischen Reinen spielen in der Zinseszins- und Rentenrechnung eine Rolle.

B. Unendliche Summenreihen [8]–[10]. Eine solche heißt konvergent, wenn sich die Summe S_n derselben bei wachsender Anzahl n der Glieder einem bestimmten endlichen Grenzwert S nähert. Dann kann das Restglied, d.h. die Summe der auf das n–te folgenden Glieder, durch Wahl eines hinreichend großen n beliebig klein gemacht werden. Beispiel: die Reihe 1 + ¹/₂ + ¹/₄ + ¹/₈ + ... nähert sich mit wachsender Gliederzahl dem Grenzwert 2. Nähert sich dagegen S_n mit wachsendem n keinem endlichen bestimmten Grenzwert, so heißt die Reihe divergent. Beispiel: die sogenannte harmonische Reihe 1 + ¹/₂ + ¹/₃ + ... Die Summe derselben nähert sich dem Grenzwert unendlich. Kommen in einer Reihe R Glieder mit positivem und solche mit negativem Vorzeichen vor, so kann man erstere für sich summieren, ebenso auch letztere (positiv genommen). Man erhalte bezw. R₁ und R₂, so daß R = R₁ – R₂. Sind nun R₁ und R₂ konvergent, so heißt die Reihe R absolut oder unbedingt konvergent; man kann die Reihenfolge ihrer Glieder vertauschen, ohne daß sich ihre Summe ändert. Sind dagegen R₁ und R₂ divergent, so heißt die Reihe R bedingt konvergent. Man kann in diesem Fall durch Umstellen der Glieder jede beliebige Zahl zur Summe der Reihe machen. Kommt in den Gliedern der Reihe eine Veränderliche x vor, so kann die Reihe bei gewissen Werten von x konvergent, bei andern divergent sein. Eine Reihe heißt alsdann in einem gewissen Gebiet der Veränderlichen x gleichmäßig konvergent, wenn man, nach Wahl einer beliebig kleinen Größe ε, den Stellenzeiger n, bei welchem das Restglied kleiner wird als ε, von x unabhängig wählen kann. Die Reihe hört dagegen auf, gleichmäßig konvergent zu sein, wenn die Summe der Reihe eine unstetige Funktion ist; dabei können die Glieder selbst stetige Funktionen von x sein. Innerhalb des Konvergenzgebiets der nicht gleichmäßig konvergenten Reihe können einzelne Divergenzstellen existieren, was bei gleichmäßig konvergenten Reihen nicht möglich ist. In der Nähe einer solchen Stelle konvergiert die Reihe unendlich langsam. Eine divergente Reihe heißt halbkonvergent (semikonvergent), wenn ihre Summe bis zu einer gewissen Gliederzahl sich einem bestimmten Grenzwert nähert, bei Hinzunahme weiterer Glieder sich wieder von demselben entfernt. An der Stelle der größten Annäherung erreicht das Restglied, als Funktion des Stellenzeigers betrachtet, ein Minimum. Eine divergierende Reihe heißt unbedingt divergent, wenn ihre Summe einen unendlichen Grenzwert hat, z.B. 1 + ¹/₂ + ¹/₃ + ¹/₄ oder 1 – 2 + 4 – 8 + – ...; sie heißt bedingt divergent oder oscillierend, wenn ihre Summe zwischen zwei endlichen Grenzwerten hin und her schwankt, z.B. 1 – 1 + 1 – 1 + – ... Das Rechnen mit divergenten Reihen ist unzulässig.

C. Konvergenzkriterien. So heißen die Kennzeichen, vermitteln: deren man über Konvergenz oder Divergenz der Reihen entscheidet. Kriterium von Leibniz: eine Reihe mit abwechselnden Vorzeichen konvergiert, wenn die absoluten Beträge der Glieder gegen Null abnehmen. I. Kriterium von Gauß: Die Reihe u₁ + u₂ + u₃ + ... + u_n + u_{n + 1} ... konvergiert bezw. divergiert, je nachdem lim

Dann ist auch (nach Cauchy)

II. Kriterium von Gauß: Ist

so konvergiert die Reihe, wenn

Kriterium von Raabe: Eine Reihe konvergiert, wenn

Logarithmisches Kriterium von Cauchy: Konvergenz oder Divergenz, je nachdem

Divergenzkriterium von Olivier: Divergenz, wenn

Kriterium von Kummer: Ist φ(n) eine beliebige positive Funktion von n, so hat man Konvergenz, wenn

Cauchysches Ausschnittkriterium: Die Reihe u₀ + u₀ + ... + u_m + u_{m + 1} + ... + u_n konvergiert, wenn man m und n so wählen kann, daß

[398] D. Potenzreihen [3], [4]. So heißen Reihen, welche nach steigenden oder fallenden Potenzen der Veränderlichen fortschreiten; z.B. a₀ + a₁ x + a₂ x² + ... Eine solche konvergiert unbedingt und gleichmäßig für alle x < A, wo

Da eine Reihe mit komplexen Gliedern konvergiert, wenn die Reihe gebildet aus den absoluten Beträgen (Moduln) der Glieder konvergiert, so ist die Potenzreihe konvergent für alle x, deren absolute Beträge kleiner als der absolute Betrag von A sind. Ordnet man einer komplexen Zahl a + b i den Punkt a, b der Ebene zu, so liegen die zu den Werten von x, für die die Potenzreihe konvergiert, gehörigen Punkte innerhalb eines Kreises, der um den Ursprung mit dem absoluten Betrag von A als Radius beschrieben wird und Konvergenzkreis heißt. Die Potenzreihe stellt innerhalb des Konvergenzkreises eine stetige Funktion dar. – Der Konvergenzkreis geht durch den dem Ursprung zunächst gelegenen Unstetigkeitspunkt der Funktion. Er kann auch unendlich groß sein, wie bei 1 + x/1! + x²/2! + x³/3! + ... der unendlich klein, wie bei 1 + x · 1! + x² · 2! + + ... Auf dem Konvergenzkreis ist die Reihe im allgemeinen divergent. Die geometrische Reihe 1/(1 – x) = 1 + x + x² + x³ + ... hat den Unstetigkeitspunkt x = 1 und divergiert daher auch für x = – 1, obgleich an dieser Stelle die Funktion 1/(1 – x) stetig ist. Eine Potenzreihe darf differentiiert werden; sie bleibt alsdann stetig innerhalb des Konvergenzkreises. Außerhalb des letzteren ist die Funktion durch die Potenzreihe zunächst nicht bestimmt. Ist jedoch a ein Punkt innerhalb des Konvergenzkreises, so kann die Funktion auch nach Potenzen von x – a entwickelt werden. Diese Reihe konvergiert innerhalb eines Kreises um a, der durch den nächstgelegenen Unstetigkeitspunkt hindurchgeht. Das neue Konvergenzgebiet hat einen Teil mit dem alten gemein, wodurch die Identität der durch beide Entwicklungen dargestellten Funktionen bewiesen wird. Es ragt aber im allgemeinen auch über dasselbe hinaus, wodurch die Funktion über den ursprünglichen Konvergenzkreis hinaus fortgesetzt ist. Dieses Verfahren kann wiederholt werden, und so ist es möglich, durch derart ineinander fortsetzbare Potenzreihen, Funktionselemente genannt, die Funktion überall da, wo sie stetig ist, in der ganzen Ebene zu definieren. Im Ausnahmefall, da die Unstetigkeitspunkte der Funktion eine geschlossene Kurve überall dicht erfüllen, entsteht eine Funktion mit natürlichen Grenzen.

E. Besondere Potenzreihen [5]. Eine Potenzreihe heißt rekurrent von der k-ten Ordnung, wenn jeder Koeffizient eine vom Stellenzeiger unabhängige lineare Funktion der k vorhergehenden ist, d.h. a₀ + a₁ x + a₂x² + ... ist rekurrierend, wenn a_n = α₁a_{n – k} + α₂ a_{n – k + 1} + ... α_k a_{n – 1}. Durch Summierung einer solchen Reihe entsteht eine echtgebrochene rationale Funktion, deren Nenner von der k-ten Ordnung ist. Die rekurrierenden Reihen erster Ordnung sind die geometrischen Reihen von der Form 1 + α x + α² x² + ... Die hypergeometrischen Reihen (s.d.) sind von der Form

Eine Funktion kann nur auf eine Weise in eine Potenzreihe entwickelt werden. Hat man daher zwei Entwicklungen für eine Funktion, so müssen die Koeffizienten gleichhoher Potenzen in beiden gleich sein (Satz von Leibniz). Ist F(x) eine Funktion von x, so lautet die Taylorsche Reihe:

wo

das sogenannte Restglied ist (ϑ ist eine Zahl zwischen 0 und 1). Dasselbe kann auch geschrieben werden:

Mit x = 0 und h = x folgt hieraus die Maclaurinsche Reihe:

F. Entwicklung von Funktionen in Potenzreihen. Hierzu dienen die Taylorsche und die Maclaurinsche Reihe. Beispiele:

a) Binomialreihe

Dieselbe ist unendlich für jedes negative oder gebrochene m und konvergiert für –1 < x < + 1, ferner für x = 1, wenn m > –1.

b) Exponentialreihe

Sie konvergiert für jedes endliche x.[399]

c) Logarithmische Reihe

Sie konvergiert für –1 < x < + 1. Dieselbe dient zur Berechnung der Logarithmen. Es ist nämlich

hieraus

zur Berechnung von l(N + h), wenn l N bekannt ist. Um statt der natürlichen Logarithmen die gewöhnlichen zu erhalten, hat man die rechte Seite dieser Gleichung mit dem Modul M zu multiplizieren. Dabei ist

d) Sinusreiche

Sie konvergiert für jedes endliche x. Dasselbe gilt von der Cosinusreihe

e) Die Arcussinusreihe ist

Sie konvergiert für –1 x + 1.

f) Die Arcustangensreihe

konvergiert für –1 x + 1.

g) Die Reihen für die hyperbolischen Funktionen sind:

Hier sind B₁B₂ ... die Bernoullischen, E₀E₂E₄ ... die Eulerschen Zahlen.

G. Trigonometrische (periodische) Reihen, s. Fouriersche Reihen.

H. Produktenreihen. Ein Produkt mit unendlich vielen Faktoren

Π = (1 + a₀)(1 + a₁)(1 + a₂)...

heißt konvergent, wenn es sich mit wachsender Faktorenzahl einem von Null und Unendlich verschiedenen Grenzwert nähert. Die notwendige und hinreichende Bedingung hierfür ist, daß die Summenreihe Σ = a₀ + a₁ + a₂ + ... konvergiert. Weiteres über Produktenreihen s. Produkte, unendliche, und Fakultäten.

J. Teilbruchreihen [12] heißen solche Reihen von Brüchen, bei welchen jeder der letzteren ein aliquoter Teil des vorhergehenden ist. Bei den einfachen Teilbruchreihen haben alle Brüche den Zähler 1. Eine solche ist daher 1/a + 1/a b + 1/a b c + ... Sie kann in einen auflegenden Kettenbruch verwandelt werden

Beide Kettenbrüche haben dieselben Näherungsbrüche. Eine Teilbruchreihe heißt Kettenreihe, wenn die Nenner Potenzen einer Grundzahl a sind, z.B. α/a + β/a² + γ/a³ ... Für a = 10 heißt eine solche Kettenreihe Dezimalbruch.

Literatur: [1] Catalan, E., Traité élémentaire des séries, Paris 1860. – [2] Hagen, G., Synopsis der höheren Mathematik, Bd. 1, Berlin 1891, Abschn. 4 und 5. – [3] Biermann, O., Theorie der analytischen Funktionen, Leipzig 1887, Kap. 3, Abschn. 1. – [4] Forsyth, A.R., Theory of functions of a complex variable, Cambridge 1893, Kap. 2. – [5] Serret, Lehrbuch[400] der Differential- und Integralrechnung, deutsch von Harnack, Bd. 1, Kap. 5. – [6] Reiff, Geschichte der unendlichen Reihen, Tübingen 1889. – [7] Schrader, Theorie der endlichen summierbaren Reihen, Halle 1871. – [8] Schmidt, Von der Konvergenz und Divergenz unendlicher Reihen, Cöln 1867. – [9] Schneidewind, Ueber Konvergenz unendlicher Reihen, Freiburg 1868. – [10] Schimpf, Eine Theorie der Konvergenz unendlicher Reihen, Bochum 1895. – [11] Simon, Die harmonische Reihe, Halle 1886. – [12] Decker, Ueber Teilbruchreihen, I u. II, Troppau 1865–67. – [13] Laurent, Théorie des séries, Paris 1864. – [14] Godefroy, Théorie élémentaire des séries, Paris 1903. – [15] Druckenmüller, Theorie der Kettenreihen, Trier 1837. – [16] Runge, Theorie und Praxis der Reihen, Leipzig 1904.

Wölffing.