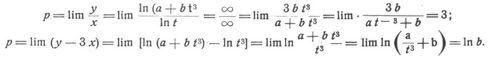Asymptote
[330] Asymptote einer Kurve heißt jede nicht ganz im Unendlichen liegende Tangente derselben, deren Berührungspunkt unendlich entfernt ist. Die Kurve nähert sich einer solchen unaufhörlich, ohne sie, theoretisch gesprochen, im Endlichen zu erreichen. Jedoch kann die Annäherung eine so schnelle sein, daß, wenn die Kurve in irgend einem bestimmten Maßstab gezeichnet ist, sie sich bald von der Asymptote nicht mehr unterscheiden läßt. Es werden bisweilen auch krummlinige Asymptoten in Betracht gezogen, vgl. [1] oder [2].
Bezüglich der Bestimmung der Asymptoten einer ebenen Kurve sind mehrere Fälle zu unterscheiden.[330]
a) Ist die Kurve durch zwei Gleichungen x = f1(t), y = f2(t) gegeben, so suche man sämtliche Werte von t, für die x oder y unendlich wird. Wenn für einen solchen Wert bloß x oder bloß y unendlich wird, dagegen y resp. x einen bestimmten endlichen Wert b resp. a annimmt, so ist y = b resp. x = a die Gleichung einer Asymptote der Kurve. Werden für einen Wert t = τ sowohl x als y unendlich, und setzt man die Gleichung der zugehörigen Asymptote in der Form y = px + q voraus, so ist
Beispiel:
Es wird x unendlich für t = ± 1, y für dieselben Werte und außerdem für t = 0. Für letzteren Wert erhält man x = c, als Gleichung einer Asymptote. Weiter ergibt sich für t = +1:
folglich als Gleichung der zugehörigen Asymptote y = x + c/2. Für t = –1 findet man auf ähnliche Weise y = –x – c/2.
b) Die Fälle, in denen die Kurve durch eine einzige Gleichung der Form y = f(x) oder x = f(y) gegeben ist, kommen auf den vorigen zurück, wenn man im ersten x, im zweiten y gleich t oder auch gleich einer Funktion von t setzt. (Wird die Einführung der neuen Veränderlichen t unterlaufen, so ist bei transzendenten Kurven darauf zu achten, daß für den Wert +∞ von x resp. y sich eine andre Asymptote ergeben kann als für den Wert –∞. Vgl. das folgende Beispiel.) Es lassen sich diese Fälle auch dem folgenden unterordnen, also nach den unter c) angegebenen Methoden behandeln. Beispiel: y = ln(a + be3x), a und b positiv. Man könnte x = t setzen, zweckmäßiger ist es aber, x = lnt zu nehmen, wodurch man e3x = t3, y = ln(a + bt3) erhält. Es wird x unendlich für t = 0 und t = ∞, y dagegen für t = ∞ und t = –∛a/b, wovon der letztere Wert nicht in Betracht kommt, weil zu ihm ein imaginärer Wert von x gehört. Für t = 0 ergibt sich y = ln a als Gleichung einer Asymptote. Für t = ∞ findet man
Also ist y = 3x + lnb die Gleichung der zweiten Asymptote.
c) Wenn die Kurve durch eine Gleichung F (x, y) = 0 gegeben ist, so kann man in dieser x = r cos φ, y = r sin φ und (nötigenfalls nach Division mit einer passenden Potenz von r oder einer sonstigen Umformung, die das Auftreten unendlich werdender Glieder verhütet) r = ∞ setzen; jede Wurzel der entstehenden Gleichung für φ gibt dann den Winkel einer Asymptote der Kurve mit der x-Achse an. Ist einer dieser Winkel gleich einem Rechten, so hat die Gleichung der zugehörigen Asymptote die Form x = a; man bestimmt a durch Auflösung der Gleichung in x, die sich ergibt, wenn in F (x, y) = 0 y = ∞ gesetzt wird. (Unter Umständen muß eine Umformung der Gleichung vorausgehen, die bewirkt, daß für y = ∞ alle Glieder derselben endlich bleiben.) In jedem andern Falle schreibe man die Gleichung der Asymptote in der Form y = px + q; es ist dann p = tg φ und q muß aus der Gleichung berechnet werden, die aus F(x,y) = 0 entsteht, wenn man darin (px + q) an Stelle von y und hierauf – wiederum nach allenfalls nötigen Umformungen –x = ∞ setzt.
Beispiel: F (x, y) = x2y + xy2 – c = 0.
Durch Einsetzen von x = r cos φ, y = r sin φ und Division mit r3 erhält man
cos φ sin φ (cos φ + sin φ) – c/r3 = 0,
also für r = ∞:
cos φ sin φ (cos φ + sin φ) = 0.
Diese Gleichung zerfällt in folgende drei:
cos φ = 0, sin φ = 0, cos φ + sin φ = 0.
Die erste der letzteren Gleichungen liefert φ gleich einem rechten Winkel. Dividiert man die Gleichung der Kurve mit y2 und setzt dann y = ∞, so kommt x = 0, das daher die Gleichung einer Asymptote ist. Die andern beiden Gleichungen für φ ergeben
φ = 0, also tg φ = 0, und tg φ = –1,
so daß man y = q und y = –x + q erhält. Setzt man der Reihe nach diese Werte von y in die Gleichung der Kurve ein, dividiert durch x2 und läßt dann x unendlich werden, so kommt beidemale q = 0. Die Gleichungen der zweiten und dritten Asymptote der Kurve sind daher y = 0 und y = – x.
Für algebraische Kurven gibt es einige besondere Methoden zur Ermittlung der Asymptoten, bezüglich derer auf [1], [2], [3] und [4] verwiesen werden kann. In [3] und [4] findet man auch geometrische Sätze über die Asymptoten höherer algebraischer Kurven nebst Literaturangaben.
d) Liegt eine Gleichung F (r, φ) = 0 zwischen Polarkoordinaten vor, so läßt man in derselben r unendlich werden (erforderlichenfalls nach Division mit einer gewissen Potenz von r,[331] vgl. die vorhergehenden Fälle); die Wurzeln der sich ergebenden Gleichung für φ sind die Winkel zwischen den Asymptoten der Kurve und der Polarachse. Berechnet man für einen solchen Wert von γ den Ausdruck
so erhält man den Abstand der betreffenden Asymptote vom Anfangspunkt des Koordinatensystems.
Beispiel: Die Gleichung der hyperbolischen Spirale ist rφ – c = 0. Dividiert man dieselbe durch r und setzt hierauf r = ∞, so kommt φ = 0, d.h. die Kurve besitzt eine zur Polarachse parallele Asymptote. Durch Ableitung obiger Gleichung nach r ergibt sich
also ist
Somit befindet sich die Asymptote im Abstand c von der Polarachse und zwar (wegen des Minuszeichens) auf der negativen Seite derselben. (Das Einsetzen von φ = 0 und r = ∞ kommt hier in Wegfall, weil r2dφ/dr konstant ist). – Zahlreiche weitere Uebungsbeispiele enthalten [5] und [6]. Die Bestimmung der Asymptoten räumlicher Kurven erfolgt nach ähnlichen Grundsätzen; es kann hier namentlich das unter a) Gesagte als Anhalt dienen.
Literatur: [1] Johnson, W.W., Curve tracing in Cartesian coordinates, New York 1884. – [2] Reuschle, C., Praxis der Kurvendiskussion, Stuttgart 1886. – [3] Salmon, G., und Fiedler, W., Analytische Geometrie der höheren ebenen Kurven, 2. Aufl., Leipzig 1882. – [4] Hagen, J.G., Synopsis der höheren Mathematik, Bd. 2, Geometrie der algebraischen Gebilde, Berlin 1884. – [5] Schlömilch, O., Uebungsbuch zum Studium der höheren Analysis, 4. Aufl., Leipzig 1887. – [6] Sohncke, L.A., Sammlung von Aufgaben aus der Differential- und Integralrechnung, Bd. 1, 6. Aufl., Halle a. S. 1903.
Mehmke.
Buchempfehlung
Angelus Silesius
Cherubinischer Wandersmann
Nach dem Vorbild von Abraham von Franckenberg und Daniel Czepko schreibt Angelus Silesius seine berühmten Epigramme, die er unter dem Titel »Cherubinischer Wandersmann« zusammenfasst und 1657 veröffentlicht. Das Unsagbare, den mystischen Weg zu Gott, in Worte zu fassen, ist das Anliegen seiner antithetisch pointierten Alexandriner Dichtung. »Ich bin so groß als Gott, er ist als ich so klein. Er kann nicht über mich, ich unter ihm nicht sein.«
242 Seiten, 11.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Geschichten aus dem Biedermeier III. Neun weitere Erzählungen
Biedermeier - das klingt in heutigen Ohren nach langweiligem Spießertum, nach geschmacklosen rosa Teetässchen in Wohnzimmern, die aussehen wie Puppenstuben und in denen es irgendwie nach »Omma« riecht. Zu Recht. Aber nicht nur. Biedermeier ist auch die Zeit einer zarten Literatur der Flucht ins Idyll, des Rückzuges ins private Glück und der Tugenden. Die Menschen im Europa nach Napoleon hatten die Nase voll von großen neuen Ideen, das aufstrebende Bürgertum forderte und entwickelte eine eigene Kunst und Kultur für sich, die unabhängig von feudaler Großmannssucht bestehen sollte. Für den dritten Band hat Michael Holzinger neun weitere Meistererzählungen aus dem Biedermeier zusammengefasst.
- Eduard Mörike Lucie Gelmeroth
- Annette von Droste-Hülshoff Westfälische Schilderungen
- Annette von Droste-Hülshoff Bei uns zulande auf dem Lande
- Berthold Auerbach Brosi und Moni
- Jeremias Gotthelf Die schwarze Spinne
- Friedrich Hebbel Anna
- Friedrich Hebbel Die Kuh
- Jeremias Gotthelf Barthli der Korber
- Berthold Auerbach Barfüßele
444 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum