Schwedlerträger [1]
[840] Schwedlerträger heißen Balkenfach werke (s.d.) mit einer Oeffnung, deren Vertikalenlängen, abgesehen von einigen Feldern um die Mitte, aus der Bedingung folgen sollten, daß die Diagonalen bei bewegter Last nur Zug erleiden und ihre unteren Grenzbeanspruchungen gleich Null oder doch annähernd so groß sind. Die beiden Gurtungen treffen sich an den Auflagern. Derartige Träger hat Schwedler (Berlin) eingeführt, um die Diagonalen aus Flacheisen herstellen zu können und doch Gegendiagonalen (s.d.) möglichst zu vermeiden. Dies läßt sich zwar auch durch Dreiecksträger (s.d.) und Parallelträger (s.d.) erreichen, nicht aber z.B. durch Parabelträger (s.d.), deren Form sich der Schwedlerträger nähern sollte. Daneben nahm man eine erhebliche Materialersparnis an, die z.B. Winkler anfangs gegenüber dem Parabelträger von gleicher Höhe zu etwa 10%, gegenüber dem Parallelträger von 4/5 so großer Höhe zu ca. 30% berechnete (Winkler, Die Gitterträger, Wien 1875, S. 17; s.a. Zeitschr. d. Ver. deutsch. Ing. 1877, S. 221; vgl. [8], S. 199).
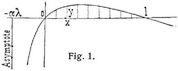
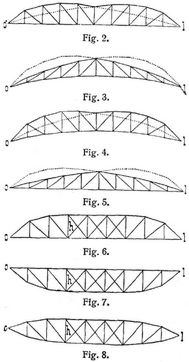
Theoretisch kann die Form der einen Gurtung frei gewählt werden, wonach die der andern durch die bedingungsgemäße Länge der Vertikalen bestimmt ist Werden, z.B. Eigengewicht und Verkehrslast auf die ergriffenen Strecken gleichmäßig verteilt angenommen, so ergeben sich die Vertikalenlängen an beliebigen Stellen x gleich den Ordinaten y eines Hyperbelbogens (Fig. 1), der bei den Auflagern 0 und l die Abszissenachse schneidet und außerhalb der Spannweite eine vertikale Asymptote hat [6], [9], S. 138. (Der mitunter verwendete Name Hyperbelträger [6], [8], S. 175, ließe sich hiernach immerhin höchstens bei der Berechnung für gleichmäßig verteilte Lasten begründen.) Ein solcher Träger für gleichmäßig verteilte Lasten wie für bewegte Radlastzüge wäre aber nicht symmetrisch zur Mitte. Durch Umklappen der ersten Hälfte um die Mitte entsteht ein Träger, dessen eine Gurtung bei der Mitte eine einspringende Ecke besitzt (Fig. 2, 4), während der durch Umklappen der zweiten Hälfte entstehende Träger (Fig. 3, 5) dem Dreiecksträger gegenüber keine Vorteile bietet. Um die einspringende Ecke zu vermeiden, hat Schwedler ein Stück Parallelträger eingeschaltet (Fig. 6–8). Indem man damit von der Grenzform einfacher Zugdiagonalen abweicht, können einfache Diagonalen in den betreffenden.[840] Feldern abwechselnd Zug und Druck erhalten, und sollen sie nur auf Zug widerstandsfähig werden, so müssen Gegendiagonalen zur Verwendung kommen. Da überdies der Untergurt stets horizontal ausgeführt wurde, so stellt Fig. 6 den gewöhnlichen Schwedlerträger dar.
Der Symmetrie halber genügt es, die erste Trägerhälfte zu berechnen. Die Felderzahl n und größte Trägerhöhe h können den konstruktiven Bedürfnissen entsprechend frei gewählt werden. Die Form des Trägers hängt wesentlich vom Verhältnis des Eigengewichts zur Verkehrslast ab. Ersteres möge mit g pro Längeneinheit als gleichmäßig verteilt auf die Spannweite l = n λ gelten. Da der Wert von g im voraus nicht genau bekannt ist, so tut man gut, für die Formberechnung einen etwas kleineren Wert g1 zu wählen, als man sonst annehmen würde und für die nachfolgende Berechnung der Beanspruchungen annehmen wird. Als rechnungsmäßige untere Grenzbeanspruchung der Diagonalen ergibt sich dann nicht Null, sondern ein geringer Zug proportional g – g1 so daß die gewünschte Vermeidung von Druckbeanspruchungen um so sicherer (eventuell selbst bei Stößen) erreicht wird. Selbstverständlich könnte man in den folgenden Formeln auch g1 = g setzen und damit die rechnungsmäßigen unteren Grenzbeanspruchungen der Diagonalen gleich Null erlangen.
Es handle sich um die Formberechnung für eine gleichmäßig verteilte bewegte Last von p pro Längeneinheit der ergriffenen Strecke; hm sei die Länge der m ten Vertikale vom Auflager 0 aus und
α = n · g1/p.
1.
Wird von vornherein eine gewisse Anzahl Felder mit parallelen Gurtungen angenommen, so folgt von der diesen Teil begrenzenden Vertikale hm = h an gegen 0 hin eine Vertikalenlänge aus der andern mittels der Gleichung
Sollte sich hierbei die erste berechnete Vertikale länger als h ergeben, so wären nicht genug Felder mit parallelen Gurtungen gewählt. Um nicht ein Feld unnötig mit solchen zu versehen, kann man auch den Index m der längsten Vertikale in Fig. 1 berechnen aus
und den von dieser an nach der Trägermitte hin gelegenen Vertikalen die gleiche Länge h geben. Nachdem die Trägerform festgestellt ist, lassen sich die Grenzwerte der Stabkräfte nach den für einfache Balkenfachwerke mit beliebigen Gurtungsformen bestehenden Formeln berechnen (Bd. 1, S. 528; [9], S. 108, 111). Für das Parallelträgerstück, ausschließlich seiner Grenzvertikalen, gelten auch die Formeln für Parallelträger (S. 34; [9], S. 116, 118), während für die übrigen Vertikalen die Beanspruchungen Dm durch das Eigengewicht und die Grenzbeanspruchungen auch ausgedrückt sind:
worin dm die Diagonalenlänge, q = g + p und
Ueber den Einfluß der Gegendiagonalen beim Schwedlerträger s. Bd. 4, S. 342, und [9], S. 163.
In ganz analoger Weise wie für gleichmäßig verteilte bewegte Last läßt sich die Berechnung, für bewegte Radlastzüge durchführen, wobei an Stelle von 1.–5. etwas andre Ausdrücke treten [9], S. 144. Für Schwedlerträger von Eisenbahnbrücken empfiehlt sich die Berechnung mit Radlastzügen; bei obigem Verfahren müßten die Lastäquivalente p für die Formberechnung und die Beanspruchungen der Füllungsglieder erheblich größer als für die Beanspruchungen der Gurtungen gewählt werden, wenn nicht unbeabsichtigter Druck in den Diagonalen entstehen sollte [10], S. 266. Beispiele der Berechnung von Schwedlerträgern für gleichmäßig verteilte bewegte Last s. [10], S. 254, für bewegte Radlastzüge [10], S. 259, für genaue Lastäquivalente von Radlastzügen [10], S. 265. Ueber Bruchversuche mit Schwedlerträgern s. Bd. 3, S. 537, und [12].
Die ersten Schwedlerträger, jedoch von doppeltem System (Bd. 3, S. 543) und nicht genau obiger Bedingung entsprechend, erhielt die Weserbrücke bei Corvey und Höxter 1867 [1], worauf sofort eine Oderbrücke bei Stettin [1] und, besonders in Norddeutschland, zahlreiche weitere Ausführungen folgten. Gegenwärtig kommen solche Träger aus ästhetischen Gründen seiten zur Verwendung. Anstatt Schwedlerträger hat man vereinzelt Ellipsenträger (s.d.) gewählt, bei welchen ebenfalls durch Einschalten eines Parallelträgerstücks Gegendiagonalen im übrigen Teile vermieden werden können und der Materialverbrauch etwa der gleiche ist [8], S. 210. Träger nach der Grenzform einfacher Zugdiagonalen bis zur Mitte entsprechend Fig. 4 hat Launhardt anwenden wollen [5], um Gegendiagonalen vollständig zu vermeiden, doch sind solche wegen ihrer unschönen und bezüglich der Gurtungsbeanspruchungen unzweckmäßigen Form, auf die schon Schwedler hinwies [1], S. 250, nie ausgeführt worden.
Literatur: [1] Schwedler, Schmiedeeiserne Brücken nach J.W. Schwedlers System, Deutsche Bauztg. 1867, S. 250 (Weiteres über die Weserbrücke bei Corvey: Zeitschr. f. Bauw. 1867, S. 182). – [2] Ders., Die kurze und lange Oderbrücke in Breslau, Zeitschr. f. Bauw. 1868, S. 157 (vgl. Meyerhoff, Die Schwedlerbrücken in Breslau, Zeitschr. d. Ver. deutsch. Ing. 1896, S. 202). – [3] Ders., Der eiserne Unterbau für die großen Oeffnungen der Brücke über die Elbe in der Berlin-Lehrter Eisenbahn (bei Hämerten), Zeitschr. für Bauwesen 1868, S. 517. – [4] Schäffer, Graphische Ermittlung der Ordinaten und Grenzspannungen des Schwedlerschen Trägers, ebend. 1874, S. 391 (s.a. 1873, S. 237, 523). – [5] Launhardt, Neue Modifikation des Schwedlerträgers, Deutsche Bauztg. 1876, S. 61, 101, 121, 176, 211, 245 (s.a. Quietmeyer, Zeitschr. d. Arch.- u. Ing.-Ver. zu Hannover 1877, S. 233). – [6] Kayser, Ueber die Grundform des sogenannten Schwedlerträgers,[841] Zeitschr. d. Ver. deutsch. Ing. 1877, S. 529 (Hyperbelträger). – [7] Stelzel, Theorie einfacher statisch bestimmter Brückenträger, Wien 1880, S. 268–285. – [8] Winkler, Theorie der Brücken, II. Theorie der gegliederten Balkenträger, Wien 1881, S. 175–202. – [9] Weyrauch, Theorie der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1887, S. 136–145, 163. – [10] Ders., Beispiele und Aufgaben zur Berechnung der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1888, S. 254–268. – [11] Ritter, Anwendungen der graphischen Statik, II. Das Fachwerk, Zürich 1890, S. 67. – [12] Bruchbelastung an der Neißebrücke bei Forst, Zeitschr. für Bauwesen 1895, S. 289. – [13] Schurich, Ueber die Berechnung der Grenzspannungen der Gitterstäbe eines einfachen Fachwerkbalkens und den Entwurf eines Schwedlerträgers, Zeitschr. für Architektur und Ingenieurwesen 1898 (Wochenausg.), S. 179. – [14] Müller-Breslau, Die graphische Statik der Baukonstruktionen, I, Leipzig 1901, S. 288. – [15] Handbuch der Ing.-Wiss., II. Der Brückenbau, 2. Abt., Leipzig 1901, S. 322. – [16] Keck-Hotop, Vorträge über Elastizitätslehre, II, Hannover 1908, S. 289.
Weyrauch.
Lueger-1904: Schwedlerträger [2]
Buchempfehlung
Schnitzler, Arthur
Der grüne Kakadu. Groteske in einem Akt
In Paris ergötzt sich am 14. Juli 1789 ein adeliges Publikum an einer primitiven Schaupielinszenierung, die ihm suggeriert, »unter dem gefährlichsten Gesindel von Paris zu sitzen«. Als der reale Aufruhr der Revolution die Straßen von Paris erfasst, verschwimmen die Grenzen zwischen Spiel und Wirklichkeit. Für Schnitzler ungewöhnlich montiert der Autor im »grünen Kakadu« die Ebenen von Illusion und Wiklichkeit vor einer historischen Kulisse.
38 Seiten, 3.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Romantische Geschichten II. Zehn Erzählungen
Romantik! Das ist auch – aber eben nicht nur – eine Epoche. Wenn wir heute etwas romantisch finden oder nennen, schwingt darin die Sehnsucht und die Leidenschaft der jungen Autoren, die seit dem Ausklang des 18. Jahrhundert ihre Gefühlswelt gegen die von der Aufklärung geforderte Vernunft verteidigt haben. So sind vor 200 Jahren wundervolle Erzählungen entstanden. Sie handeln von der Suche nach einer verlorengegangenen Welt des Wunderbaren, sind melancholisch oder mythisch oder märchenhaft, jedenfalls aber romantisch - damals wie heute. Michael Holzinger hat für den zweiten Band eine weitere Sammlung von zehn romantischen Meistererzählungen zusammengestellt.
- Novalis Die Lehrlinge zu Sais
- Adelbert von Chamisso Adelberts Fabel
- Jean Paul Des Feldpredigers Schmelzle Reise nach Flätz
- Clemens Brentano Aus der Chronika eines fahrenden Schülers
- Friedrich de la Motte Fouqué Eine Geschichte vom Galgenmännlein
- E. T. A. Hoffmann Der goldne Topf
- Joseph von Eichendorff Das Marmorbild
- Ludwig Achim von Arnim Die Majoratsherren
- Ludwig Tieck Die Gemälde
- Wilhelm Hauff Die Bettlerin vom Pont des Arts
428 Seiten, 16.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum