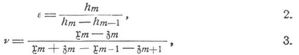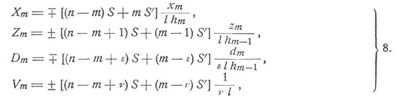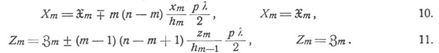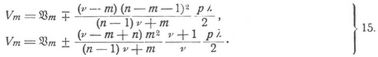Balkenfachwerke
[526] Balkenfachwerke heißen in der Ingenieurmechanik Balkenträger (s. Balken), die als Fachwerke (s.d.) gegliedert sind. Man unterscheidet demnach einfache Balkenfachwerke (über eine Oeffnung) und durchlaufende Balkenfachwerke über mehrere Oeffnungen, Balkenfachwerke einfachen Systems und mehrfachen Systems. Wird ein Balkenfachwerk, an dem nur Lasten oder sonstige vertikale Aktivkräfte angreifen, durch einen beliebig geformten Schnitt s in zwei Teile zerlegt gedacht, so in die resultierende Horizontalkraft, mit welcher der eine Teil auf den andern wirkt, stets Hs = 0 (Näheres s. Schnittkräfte). Da Allgemeines über die Berechnung der Fachwerke unter dem Stichwort Fachwerke (auch statisch bestimmte, statisch unbestimmte und mehrfachen Systems) zu geben ist und die wichtigsten Fälle unter Dreieck-, Parabel-, Parallelträger, Paulischer Träger, Schwedlerträger u.s.w. vorkommen, so sollen hier nur für das am häufigsten auftretende einfache System mit beliebigen Gurtungsformen, das sogenannte Ständerfachwerk, Formeln gegeben werden, die bei bekannten äußeren Kräften (s.d.) unmittelbar verwendbar sind.
Der Träger sei innerhalb der Spannweite l (zwischen den Auflagern 0 und l) durch Vertikalen in n Felder von gleichen Längen λ geteilt. In jedem Felde befindet sich eine wirksame Diagonale, die zweierlei Stellungen einnehmen kann. Es werden die in Fig. 1 und 2 ersichtlichen Bezeichnungen eingeführt (wonach diejenige Gurtung als X-Gurtung bezeichnet ist, die man trifft, wenn man einer Diagonale nach der Seite von Auflager 0 hin folgt). xm, zm, dm, hm seien die Längen der Stäbe, die durch Xm, Zm, Dm, Vm beansprucht sind, für ein rechtwinkliges Koordinatensystem mit dem Ursprung im Auflager 0 und horizontaler Abszissenachse mögen xm, zm die Koordinaten der Knotenpunkte m (d.h. der Knotenpunkte bei Abszisse mλ) in X-Gurtung und Z-Gurtung bedeuten. Dann gelten in allen folgenden Ausdrücken der Stabkräfte die oberen Vorzeichen bei obenliegender X-Gurtung (Fig. 1), die unteren Vorzeichen bei untenliegender X-Gurtung (Fig. 2). Kommen andre als vertikale äußere Kräfte vor, so bestehen die unter Fachwerke, statisch bestimmte, gegebenen Gleichungen 7.–10. Für beliebige Belastung (vertikale Aktivkräfte) hat man:
worin bei beliebigen Gurtungsformen:
und speziell bei horizontaler X-Gurtung (Fig. 3 und 4):
xm = λ, v = hm/(hm + 1 – hm),
4.
bei horizontaler Z-Gurtung (Fig. 5 und 6):
zm = λ, v = ε,
5.
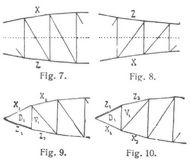
bei symmetrischen Gurtungen (zu einer Horizontalen, Fig. 7 und 8):
zm = xm, v = (2hm)/(hm + 1 – hm – 1)
6.
[526] Weiter bedeuten M, M' die statischen Momente aller äußeren Kräfte vor einem Vertikalschnitt 0 durch Auflager 0 bezw. nach einem Vertikalschnitt l durch Auflager l in bezug auf diese Auflager, und S, S' die statischen Momente der zwischen den Schnitten 0 und s bezw. s und l auf den Träger übertragenen Lasten hinsichtlich der Auflager 0 und l. Hierbei ist Schnitt s (Fig. 1 und 2) für die Berechnung von Xm, Zm, Dm durch das mte Feld, für Vm durch die mit Xm, Vm, Zm + 1 beanspruchten Stäbe gelegt zu denken. Ausdrücke der S, S' für alle Fälle s. [5], §§ 10,18. Die Formeln für Xm, Zm, Dm gelten auch, wenn die Stellung der Diagonalen (und damit die Lage der X-Gurtung) wechselt, während die Formeln für Vm an die Bedingung geknüpft sind, daß der Vertikale m beiderseits Felder mit Diagonalen gleicher Stellung anliegen, wobei jedoch die Diagonale mit einem Gurtungsstabe zusammenfallen kann (Fig. 9 und 10). Für Endvertikalen und Mittelvertikalen kommen also Ausnahmen vor, doch lassen sich deren Stabkräfte leicht aus den Gleichgewichtsbedingungen für die äußeren und inneren Kräfte an den angrenzenden Knotenpunkten ermitteln. Direkt verwendbare Formeln s. [6], A 19, 24, 28. Greift die Fahrbahnlast zwischen beiden Gurtungen in Vertikale m an (Fig. 11 und 12), so ist die Beanspruchung Vm oberhalb und unterhalb der Fahrbahn verschieden. Doch kann bei Berechnung des Vertikalenstücks von Fahrbahn bis X-Gurtung stets so gerechnet werden, als ob die Fahrbahnlast (Eigengewicht und Verkehrslast) in den Knotenpunkten der Z-Gurtung angriffe, bei Berechnung des Vertikalenstücks von Fahrbahn bis Z-Gurtung ganz so, als wenn die Fahrbahnlast in der X-Gurtung angriffe. Näheres s. [5], S. 70. – Soll das Eigengewicht in l mit g pro Längeneinheit als gleichmäßig verteilt auf die Spannweite gelten, und bezeichnen gx, gz diejenigen Teile von g, die auf die Knotenpunkte der X-Gurtung und Z-Gurtung zu rechnen sind, so folgen aus 1. die vom Eigengewicht allein herrührenden Stabkräfte, die wir wie die zugehörigen Momente M, M' zur Unterscheidung durch deutsche Buchstaben bezeichnen:
Greift die Fahrbahnlast zwischen beiden Gurtungen in Vertikale m an (Fig. 11 und 12), so ist dem oben Gesagten zufolge das Eigengewicht der Fahrbahn bei Berechnung des Vertikalenstücks von Fahrbahn bis X-Gurtung in gz, bei Berechnung des Vertikalenstücks von Fahrbahn bis Z-Gurtung in gx einzuschließen. – Die Gleichungen 1.–7. gelten für durchlaufende (kontinuierliche) und einfache Balkenfachwerke des angenommenen Systems. Für erstere wären die Stützenmomente M, M' entweder überschlägig wie bei vollwandigen Trägern zu berechnen (s. Balken und Balken, durchlaufende) oder, wenn größere Genauigkeit erstrebt wird, nach den unter Fachwerke, statisch unbestimmte, angeführten Methoden. Bezüglich der Grenzbeanspruchungen bei bewegter Last s. Grenzwerte, bezüglich des speziell den Parallelträger und die kontinuierlichen Gelenkträger Betreffenden unter diesen Stichworten. Hier mögen spezieller betrachtet werden:
Einfache Balkenfachwerke. Am meisten hat man es mit Balkenfachwerken mit einer Oeffnung und frei drehbaren Enden zu tun, und da für solche M = 0, M' = 0 sind, so folgen aus 1. für beliebige Belastung:
und aus 7. speziell für ein gleichmäßig verteiltes Eigengewicht von g = gx + gz pro Längeneinheit Träger:
[527] Vorstehende Gleichungen liefern die Stabkräfte der angenommenen einfachen Fachwerke für jede gegebene Belastung. Es handle sich nun aber um die Grenzwerte der Stabkräfte bei bewegter Verkehrslast. Letztere betrage p pro Längeneinheit der ergriffenen Strecke. Bezeichnen Xm, Zm, Dm, Bm die Beiträge des beliebigen Eigengewichts der Konstruktion zu Xm, Zm, Dm, Vm, so sind die Grenzbeanspruchungen der Gurtungen:
Wird das Eigengewicht als gleichmäßig verteilt auf die Trägerlänge angesehen, dann hat man wegen 9. die oberen Grenzwerte:
worin q = g + p. Weiter gelten bei beliebigem Eigengewicht für die Grenzbeanspruchungen der Diagonale m:
und für die Grenzbeanspruchungen der Vertikale m:
a) wenn die Fahrbahnlast im Knotenpunkte m der X-Gurtung angreift,
b) wenn die Fahrbahnlast im Knotenpunkte m der Z-Gurtung angreift,
Greift die Fahrbahnlast zwischen beiden Gurtungen in Vertikale m an, so gelten für das Vertikalenstück von Fahrbahn bis X-Gurtung die Gleichungen 14., für das Vertikalenstück von Fahrbahn bis Z-Gurtung die Gleichungen 15.
Wir haben in 13.–15. die Grenzwerte der Stabkräfte für die bei Balkenfachwerken gewöhnlich allein behandelten und fast allein vorkommenden Gurtungsformen gegeben. Die Gleichungen 13. setzen nämlich voraus, daß sich die Richtungslinien der Stäbe xm, zm außerhalb der Spannweite l schneiden (d.h. auch, daß m – ε nicht zwischen 0 und n liegt), und die Gleichungen 14., 15. verlangen, daß sich die Richtungslinien von Xm, Zm + 1 außerhalb der Spannweite l schneiden (oder auch, daß m – ν nicht zwischen 0 und n liegt). Die entsprechenden Gleichungen für Gurtungsformen, die jene Bedingungen nicht erfüllen, s. [5], S. 109. Beispiele der Anwendung obiger Gleichungen [6], B 35, 38, 39, 62, 65, 68, analoge Formeln für bewegte Radlastzüge [5], § 33, mit Beispielen [6], B 36, 63, 66, 69; Formeln für Berechnung mit genauen Lastäquivalenten (s.d.) p an Stelle von Radlastzügen [5], § 32, mit Beispielen [6], B 37, 64, 67, 70. Spezielle Fälle der obigen Formeln s. Parallelträger, Dreieckträger, Parabelträger und [5], Abschnitt III, mit Beispielen [6], Abschnitt III.
Bei den hier betrachteten einfachen Balkenfachwerken werden die Stäbe fast immer symmetrisch zur Trägermitte angeordnet (Formeln für Mittelvertikalen [6], A 28), und zwar besonders häufig so, daß die Diagonalen für Eigengewicht allein Zug erhalten, womit im allgemeinen auch deren obere Grenzbeanspruchungen Zug und die entsprechenden Beanspruchungen der Vertikalen bei den meist vorkommenden Gurtungsformen Druck werden. Eine solche Verteilung von Zug und Druck ist aber bei eisernen Trägern gewöhnlich erwünscht (die Vertikalen pflegen kürzer als die Diagonalen und damit im allgemeinen weniger der Zerknickungsgefahr ausgesetzt zu sein, sie müssen, wenn Querträger anschließen, ohnehin steif konstruiert werden, während die Diagonalen im Falle ihrer Befestigung an Knotenblechen mit Rücksicht auf gleichmäßige Beanspruchung oft zweckmäßig aus Flacheisen bestehen). Stellen nicht beide Grenzbeanspruchungen einer Diagonale Zug dar, die Diagonale soll aber nur für Zug als widerstandsfähig gelten, so ist in dem betreffenden Felde eine Gegendiagonale anzuordnen (s. Fachwerke, Gegendiagonalen).
Literatur: [1] Ritter, Elementare Theorie und Berechnung eiserner Dach- und Brückenkonstruktionen, Hannover 1873. – [2] Stelzel, Theorie einfacher statisch bestimmter Balkenträger, Wien 1880. – [3] Winkler, Theorie der Brücken, 2. Heft: Theorie der gegliederten Balkenträger, Wien 1881. – [4] Müller-Breslau, Die graphische Statik der Brückenkonstruktionen, I, Leipzig 1887. – [5] Weyrauch, Theorie der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1887. – [6] Weyrauch, Beispiele und Aufgaben zur Berechnung der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1888. – [7] Sehfehlner, Beiträge zu den bei eisernen Balkenbrücken vorkommenden Berechnungen, Allgem. Bauztg. 1893, S. 25, 33, 49, 57, 73, 89. – [8] Handbuch der Ingenieurwissenschaften, 2. Bd., 8. Kap.: Theorie der eisernen Balkenbrücken (von Steiner), Leipzig 1901. – [9] Ostenfeld, Technische Statik, Leipzig 1904.
Weyrauch.
Buchempfehlung
Wilbrandt, Adolf von
Gracchus der Volkstribun. Trauerspiel in fünf Aufzügen
Die Geschichte des Gaius Sempronius Gracchus, der 123 v. Chr. Volkstribun wurde.
62 Seiten, 4.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Romantische Geschichten. Elf Erzählungen
Romantik! Das ist auch – aber eben nicht nur – eine Epoche. Wenn wir heute etwas romantisch finden oder nennen, schwingt darin die Sehnsucht und die Leidenschaft der jungen Autoren, die seit dem Ausklang des 18. Jahrhundert ihre Gefühlswelt gegen die von der Aufklärung geforderte Vernunft verteidigt haben. So sind vor 200 Jahren wundervolle Erzählungen entstanden. Sie handeln von der Suche nach einer verlorengegangenen Welt des Wunderbaren, sind melancholisch oder mythisch oder märchenhaft, jedenfalls aber romantisch - damals wie heute. Michael Holzinger hat für diese preiswerte Leseausgabe elf der schönsten romantischen Erzählungen ausgewählt.
- Ludwig Tieck Die beiden merkwürdigsten Tage aus Siegmunds Leben
- Karoline von Günderrode Geschichte eines Braminen
- Novalis Heinrich von Ofterdingen
- Friedrich Schlegel Lucinde
- Jean Paul Die wunderbare Gesellschaft in der Neujahrsnacht
- Adelbert von Chamisso Peter Schlemihls wundersame Geschichte
- E. T. A. Hoffmann Der Sandmann
- Clemens Brentano Die drei Nüsse
- Ludwig Achim von Arnim Der tolle Invalide auf dem Fort Ratonneau
- Wilhelm Hauff Jud Süss
- Joseph von Eichendorff Das Schloß Dürande
442 Seiten, 16.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum