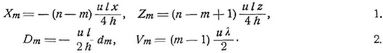Dreieckträger
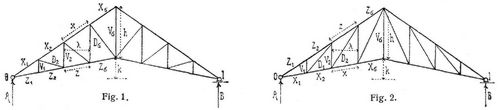
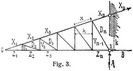
[101] Dreieckträger sind Fachwerke (s.d.), deren Gurtungsachsen entweder der ganzen Länge nach Geraden folgen und sich an einem Trägerende schneiden, oder bei denen die Gurtungsachsen, von einer mittleren Vertikalen ausgehend, gerade Strecken bilden und sich an beiden Trägerenden treffen. Den letzteren Fall hat man z.B. bei den in Fig. 1 und 2 skizzierten englischen Dachbindern, den ersten bei dem in Fig. 3 angedeuteten Perrondachbinder. In statischer Beziehung ist charakteristisch für diese Träger, daß auch bei beliebiger veränderlicher Belastung, ohne Anwendung von Gegendiagonalen (s.d.), kein Stab Wechsel von Zug und Druck erhält, und daß die Beanspruchungen jedes Füllungsgliedes nur von der Belastung der Knotenpunkte zwischen diesem Gliede und demjenigen Trägerende abhängen, an dem sich die angrenzenden Teile der beiden Gurtungsachsen schneiden.
Die Berechnung von Dreieckträgern hat man gewöhnlich für gleichmäßig verteilte Lasten durchzuführen. Es handle sich um einen Träger mit n Feldern von gleichen Längen λ, so daß l = n λ die Spannweite ist, während h die größte Trägerhöhe, dm die Länge der Diagonale im mten Felde bedeuten mögen und weitere Bezeichnungen in Fig. 1–3 ersichtlich sind. Dann erhält man für eine beliebige, auf die ganze Spannweite gleichmäßig verteilte Last von u pro Längeneinheit die Beanspruchungen der Stäbe (Zug positiv, Druck negativ) im m ten Felde der ersten Trägerhälfte von Fig. 1 und symmetrisch dazu:
[101] Für den ersten Untergurtstab und die mittlere Vertikale jedoch gelten ausnahmsweise:
Im Falle von Fig. 1 werden also die Diagonalen gedrückt, die Vertikalen gezogen. – Die Beanspruchungen der Stäbe auf der ersten Trägerhälfte von Fig. 2 und symmetrisch dazu ergeben lieh bei den dortigen Bezeichnungen im gleichen Belastungsfälle wie oben:
jedoch ausnahmsweise für den ersten Obergurtstab und die mittlere Vertikale:
Im jetzigen Falle werden also die Diagonalen gezogen, die Vertikalen, mit Ausnahme der mittleren, gedrückt. – Für den Träger (Fig. 3) schließlich sind die Stabkräfte bei der angenommenen Belastung:
und wieder ausnahmsweise Z1 = Z2. Die Stützenreaktionen sind in den beiden ersten Fällen:
im letzten Falle, neben Xn:
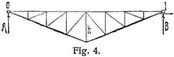
Wird sowohl das Eigengewicht als die Verkehrslast (letztere bei Dachbindern Schneedruck und, wenn kein schiefer Winddruck berücksichtigt wird, auch der Vertikaldruck des Windes) als gleichmäßig verteilt auf die Spannweite bezw. auf die ergriffene Strecke betrachtet, und bezeichnen g, p die entsprechenden Belastungen pro Längeneinheit, so ergeben sich die oberen Grenzwerte der Stabkräfte und Stützenreaktionen aus vorstehenden Gleichungen mit u = g + p = q, die unteren mit u = g, wonach letztere zu ersteren im Verhältnis g: q stehen. Beim Ansatze obiger Gleichungen ist angenommen, daß die ganze Belastung u in den Knotenpunkten des Obergurts angreift. Kommt ein Teil gu von u auf die Knotenpunkte des Untergurts, dann ist sämtlichen Ausdrücken von Vm, Vσ je gu λ zu addieren, während die Beanspruchungen der Gurtungen und Diagonalen ungeändert bleiben. – Ableitung obiger Formeln s. [1], 38, 39, und [2], S. 228, 230, Beispiele der Berechnung nach denselben [2], B 49, 50, Berücksichtigung schiefen Winddrucks [2], B 22. Formeln für beliebige Belastung in den Fällen Fig. 1 und 2 s. [1], §§ 38–40, im Falle Fig. 3 [2], A 20, 26. Berechnung von Dreieckträgern als Brückenträger, z.B. nach der Anordnung Fig. 4, s. [1], §§ 39, 40, Beispiel hierzu für gleichmäßig verteilte bewegte Last [2], B 51, für bewegte Radlastzüge 12], B 52. – Bei horizontalem Untergurt wird auch der Polonceau-Träger (s.d.) oder Wiegmann-Träger zu einem Dreieckträger. Literatur: [1] Weyrauch, Theorie der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1887, S. 125. – [2] Ders., Beispiele und Aufgaben zur Berechnung der statisch bestimmten Träger für Brücken und Dächer, Leipzig 1888, S. 227. – [3] v. Ott, Vorträge über Baumechanik, 3. Teil, Prag 1893, S. 252, 296. – [4] Landsberg, Die Statik der Hochbaukonstruktionen (aus dem Handbuch der Architektur), Darmstadt 1899, S. 198, 218, 244. – [5] Müller-Breslau, Die neueren Methoden der Festigkeitslehre, Leipzig 1904, S. 21, 25 (statisch unbestimmte Dreieckträger).
Weyrauch.
Buchempfehlung
Jean Paul
Selberlebensbeschreibung
Schon der Titel, der auch damals kein geläufiges Synonym für »Autobiografie« war, zeigt den skurril humorvollen Stil des Autors Jean Paul, der in den letzten Jahren vor seiner Erblindung seine Jugenderinnerungen aufgeschrieben und in drei »Vorlesungen« angeordnet hat. »Ich bin ein Ich« stellt er dabei selbstbewußt fest.
56 Seiten, 3.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Romantische Geschichten III. Sieben Erzählungen
Romantik! Das ist auch – aber eben nicht nur – eine Epoche. Wenn wir heute etwas romantisch finden oder nennen, schwingt darin die Sehnsucht und die Leidenschaft der jungen Autoren, die seit dem Ausklang des 18. Jahrhundert ihre Gefühlswelt gegen die von der Aufklärung geforderte Vernunft verteidigt haben. So sind vor 200 Jahren wundervolle Erzählungen entstanden. Sie handeln von der Suche nach einer verlorengegangenen Welt des Wunderbaren, sind melancholisch oder mythisch oder märchenhaft, jedenfalls aber romantisch - damals wie heute. Nach den erfolgreichen beiden ersten Bänden hat Michael Holzinger sieben weitere Meistererzählungen der Romantik zu einen dritten Band zusammengefasst.
- Ludwig Tieck Peter Lebrecht
- Friedrich de la Motte Fouqué Undine
- Ludwig Achim von Arnim Isabella von Ägypten
- Clemens Brentano Geschichte vom braven Kasperl und dem schönen Annerl
- E. T. A. Hoffmann Das Fräulein von Scuderi
- Joseph von Eichendorff Aus dem Leben eines Taugenichts
- Wilhelm Hauff Phantasien im Bremer Ratskeller
456 Seiten, 16.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum