Gelenkträger [1]
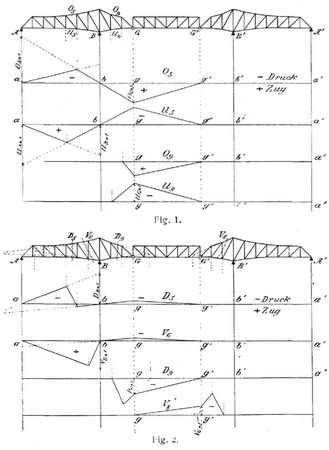
[366] Gelenkträger (graphische Berechnung). Der Mittelteil G G' des in Fig. 1 dargestellten Gelenkträgers ist in statischer Beziehung ein einfaches Fachwerk und nach den für gewöhnliche Fachwerksbalken üblichen Methoden zu berechnen. (Vgl. Parallelträger und Halbparabelträger.) Liegen die Gelenke in den Außenöffnungen, so gilt dasselbe von den beiden Endteilen des Trägers. Es handelt sich daher im folgenden nur um die Berechnung der Träger mit überstehenden Enden A B G und A' B' G'.
Ueber die Belastungsverhältnisse des Gelenkträgers geben die Einflußlinien (s.d.) für die Stabkräfte den deutlichsten Aufschluß; sie bilden das bequemste, wenn auch nicht immer das rascheste Mittel zur Berechnung der Stabkräfte und sind in gewissen Fällen kaum zu entbehren. Ueber die Form und die Art des Verlaufs der Einflußlinien orientiert man sich leicht mit Hilfe der kinematischen Fachwerkstheorie. Denkt man sich nämlich den zu berechnenden Stab allein elastisch und eine Verlängerung Δ s ausführend, die übrigen Stäbe starr, so liefert das Gesetz der virtuellen Verschiebungen S · Δ s = P · m, wobei nur eine einzige Last P angenommen ist, die infolge der Stabverlängerung Δ s die Senkung m erfährt. Mit Δ s = 1 und P = 1 ergibt sich S = m, d.h. die Biegungslinie des Fachwerks infolge der Stabverlängerung gleich eins ist die Einflußlinie der betreffenden Stabkraft. (Vgl. a. Einflußlinien.) Diese Biegungslinie kann man sich leicht vorstellen und es folgen ohne weiteres die in Fig. 1 und 2 gezeichneten Formen der Einflußlinien für die Gurtungs- und Strebenkräfte im Teil A B und im Kragarm B G des Trägers. Verlängert sich z.B. der Obergurtstab O5 um ein kleines Stück, so entsteht im Träger ein nach oben gerichteter Knick am rechten Endpunkt des gegenüberliegenden Untergurtstabs. Zwischen a und b besteht also die Einflußfläche aus einem Dreieck, dessen rechte Seite über b hinaus bis zum Schnitt mit der Senkrechten durch das Gelenk G zu verlängern ist, von wo an die Linie nach g' senkrecht unter dem zweiten Gelenk G' zu ziehen ist. Denn der Fachwerksteil U5 bis G führt bei der gedachten Stabverlängerung eine Drehung um das Auflager B aus, wobei der Geleitpunkt G sich senkt und der angehängte Träger eine geneigte Lage annimmt, indem sein linker Endpunkt G dieser Senkung zu folgen hat, während der rechte Endpunkt G' in Ruhe bleibt.
In ganz ähnlicher Weise ergibt sich die Form der in Fig. 1 gezeichneten Einflußlinie der Stabkraft U5. Durch eine kleine Verlängerung dieses Stabes entsteht im linken Endpunkt von O5 ein nach unten gerichteter Knick und analog dem vorigen der weitere Verlauf der Einflußlinie (als der Biegungslinie) zwischen b und g'. Es ist klar, daß die Einflußlinien zwischen A und B von den auskragenden Enden unabhängig, d.h. ebenso zu konstruieren sind wie für einen einfachen Fachwerksträger von der Spannweite A B. Die beiden Einflußgeraden zwischen a und b schneiden also auf den Auflagersenkrechten durch A und B Strecken ab, die gleich den betreffenden Stabkräften im Belastungszustand A = 1 bezw. B = 1 sind (vgl. Einflußlinien). In Fig. 1 sind diese Kräfte mit OA = 1, UA = 1, UB = 1 bezeichnet. Die negativen Einflußordinaten, die Druck bedeuten, sind nach oben, die positiven, Zugkräfte vorstellenden, nach unten abgetragen. Die Stabkräfte für die Belastungszustände A = 1 bezw. B = 1 können auf verschiedene Weise ermittelt werden, entweder durch Rechnung nach der Ritterschen Momentmethode oder nach dem Culmannschen Schnittverfahren, oder auch mittels eines Cremonaschen Kräfteplans (s.d.) für jeden der beiden Belastungszustände.
Verlängert sich Obergurtstab O9 im Kragarm, so entsteht ein Knick im Gelenk G und eine Drehung um den rechten Endpunkt von U9 und die Biegungslinie und Einflußlinie von O9 erstreckt sich nur von dem letzteren Punkt bis g'. In ähnlicher Weise ergibt sich der Verlauf der Einflußlinie für die Stabkraft U9. Die Höhe dieser Einflußdreiecke oder die Ordinate senkrecht unter dem Gelenk G wird erhalten als Stabkraft für eine in G wirkende Last P= 1, wobei die Ermittlung nach einer der vorhin angegebenen Methoden erfolgen kann.
In Fig. 2 sind die Einflußlinien der Füllungsglieder dargestellt. Bei einer Verlängerung des Diagonalstabs D5 drehen sich die beiden Fachwerksteile der Oeffnung A B gegeneinander[366] um den Schnittpunkt der beiden Gurtstäbe des betreffenden Feldes. Innerhalb des durchschnittenen Feldes verläuft die Einflußlinie geradlinig, hat also die in Fig. 2 gezeichnete Form, wobei sich die von A und B ausgehenden Geraden senkrecht unter dem Schnittpunkt der beiden Gurtstäbe schneiden. Ganz ähnlich ergibt sich der Verlauf der Einflußlinien für V6. Wenn sich D9 um ein kleines Stück verlängert, so bleibt der Schnittpunkt der beiden Gurtstäbe in Ruhe und der links vom Feld liegende Teil dreht sich um diesen Punkt (Momentanzentrum des Gelenkvierecks); von g bis g' muß aber die Einflußlinie gerade verlaufen, und mit dieser Bedingung ergibt sich die in Fig. 2 gezeichnete Form. Aehnlich ergibt sich die Einflußlinie V8', wobei untenliegende Fahrbahn ebenso wie bei V6 vorausgesetzt ist. Bei den Einflußlinien D5 und V6 sind die Abschnitte der von b und a ausgehenden Geraden auf den Auflagersenkrechten durch A und B nichts andres als die entsprechenden Stabkräfte bei den Belastungszuständen A = 1 bezw. B = 1, und für die Stabkräfte D9 und V8 werden die Einflußordinaten unter den Gelenken als die Stabkräfte für Einzelbelastung P = 1 in den Gelenken G bezw. G' zu berechnen sein.
Selbstverständlich könnte man die Stabkräfte auch aus den Einflußlinien der zugehörigen Schnittmomente bestimmen. Dieselben haben einen ähnlichen Verlauf, und die daraus gefundenen Grenzwerte wären jeweils durch den Hebelarm der Stabkräfte in bezug auf ihren Momentendrehpunkt zu dividieren. – Will man den Auflagerdruck A (bezw. die Druckkraft im Endpfosten) berechnen, so denkt man sich das Auflager A lotrecht um die Strecke 1 gehoben und zeichnet die daraus entspringende Biegungslinie (Fig. 3). Nach der nämlichen Regel findet man die Einflußlinie für den Auflagerdruck B (Fig. 4).
Die Berechnung der Gelenkträger mittels Einflußlinien besitzt den Vorteil großer Uebersichtlichkeit; legt man mehr Gewicht auf rasche Arbeit, so ist folgender Weg vorzuziehen: Man bestimmt zunächst für das Eigengewicht des Trägers mittels einfacher Rechnungen die Knotenpunktsgewichte und die Auflagerdrücke und zeichnet, darauf gestützt, einen Cremonaschen Kräfteplan (s.d.). In der Fig. 5 ist dieser Plan gezeichnet; er beschränkt sich wiederum auf den Seitenteil des Trägers, da der Mittelteil wie ein gewöhnliches Fachwerk berechnet wird. Der Einfachheit zulieb sind nur die unteren Knotenpunkte als belastet angenommen worden. Die Gurtungskräfte sind an ihrem linken Endpunkt mit der Nummer ihres zugehörigen Momentendrehpunkts bezeichnet. Der Kräfteplan kann für die ständige Belastung auch dann angewendet werden, wenn man die Stabkräfte, die von den Verkehrslasten erzeugt werden, mit Hilfe von Einflußlinien bestimmt. Bei der Bestimmung des Einflusses der zufälligen Last hat man Straßen- und Bahnbrücken zu unterscheiden.
Straßenbrücken: Wie die Einflußlinien der Fig. 1 zeigen, erhalten die Gurtungskräfte des Trägerteils A B ihre Grenzwerte, wenn entweder die Strecke A B oder die Strecke B G' belastet wird. Die Gurtungen des Trägerteils B G werden nur in einem Sinne beansprucht, und zwar am stärksten, wenn die Strecke B G' belastet wird. Aus der Fig. 2 folgt ferner, daß die Strebenkräfte des Trägerteils A B ihren einen Grenzwert erreichen, wenn man den Träger von A bis zur Strebe und von B bis G' belastet, den andern, wenn man den Träger von der Strebe bis B belastet. (Vertikale V6 in Fig. 2 macht hiervon eine Ausnahme, weil sich die zugehörigen Gurtstäbe innerhalb A B schneiden.) Die Strebenkräfte des Trägerteils B G sodann besitzen nur einen Grenzwert, und dieser tritt ein, wenn die Strecke B G' belastet wird. Um sämtliche größten und kleinsten Stabkräfte zu finden, hat man somit dreierlei zu tun: Zuerst berechnet man mittels eines Cremonaschen Planes sämtliche Eigengewichtskräfte. Zweitens berechnet man die Stabkräfte der zufälligen Last für den Trägerteil A B, als ob er ein gewöhnliches einfaches Fachwerk wäre. Die Gurtungskräfte bestimmt man hierbei mittels eines Cremonaschen Planes, die Strebenkräfte mittels des Herzogschen Verfahrens. Drittens belastet man den Trägerteil B G' und zeichnet für diese Belastung einen dritten Cremonaschen Plan; dabei dehnt man diesen Plan auf sämtliche Stäbe von A bis G aus. Schließlich fügt man zu den Eigengewichtskräften die Ergebnisse der zweiten und dritten Berechnung unter gehöriger Berücksichtigung des Vorzeichens hinzu und findet so sämtliche Grenzwerte der Gurtungs- und Strebenkräfte.
Bahnbrücken: Hier verfährt man im allgemeinen wie bei den Straßenbrücken; doch erfordert die Ermittlung der ungünstigsten Laststellungen noch eine besondere Untersuchung. Zunächst werden wiederum die Stabkräfte des Eigengewichts ermittelt. Sodann wird der Trägerteil A B ganz so wie ein einfaches Fachwerk berechnet. (Vgl. Halbparabelträger.) Drittens wird der Einfluß einer von B bis G' reichenden Belastung auf sämtliche Stäbe ermittelt. Handelt es sich hierbei um Stäbe der Strecke A B, so hat man gemäß der in Fig. 3 dargestellten Einflußlinie von A den Lastenzug so zu stellen, daß möglichst viele und große Lasten in die Nähe des [367] Punktes G kommen. Diese Stellung ist identisch mit derjenigen, die in G das größte Biegungsmoment erzeugt, sofern man B G' als einfachen Balken auffaßt. Ist der größte negative Auflagerwiderstand bei A aus seiner Einflußlinie gefunden, so ist von A beginnend ein Cremonascher Kräfteplan für die Strecke A B zu zeichnen. Handelt es sich um Stäbe auf der Strecke B G, so ist für die Gurtungsstäbe (vgl. Fig. 1) die Strecke vom zugehörigen Momentendrehpunkt bis G' so zu belasten, daß in G das größte Moment entsteht, sofern man diese Strecke als einfachen Balken auffaßt; für die Streben dagegen ist der Bahnzug von rechts nach links, die schwersten Lasten voran, so weit vorzuschieben, bis die erste Last über dem nächsten Knotenpunkt rechts vom durchschnittenen Feld steht. Zur Bestimmung der Stabkräfte können auch hier Kraft- und Seilecke verwendet werden, doch ist dieses Verfahren ziemlich umständlich und wenig übersichtlich, so daß es sich für diesen Fall besser empfiehlt, mit Einflußlinien zu arbeiten. Schließlich werden durch Addition der Eigengewichts- und der zufälligen Stabkräfte unter Berücksichtigung der Vorzeichen die Grenzwerte für sämtliche Stabkräfte gefunden.
Literatur: Ritter, W., Der kontinuierliche Balken, Zürich 1900; Müller-Breslau, Graphische Statik, Bd. 1, Stuttgart 1905.
Mörsch.
Lueger-1904: Gelenkträger, durchlaufender · Gelenkträger [2]
Buchempfehlung
Musset, Alfred de
Gamiani oder zwei tolle Nächte / Rolla
»Fanni war noch jung und unschuldigen Herzens. Ich glaubte daher, sie würde an Gamiani nur mit Entsetzen und Abscheu zurückdenken. Ich überhäufte sie mit Liebe und Zärtlichkeit und erwies ihr verschwenderisch die süßesten und berauschendsten Liebkosungen. Zuweilen tötete ich sie fast in wollüstigen Entzückungen, in der Hoffnung, sie würde fortan von keiner anderen Leidenschaft mehr wissen wollen, als von jener natürlichen, die die beiden Geschlechter in den Wonnen der Sinne und der Seele vereint. Aber ach! ich täuschte mich. Fannis Phantasie war geweckt worden – und zur Höhe dieser Phantasie vermochten alle unsere Liebesfreuden sich nicht zu erheben. Nichts kam in Fannis Augen den Verzückungen ihrer Freundin gleich. Unsere glorreichsten Liebestaten schienen ihr kalte Liebkosungen im Vergleich mit den wilden Rasereien, die sie in jener verhängnisvollen Nacht kennen gelernt hatte.«
72 Seiten, 4.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Geschichten aus dem Sturm und Drang. Sechs Erzählungen
Zwischen 1765 und 1785 geht ein Ruck durch die deutsche Literatur. Sehr junge Autoren lehnen sich auf gegen den belehrenden Charakter der - die damalige Geisteskultur beherrschenden - Aufklärung. Mit Fantasie und Gemütskraft stürmen und drängen sie gegen die Moralvorstellungen des Feudalsystems, setzen Gefühl vor Verstand und fordern die Selbstständigkeit des Originalgenies. Michael Holzinger hat sechs eindrucksvolle Erzählungen von wütenden, jungen Männern des 18. Jahrhunderts ausgewählt.
- Jakob Michael Reinhold Lenz Zerbin oder Die neuere Philosophie
- Johann Karl Wezel Silvans Bibliothek oder die gelehrten Abenteuer
- Karl Philipp Moritz Andreas Hartknopf. Eine Allegorie
- Friedrich Schiller Der Geisterseher
- Johann Wolfgang Goethe Die Leiden des jungen Werther
- Friedrich Maximilian Klinger Fausts Leben, Taten und Höllenfahrt
468 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum