Online-Bibliothek

Gewölbe [1]

[498] Gewölbe, Steindecken, aus einzelnen natürlichen oder künstlichen Steinen so zusammengefügt, daß sie vermöge der Gestalt und Lage dieser Steine durch[498] die Umfassungsmauern des zu überdeckenden Raumes oder durch Stützen (Säulen) schwebend im Gleichgewicht erhalten werden und außerdem imstande sind, entsprechende Lasten zu tragen. Der Eigenart des Gewölbes entspricht die Keilform der Steine, die sich aus der Richtung des in jedem Punkte eines Gewölbes herrschenden Druckes ergibt (s. Drucklinie). Daher sind Gewölbe aus Bruchsteinen und Gußgewölbe (s.d.), bei welchen nur durch das Abbinden des i Mörtels eine zusammenhängende, gebogene oder ausgehöhlte Platte gebildet wird, nicht Gewölbe im eigentlichen Sinne, sondern gehören nur zu der allgemeinen Gattung der Steindecken.

Die Kunst des Gewölbebaues aus keilförmigen Steinen ist nach den neueren Forschungen [7], S. 121, [8], S. 46, eine sehr alte, wie sich dies aus den Ueberresten von Kanälen, Toren, Brücken u.s.w. in Babylon, an verschiedenen Orten Assyriens u.s.w. erwiesen hat; jedoch erst die Römer haben den Gewölbebau zu richtiger Entwicklung gebracht und ihn bei ihren Tempel- und Palastbauten in staunenswerter Weise verwendet. Sodann war es die in den Dienst der Kirche tretende Baukunst, die bei den byzantinischen, romanischen und gotischen Kirchenbauten weitere Fortschritte des Gewölbebaues bezüglich geringerer Massenbildung und verschiedenartiger Formgebung herbeiführte, während in neuerer Zeit bei der Ueberdeckung größerer Räume der Stein durch das Eisen vielfach zurückgedrängt wird und nur der Brückenbau, namentlich bezüglich weiterer Ausbildung der Theorie des Gewölbebaues, Fortschritte aufzuweisen hat.

I. Gewölbeteile und Gewölbeformen.

Da sich alle Gewölbeformen geometrisch sowohl, als auch bezüglich des Steinschnitts und des Steinverbandes auf das zylindrische oder Tonnengewölbe zurückführen bezw. aus diesem ableiten lassen, so ist als Urform der Gewölbe das Tonnengewölbe anzusehen und sind auch die Bezeichnungen seiner einzelnen Teile auf die entsprechenden der übrigen Gewölbe übertragen bezw. ihnen angepaßt worden.

a) Gewölbeteile. Man unterscheidet beim Tonnengewölbe (s. Fig. 1): 1. die Widerlagsmauern oder Widerlager W, gegen welche das Gewölbe sich stützt und auf welche es einen gewissen Schub ausübt; 2. die Stirnmauern oder Schildmauern S, welche das Gewölbe seitlich abschließen und keinem Schübe ausgesetzt sind; sind keine Stirnmauern vorhanden, so wird das Haupt oder die Stirn H des Gewölbes sichtbar und das Gewölbe wird zu einem offenen; 3. die Laibung L, welche die innere oder untere Begrenzungsfläche des Gewölbes bildet; 4. den Rücken R als obere oder äußere Begrenzungsfläche; 5. die zwischen dem Rücken und den weiter hinausgeführten Widerlagsmauern befindlichen Räume, welche Zwickel oder Gewölbezwickel genannt werden; 6. die zur Laibung als ihr lotrechter Schnitt in einer gewissen Beziehung stehende Wölblinie, Wölbungslinie oder Bogenlinie abc, durch deren Form auch die Gestalt der Laibungsfläche bestimmt wird. Ihre Endpunkte a und c, deren Entfernung voneinander die Gewölbeweite oder Spannweite festsetzt, heißen Kämpferpunkte, ihr Mittelpunkt M bestimmt die Lage der Achse des Gewölbes und ihr Scheitelpunkt b ergibt durch seinen Abstand von der Verbindungslinie a c der Kämpferpunkte die Gewölbehöhe oder Pfeilhöhe f des Gewölbes; 7. die Verbindungslinie der auf ein und derselben Seite des Gewölbes liegenden Kämpferpunkte heißt Kämpferlinie (in Fig. 1 a d und die zu a d Parallele von c aus) und die durch die beiden Kämpferlinien festgesetzte Ebene Kämpferebene; 8. die aufeinander folgenden Lagen der Scheitelpunkte legen die Scheitellinie des Gewölbes fest; 9. die rechts und links von einer durch die Scheitellinie gelegten lotrechten Ebene befindlichen Gewölbeteile werden Gewölbeschenkel genannt; 10. Kämpfersteine oder Anfänger, auch Gewölbeanfang oder Gewölbefuß genannt, sind die unmittelbar auf dem. Widerlager ruhenden Gewölbesteine A, während ihre durch a m und c n bestimmte Auflagerfläche die Gewölbesohle oder Widerlagsfläche heißt; 11. der in einem Gewölbequerschnitt am höchsten gelegene, die Scheitellinie enthaltende Gewölbestein B wird der Schlußstein genannt; seine Höhe in der Mitte bestimmt die Scheitelstärke des Gewölbes, während an jeder andern Stelle die Länge der an der Gewölbestirn oder, wenn diese schief ist, die Länge der im zur Gewölbeachse senkrechten Schnitt sichtbar werdenden, senkrecht zur Wölblinie gerichteten Gewölbefuge als Maß für die Gewölbedicke oder Gewölbestärke gilt; 12. Gewölbescharen oder Gewölbeschichten sind die in gleicher Höhe liegenden Steinreihen, welche von je zwei benachbarten Lagerflächen begrenzt sind. Durch die Stoßflächen werden ferner die Gewölbeschichten in einzelne Gewölbesteine geteilt.

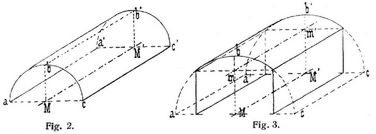
b) Gewölbeformen. Die Gestalt der Laibungsfläche eines Gewölbes ist maßgebend für die Steinanordnung sowohl wie für seine Benennung, und auf einfach synthetisch-geometrischem Wege lassen sich aus der Urform der Gewölbe, aus dem Tonnengewölbe, die Formen der Laibungsflächen der übrigen Gewölbearten ableiten. Die einfachste Form der Laibungsfläche[499] eines Tonnengewölbes ist die durch geradlinige Fortbewegung eines halbkreisförmigen Bogens abc entstehende Mantelfläche eines halben geraden Kreiszylinders (s. Fig. 2); die Achse des Gewölbes MM' wird hier durch die Fortbewegung des Mittelpunktes M des halbkreisförmigen Bogens erzeugt und steht senkrecht zu den Stirnflächen, so wie jeder senkrecht zur Achse geführte Schnitt a' b' c' einen Halbkreis als Wölblinie ergibt. Die Kämpfer- und Scheitellinien a a', c c' bezw. b b' liegen wagerecht und sind parallel zur Achse, während die Pfeilhöhe M b der halben Spannweite gleich ist. Verändert sich die Form der Wölblinie, indem sie weniger als die Hälfte der Spannweite zur Pfeilhöhe erhält, so entsteht das flache oder Stichbogengewölbe (vgl. Fig. 3), welches auch Kappengewölbe oder preußische Kappe genannt wird, wenn das Pfeilverhältnis 1 : 10 bis 1 : 12 wird. Besteht die Wölblinie aus einer halben Ellipse, einer Parabel oder einem Korbbogen, so entsteht ein elliptisches bezw. parabolisches oder Korbbogengewölbe. Dabei können, je nachdem die Pfeilhöhe kleiner oder größer als die halbe Spannweite angenommen wird, gedrückte bezw. überhöhte Gewölbe unterschieden werden.

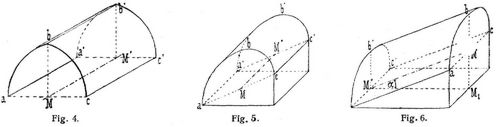
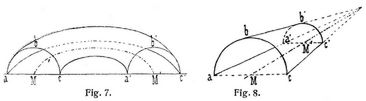
Ist die Wölblinie eine gerade Linie oder ein Kreisbogen mit unendlich fernem Mittelpunkt, so wird das Gewölbe zum scheitrechten Gewölbe. Bildet die Wölblinie keine stetig gekrümmte Kurve, sondern besteht sie aus zwei Bogenschenkeln, die im Scheitel einen Bogenwinkel bilden, so entsteht ein spitzbogiges oder gotisches Gewölbe (s. Fig. 4). Liegen die Kämpferlinien zwar jede für sich wagerecht, jedoch nicht in ein und derselben Horizontalebene, so heißt das Gewölbe einhüftig (s. Fig. 5), während ein Gewölbe, dessen Kämpferlinien mit der Horizontalebene einen spitzen Winkel α einschließen, ansteigendes Gewölbe (s. Fig. 6) genannt wird. Im Gegensatz zum geraden Gewölbe, dessen Stirnebenen senkrecht zur geradlinigen Achse stehen, heißt ein Gewölbe schief, wenn die Stirnebenen einen spitzen oder stumpfen Winkel mit der Achse einschließen. Bildet die Achse des Gewölbes eine wagerecht liegende, geschlossene oder offene Kurve, so entsteht das Ringgewölbe (s. Fig. 7), und ist die Achse eine Raumkurve, insbesondere eine Schraubenlinie, so wird von der an dieser mit ihrem Mittelpunkt hingleitenden, mit ihrer Ebene stets senkrecht zur Achse bleibenden Wölblinie ein Schneckengewölbe erzeugt. Denkt man sich den beim zylindrischen Tonnengewölbe im Unendlichen befindlichen Schnittpunkt der Zylindererzeugenden ins Endliche gerückt, so entsteht das kegelförmige oder Kegelgewölbe (s. Fig. 8).

Aus der Durchdringung zweier Tonnengewölbe von gleicher Pfeilhöhe entstehen zwei neue Gewölbeformen: das Kreuzgewölbe bezw. das Klostergewölbe, je nachdem man die bei der Durchdringung sich bildenden »Kappen« oder bezw. die »Wangen« oder »Walme« beibehält

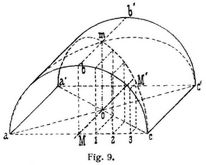
Schneidet man ein halbkreisförmiges Tonnengewölbe (s. Fig. 9) durch zwei lotrechte Diagonalebenen, so entstehen nämlich auf der Laibungsfläche als Schnittlinien dieselben halben Ellipsen, die als Durchdringungskurven sich bilden, wenn ein zweites, gleichgroßes Gewölbe das erstere senkrecht durchdringen würde. Durch diese Schnittlinien oder Durchdringungskurven wird jedes der beiden sich durchdringenden Gewölbe in vier Teile geteilt, von denen je zwei gegenüberliegende einander gleich und symmetrisch gelegen sind. Die Teile a b c m und a' b' c' m werden »Kappen«, die Teile a m' a' und c m c' »Wangen« oder »Walme« genannt. Die Kappen[500] haben nur Kämpferpunkte a und c, a' und c' zu Widerlagern, sind von drei gekrümmten Linien begrenzt und enthalten je einen Teil der Scheitellinie b b' des zerschnittenen Gewölbes. Die Wangen oder Walme dagegen behalten ihr Widerlager und sind von einer Geraden (der Kämpferlinie a a' bezw. c c') und zwei gebogenen Linien begrenzt, die sich im Scheitel des Gewölbes im Punkte m treffen; sie haben also eine Widerlagerlinie und einen Scheitelpunkt. Setzt man nun vier der beschriebenen »Kappen« nach Art der Fig. 10 zusammen, so erhält man die Laibungsfläche eines Kreuzgewölbes über quadratischem Raum, welches vier Widerlagerpunkte und vier Scheitellinien besitzt, von denen je zwei in eine und dieselbe Richtung zusammenfallen, während an den Stellen, an denen sich die Gewölbelaibungen durchdringen, sich nach innen vorspringende Grammen zeigen. Setzt man dagegen vier der vorhin beschriebenen »Wangen« oder »Walme« zusammen, so entsteht die Laibungsfläche eines Klostergewölbes über quadratischem Raum, bei welchem die vier Umfassungsmauern Widerlagermauern bilden, während die Spitzen der Wangen in einem Punkte m (s. Fig. 11) zusammentreffen, wo auch ihre einspringenden Grammen als Durchdringungslinien der Laibungsflächen zusammenlaufen.

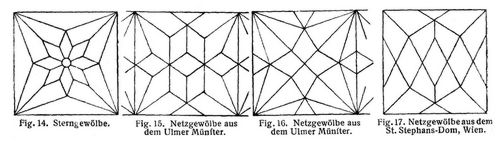
Der Grundriß des mit einem der beiden genannten Gewölbearten zu überdeckenden Raumes braucht jedoch keineswegs quadratisch zu sein, sondern kann beliebig, regelmäßig oder unregelmäßig polygonal gestaltet werden. Man erhält über demselben ein Kreuzgewölbe, wenn man die Ecken der polygonalen Grundrißfigur als Widerlagerpunkte ebensovieler Kappen von gleicher Pfeilhöhe anfleht (s. Fig. 12), die mit ihren Spitzen sich in einem Punkte, dem Schnittpunkt der Scheitellinien, vereinigen, während bei der Bildung eines Klostergewölbes die Seiten der polygonalen Grundrißfigur zu Kämpferlinien ebensovieler Wangen von gleicher Pfeilhöhe werden (s. Fig. 13), deren Spitzen sich im Scheitelpunkt des Gewölbes treffen. Im Grundriß (vgl. Fig. 12 und 13) zeigt sich in beiden Fällen kein Unterschied; beim Kreuzgewölbe muß die Horizontalprojektion des Schnittpunktes der Scheitellinien, beim Klostergewölbe diejenige des Scheitelpunktes mit dem Schwerpunkt der Grundrißfigur zusammenfallen, und in beiden Fällen werden daher die Horizontalprojektionen der Grammen strahlenförmig nach den Ecken verlaufen. Werden die nach innen vorspringenden, ursprünglich scharfkantigen Grate des Kreuzgewölbes als profilierte Rippen ausgebildet, so entsteht das gerippte Kreuzgewölbe, und wird die Zahl dieser Rippen vermehrt, so daß der Grundriß stern- und netzförmige Figuren bildet (vgl. Fig. 14–17), so erhält man die Laibungsflächen des Stern- bezw. Netzgewölbes.

Durch unendliche Vermehrung der in einem Widerlagerpunkt zusammenlaufenden Rippen des Sterngewölbes oder durch Umdrehung der halben Wölblinien der Kreuzkappen um die in den Widerlagerpunkten gedachten Lotlinien als Achsen erhält man die Laibungsfläche des Fächer- oder Trichtergewölbes, das auch normännisches oder angelsächsisches Gewölbe genannt wird.

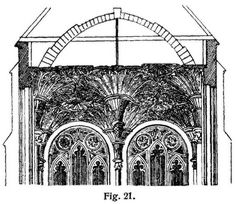
Das Fächer- oder Trichtergewölbe zeigt auf seiner Laibungsfläche Umdrehungsflächen, die im Scheitel zum Teil aneinander flößen, zum Teil durch zwischengeschaltete Uebergangsflächen[501] miteinander verbunden werden. Bei quadratischem Grundriß erhält man ein solches Gewölbe, wenn man (s. Fig. 18) in jeder der vier Ecken einen Viertelkreis oder eine andre Wölblinie um eine lotrechte Achse um 90° sich gedreht denkt und die durch die Bewegung – bei welcher jeder Punkt der Wölblinie wagerecht liegende Viertelkreise beschreibt – erzeugte trichterförmige Fläche als Laibungsfläche eines Gewölbes anfleht, in dessen Scheitel eine von vier konvexen Viertelkreisen a a₁, a₁ a₂, a₂ a₃ und a₃ a begrenzte Oeffnung a a₁ a₂ a₃ frei bleibt, die durch ein scheitrechtes Gewölbe geschlossen werden kann. Häufig wurde diese Oeffnung mit vortretenden Rippen gesäumt und durch einen die vier Viertelkreise berührenden Kreis geteilt, der durch eine vor die Laibungsfläche vortretende, die trichterförmigen Flächen verspannende Rippe ausgezeichnet und durch eine flache Kuppel überwölbt wurde, während die vier Zwickelfelder ebenfalls flache Ueberwölbungen erhielten (s. Fig. 19). Statt die trichterförmigen Flächen durch die Viertelkreise a a₁, a₁ a₂ u.s.w. zu begrenzen, kann man sie, der Wölblinie entsprechend, auch weiter fortgesetzt denken, so daß sie sich durchdringen und dadurch eigenartig gekrümmte Grammen entstehen, wie dies Fig. 20 für einen länglich rechteckigen Grundriß zeigt, wobei die nachträglich einzuwölbende Oeffnung fortfällt und keine weiteren Zwischenflächen eingewölbt zu werden brauchen. Diese Art der Trichtergewölbe eignet sich besonders für die Ausführung in Backsteinen, während die zuerst besprochene, namentlich in England bei den mittelalterlichen gotischen Bauten, unter Verwendung des Tudorbogens, zu den verwickeltsten Steinkonstruktionen geführt hat, indem die Trichterfläche in einzelne dem Scheitel zustrebende Rippen mit dazwischengespannten Gewölbefeldern von geringerer Stärke aufgelöst wurde und im Scheitel reichgeformte herabhängende Schlußsteine, die durch besondere Tragbogen im Gleichgewicht gehalten werden mußten, zur Verwendung kamen (s. Fig. 21) [7], S. 190. Auch wurde vielfach die von den sich berührenden Trichterflächen offen gelassene Scheitelfläche mit einem reichen Maßwerk netzförmig ausgefüllt. In späterer Zeit wurde das verzierende reiche Rippenwerk in England erst nach hergestellter Ueberwölbung in die Gewölbelaibung eingemeißelt und verlor somit den konstruktiven Charakter. In gleicher Weise kann bei in Backsteinen ausgeführten Gewölben durch Stuck und Malerei das Rippen- und Maßwerk in phantastischster Form hergestellt werden. Bei Verwendung des Trichtergewölbes für größere Räume muß ihr Grundriß durch Säulenstellung in Rechtecke oder Quadrate geteilt werden, wobei in jeder Ecke Vierteltrichter, an den Wänden halbe und über den Säulen ganze Trichter entstehen (s. Fig. 22). Beispiele neuerer Ausführungen sind die unter Leitung von Persius ausgeführte Decke des Bibliothekzimmers im Schlösse zu Babelsberg [7], S. 189, und die Decke der von Schlüter erbauten Börsenhalle zu Frankfurt a.M. [7], S. 188. Auch in der von Oberbaurat v. Leins erbauten Königsvilla in Berg bei Stuttgart sind Ueberwölbungen mit Trichtergewölben ausgeführt worden [7], S. 188. Vgl. a. [1], [2], S. 458, [3], S. 178, [4], S. 67, [7], S. 187, [9], S. 495.

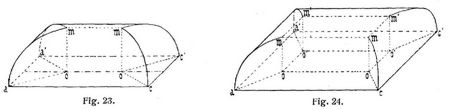
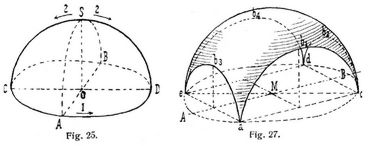
Als Abarten des Klostergewölbes können das Muldengewölbe (s. Fig. 23) und das Spiegelgewölbe (s. Fig. 24) angesehen werden. Die Laibungsfläche des ersteren entsteht. wenn ein Tonnengewölbe an den Enden mit entsprechenden Wangen abgeschlossen wird[502] (s. Fig. 23); letzteres wird gebildet, wenn ein scheitrechtes Gewölbe rings mit Wangenstücken umgeben wird (s. Fig. 24). Wird die Anzahl der Seiten der Grundrißfigur eines Klostergewölbes unendlich groß, so geht es in das Kuppelgewölbe über, das infolgedessen eine in sich selbst geschlossene krumme Linie als Kämpferlinie besitzt und, da die Grammen verschwinden, eine einheitlich gekrümmte, zusammenhängende Laibungsfläche aufweist (Fig. 25). Wird als Grundrißform des zu überwölbenden Raumes der Kreis angenommen, so erhält man in allen lotrecht durch den Scheitelpunkt gelegten Querschnitten lauter kongruente Kurven (Meridianlinien); sind diese insbesondere kongruente Kreisabschnitte, so ist das Gewölbe ein Kugelgewölbe.

Unter Voraussetzung eines Kreises als Grundrißfigur kann die Laibungsfläche des Kuppelgewölbes daher auch ganz allgemein als Umdrehungsfläche angesehen werden, die durch Umdrehung eines Viertelmeridians A S (Viertelkreis, Viertelellipse, Parabel, Korblinie u.s.w., s. Fig. 25) um die lotrechte Achse O S in der Pfeilrichtung 1 erzeugt wird und je nach der zugrunde gelegten Erzeugungskurve die Laibungsfläche eines kugelförmigen, elliptischen u.s.w. Kuppelgewölbes darstellen wird. Anderseits kann, unter Voraussetzung der Kongruenz der Meridianlinie A S B (über der einen Achse A B der Grundrißfigur) mit der halben Grundrißlinie (A D B bezw. A C B), die Erzeugung der Kuppellaibung auch durch Bewegung der Meridianlinie A S B in der Pfeilrichtung 2 (s. Fig. 25) nach der einen und andern Richtung entstanden gedacht werden.

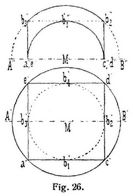
Bei Kuppelgewölben über rechteckigen Räumen können sich verschiedene Anordnungen ergeben. Ist der Kuppeldurchmesser gleich der Diagonale der zu überwölbenden quadratischen oder rechteckigen Grundrißfigur (s. Fig. 26 und 27), so ergibt der Diagonalschnitt über e c eine Meridiankurve, während die Seitenflächen des zu überwölbenden Raumes kleinere Kurven aus der Laibungsfläche herausschneiden, welche den Charakter von Schildbogen (s.d.) tragen, hier aber als Kämpferlinien anzusehen sind. Da ein solches Gewölbe in den Ecken des Raumes gewissermaßen tiefer herabhängt, nennt man es eine Hängekuppel. Ist bei halbkugelförmiger Kuppel der zu überwölbende rechteckige Raum insbesondere quadratisch, so werden die Schildbogen zu untereinander kongruenten Halbkreisen (s. Fig. 26), während bei länglich rechteckigem Grundriß nur die gegenüber liegenden Schildbogen kongruente Halbkreise sind (s. Fig. 27). In beiden Fällen lassen sich die Umfassungsmauern halbkreisförmig durchbrechen, so daß dann eine nur auf vier in den Ecken angebrachten, durch Mauerbogen zu verbindenden Stützen (Pfeilern, Säulen) aufruhende Hängekuppel entsteht. Wird der Kugeldurchmesser größer als die Diagonale der rechteckigen Grundrißfigur, so entsteht eine flache Hängekuppel, die den Namen böhmisches Gewölbe oder böhmisches Kappengewölbe führt, das auch über beliebig polygonalem Raum errichtet gedacht werden kann, wenn die Horizontalprojektion des Kugelmittelpunktes mit derjenigen des Schwerpunktes der Grundrißfigur zusammenfallend angenommen wird.

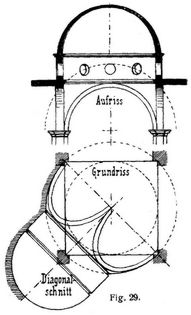
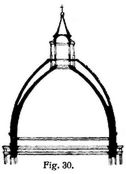
Ist der Kuppeldurchmesser kleiner als die Diagonale des Rechtecks, so entsteht ein zusammengesetztes Kuppelgewölbe, das ebenfalls »Hängekuppel« genannt wird und aus den in die Ecken hinabreichenden Teilen (den »Gewölbezwickeln«) der einfachen Hängekuppel und der auf ersteren mittels eines meist durch ein Kranzgesims hervorgehobenen Ringes aufruhenden eigentlichen Kuppel besteht (s. Fig. 28); wird zwischen der letzteren und den Gewölbezwickeln ein Zylinderstück (Trommel, Tambour) eingeschaltet, so erhält man die Hängekuppel mit [503] Tambour (s. Fig. 29). Wird endlich die häufig zur Beleuchtung des Kuppelraums verwendete, mit einem Licht- oder Schlußring (auch Lichtkranz) versehene obere Oeffnung mit einem Aufsatz, Laterne genannt, versehen, so entsteht das Kuppelgewölbe mit Laterne (Fig. 30). Gleichzeitig zeigt Fig. 30 die Gestalt einer Doppelkuppel, die aus zwei selbständigen Kuppeln mit voneinander unabhängigen Umdrehungsflächen besteht. Wenn von der Laibungsfläche eines Kuppelgewölbes (s. Fig. 25) die Hälfte oder ein größerer Teil abgeschnitten und entfernt wird, so ergibt sich die Laibungsfläche des Nischengewölbes, das bei entsprechender Größe zum Chorgewölbe (s. Chor) wird.

II. Ausführung der Gewölbe.

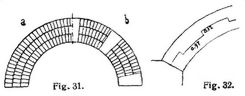
Ebenso wie die Gewölbeformen sich aus der Urform des Tonnengewölbes ableiten lassen, kann auch die Einwölbungsweise aller Gewölbe auf diejenige des Tonnengewölbes zurückgeführt werden. In allen Fällen ist man bestrebt, die Lagerflächen möglichst senkrecht zur Druckrichtung zu Hellen, woraus sich für das Tonnengewölbe auf die ganze Tiefe des Gewölbes durchlaufende keilförmige Schichten oder »Scharen« und parallel zu den Kämpferlinien verlaufende Lagerfugen ergeben (Einwölbung »auf den Kuf«). Nur mit wenigen Ausnahmen (beim Kappen-, Kreuz- und Kuppelgewölbe, s. unten) ist stets während der Ausführung der Gewölbe ein Lehrgerüst (s.d.) zur Unterstützung der Wölbsteine erforderlich. Auf der Einschalung eines solchen Lehrgerüstes erfolgt dann die Einwölbung symmetrisch gegen den Scheitel, dessen Lage auf den Lehrbogen oder auf der Schalung bezeichnet sein muß. An den Kämpfern muß, wegen der ungeraden Teilung der Wölblinie, mit der gleichen der zwei abwechselnd sich überbindenden Schichten begonnen werden. Zur Nachprüfung der richtigen Stellung der Lagerflächen kann bei Mauerbogen (s.d.) und an der Stirn offener Gewölbe mit kreisförmiger Wölblinie eine Schnur benutzt werden, die mit einem Nagel im zugehörigen Mittelpunkt an einer geeignet angebrachten Latte oder dergl. befestigt wird. Kann der Mittelpunkt nicht in dieser Weise erreicht werden oder hat man es mit einem an den Stirnen geschlossenen Gewölbe zu tun, so wird eine Schablone hergestellt, die, auf die Einschalung gestellt, durch ihre Seitenkante die jedesmalige Richtung der Fuge angibt. Der Schlußstein bezw. die Schlußschicht muß vorsichtig eingesetzt werden, damit das Gewölbe nicht erschüttert wird. Zu, empfehlen ist es, besonders bei Hausteineinwölbungen, den Schlußstein trocken einzusetzen und die Fugen von oben auszugießen. Nach Einsetzen des Schlußsteins wartet man die Erhärtung des Mörtels ab, worauf die Lehrgerüste vorsichtig ausgerüstet werden können (s. Ausrüsten). Bei den Mauerbogen aus Werksteinen reichen gewöhnlich die keilförmigen Wölbsteine durch die ganze Mauer. Bei Gewölben aus Werksteinen ist darauf zu achten, daß die Lagerflächen der einzelnen Wölbsteine einer Schicht in einer Ebene durch das ganze Gewölbe hindurchgehen, also in einer Schicht nur Steine von gleicher Dicke liegen. Obgleich bei Werksteinen der Mörtel mehr die Aufgabe gleichmäßiger Druckverteilung übernimmt, weshalb häufig nur dünne Lagen aus Weißkalk oder Bleiplatten verwendet werden, scheint die Mörtelverbindung doch gut zu gelingen, wenn man nach Rheinhard [11], [12] sehr steifen Mörtel verwendet und ihn in sehr weite, 15–30 mm starke Fugen der rauh gehaltenen Lagerflächen nach Annässen der Steine von oben einstampft [11], [12], [15], S. 473. Die Wölbsteine werden bei diesem Verfahren auf dem Lehrgerüst im Fugenabstande verteilt und gegeneinander verkeilt. An den Stirnseiten werden die Fugen enger angelegt, und um das Herauspressen des Mörtels zu vermeiden, wird ein Tau eingebracht. Bei Backsteinbogen und Gewölben werden, da keilförmig gebrannte Steine nur selten zur Verwendung kommen (bei profilierten Bogen, im Backsteinrohbau und bei röhrenförmigen Kanälen), infolge der parallelepipedischen Form der Steine die Fugen keilförmig, was bei großen Gewölbestärken dazu geführt hat, statt durch die ganze Gewölbestärke hindurchreichender Schichten (s. Bogenverband) einzelne im Verband gewölbte Ringe übereinander zu setzen (a in Fig. 31). Bei dieser Anordnung wird jeder Ring verschieden beansprucht, also spielt hier die Fertigkeit des Mörtels eine besonders wichtige Rolle. Zu empfehlen ist es, die einzelnen Ringe von Zeit zu Zeit durch Binder miteinander zu verbinden (b in Fig. 31). Auch verzahnte Ringe (Fig. 32) sind von Bräuler [13] in Vorschlag gebracht worden. Bei Bruchsteingewölben kommt es in erster Linie auf guten Mörtel und auf eine gewissenhafte Ausführung an [14]. Sind mehrere Gewölbe nebeneinander einzuwölben und sind die Zwischenstützen als Pfeiler und nicht als Widerlager berechnet, so müssen alle Oeffnungen gleichzeitig eingerüstet oder doch wenigstens abgesteift werden.

a) Tonnengewölbe (Zylindergewölbe). Wird das in seiner Form von der Gestaltung[504] der Wölbungslinie (s.d.) abhängende Tonnengewölbe in der obenbesprochenen Weise mit zu den Kämpferlinien parallelen Lagerfugen eingewölbt, so nennt man es auch Kufgewölbe. Im übrigen sind außer den Mauerbogen (s.d.), die als Tonnengewölbe von geringer Tiefe angesehen werden können, bezüglich ihrer Ausbildung die nachgehenden Arten des Tonnengewölbes zu unterscheiden:

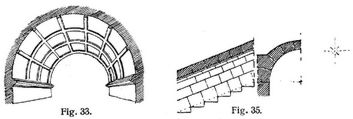
α) Kassettengewölbe oder kassettierte Gewölbe. Kassettengewölbe zeigen auf ihrer Gewölbelaibung eine regelmäßige Gliederung durch umrahmte Vertiefungen (Kassetten). Bei Tonnengewölben aus Backsteinen werden nach einem von Moller angegebenen Verfahren [16] die Querrippen als Ringe und zwischen diesen, sie verspannend, die Längsrippen als scheitrechte Bogen ausgeführt (s. Fig. 33 und 34). Bei der Ausführung werden auf der Verschalung des Lehrgerüstes, entsprechend den Vertiefungen der Kassetten, in regelmäßigen Abständen Holzkasten befestigt, die nach oben etwas verjüngt sind, damit dieselben beim Ausrüsten nicht am Gewölbe hängen bleiben oder Teile desselben mitreißen.

β) Preußische Kappen sind flache Tonnengewölbe mit etwa ¹/_10-¹/₁₂ Pfeilhöhe, die bei Spannweiten bis zu 2,5 m aus Backsteinen in einer gleichmäßigen Stärke von ¹/₂ Stein namentlich zu Kellerüberwölbungen verwendet werden. Die Einwölbung geschieht entweder mit Hilfe von eingeschalten Lehrgerüsten mittels der Kufeinwölbung oder der Mollerschen Einwölbung (s.d.) oder auf Rutschlehrbogen mittels der ringförmigen Einwölbung (s.d.) oder mittels der Schwalbenschwanzeinwölbung (s.d.) mit Hilfe einzelner Lehrbogen.

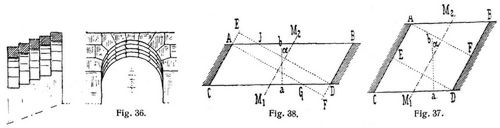
γ) Rampengewölbe oder ansteigende Gewölbe müssen bei Anwendung von Hausteinen einen derartigen Steinschnitt erhalten, daß sowohl das Abrutschen des ganzen Gewölbes auf den Widerlagern als auch das Gleiten der einzelnen Gewölbeschichten verhindert wird [17]. Dies kann durch Abtreppen der Widerlager (s. Fig. 35) oder durch Anwendung von hakenförmig eingreifenden Steinen geschehen. Um diese außergewöhnliche Steinformen bedingende Ausführungsweisen zu umgehen, hat man häufig das Gewölbe in einzelne nebeneinander stehende Bogen aufgelöst (s. Fig. 36, auch Zonengewölbe genannt). Bei Anwendung von Backsteinen hat die Ausführung des Rampengewölbes keine Schwierigkeit, nur muß bei der Einrüstung auf das Bestreben des Abgleitens, solange der Mörtel noch frisch ist, Rücksicht genommen werden.

δ) Schiefe Gewölbe entliehen, wenn die Gewölbeachse M₁ M₂ (s. Fig. 37–41) nicht rechtwinklig zu den Stirnebenen A B bezw. C D gerichtet ist, wobei als Maß der Schiefe der Winkel α gilt, um den die Richtung der Gewölbeachse M₁ M₂ von der Senkrechten a b zur Stirnebene abweicht. Je größer dieser Winkel ist, um so weniger eignet sich die gewöhnliche Kufeinwölbung (s.d.), da bei einer spicken die Kraftübertragung in Ebenen erfolgt, die senkrecht zu den Widerlagerrichtungen stehen, also in Fig. 37 nur der mittlere Teil A F D E standsicher wäre, während die über den dreieckigen Grundflächen A B F und C D E befindlichen Gewölbeteile in den Punkten A bezw. D kein genügendes Auflager fänden, also abgeschert würden, wenn dies nicht etwa durch genügend tief hineinreichende Bindersteine oder durch Verankerung verhindert würde. Bei geringer Gewölbetiefe (s. Fig. 38) könnten auch tief eingreifende Bindersteine das Abscheren nicht mehr verhindern, da hier die lotrechten, senkrecht zu den Widerlagerrichtungen stehenden Ebenen A F und D E das Gewölbe in drei nicht standfähige Teile A, C G, A G D J und D J B zerlegen, von denen der mittlere Teil nur Punktauflager, die beiden Seitenteile A C G und D J B aber in den Punkten G und J gar kein Widerlager besitzen würden. Um die Standsicherheit zu ermöglichen, dürfen daher die von Widerlager zu Widerlager wirkenden Kräfte nicht senkrecht zu den Widerlagerrichtungen hinübergeleitet werden, sondern müssen in Ebenen zur Wirkung gelangen, die parallel zu den Gewölbestirnen liegen. Da nun in jedem Mauerwerk die Lagerflächen senkrecht oder nahezu senkrecht zur Kraftrichtung stehen sollen, so folgt, daß sie auch hier senkrecht zu der soeben angegebenen Richtung zu stellen sind, während die Stoßflächen in diese Richtung selbst fallen, also parallel zu den Gewölbestirnen angeordnet werden müssen. Dieser Grundgedanke hat folgende Lösungen entstehen lassen:[505]

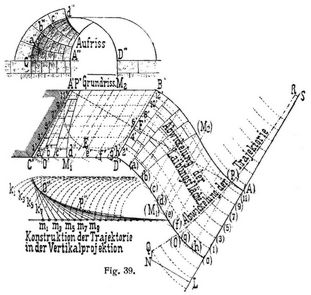
1. Anordnung des orthogonalen, senkrechten oder französischen Fugenschnitts. Hier bilden die Lagerfugen eine Trajektorienschar zu der parallel zur Stirnfläche angenommenen Stoßfugenrichtung. Nach Einteilung der Gewölbestirn C'' a'' b'' c'' D'' (s. Fig. 39) in eine ungerade Anzahl gleicher Teile müßte also von jedem der Teilpunkte a, b c u.s.w. eine Trajektorie zu den Stoßfugenrichtungen 1–2, 3–4 u.s.w. gezeichnet werden. Da aber diese Trajektorien Teile ein und derselben genügend lang gezeichneten Trajektorie sind, so genügt es, die »Scheiteltrajektorie« und ihre Abwicklung zu bestimmen und diese entsprechend zu verschieben. Die Schablone der für die Steineinteilung der abgewickelten Laibungsfläche dienenden abgewickelten Trajektorie kann entweder analytisch ([17] und [18]) oder zeichnerisch bestimmt werden. Fig. 39 zeigt den letzteren Weg für ein schiefes Gewölbe mit einem Halbkreis als Stirnkurve, also einer überhöhten Ellipse A' E F' als Wölblinie. Da die in dem unteren Teil der Fig. 39 herausgezeichneten, im Grundriß den Spuren 1' 2', 3' 4' u.s.w. entsprechenden Stoßfugenrichtungslinien k₁, k₂, k₃ u.s.w. parallel zur Gewölbestirn verlaufen, also in Ebenen liegen, die parallel zur Aufrißebene stehen, so wird jede zu ihnen senkrecht gezeichnete Linie auch in Wirklichkeit senkrecht zu ihnen stehen; somit kann die Trajektorie unmittelbar in der Aufrißebene gezeichnet werden. Verbindet man einen beliebigen, z.B. den dem Stirnkurventeilpunkte b'' entsprechenden Punkt O'', auf k₆ mit dem zugehörigen Mittelpunkt m₆, den Schnittpunkt dieses Halbmessers mit dem Kreise k₇, ferner mit dem Mittelpunkt m₇ u.s.w., so erhält man ein Vieleck, dessen Seiten immer zu dem vorhergehenden Kreise senkrecht stehen, die nachfolgenden Kreise dagegen unter einem spitzen Winkel schneiden. Verbindet man hingegen O'' auf k₆ mit m₇, den Schnittpunkt dieser Linie mit dem Kreise k₇, dann mit m₈ u.s.w., so ergibt dieses ein Vieleck, dessen Seiten zu den nachfolgenden Kreisen senkrecht stehen, die vorhergehenden dagegen unter einem spitzen Winkel schneiden. Denkt man sich die Hilfskreise k₁ k₂ ... u.s.w. ∞ nahe gerückt, so gehen die beiden Vielecke in eine Kurve, d.h. in die gesuchte Trajektorie, über, die im vorliegenden Fall durch Halbieren der Zwischenstrecken als –·– eingezeichnete Kurve gefunden wurde. Wird die auf diese Weise beliebig lang gezeichnete Kurve in die Abwicklung übertragen, so erhält man damit die Schablone L N Q R S, die, längs der Geraden L S verschoben und an die Stirnteilpunkte (h), (g), (f) u.s.w. angelegt, die Lagerfugen auf der Abwicklungsfläche ergibt, wie sie auf der linken Hälfte eingezeichnet sind. Zwischen den Lagerfugen werden die Stoßfugen als Teile der in der Abwicklung als Sinusoiden, im Grundriß als gerade Linien, im Aufriß als Halbkreise erscheinenden Stoßfugenrichtungslinien entsprechend verteilt. Durch die Steineinteilung auf der Abwicklungsfläche, die auch für die Ausführung auf die Verschalung des Lehrgerüstes übertragen werden muß, ist der Steinschnitt des schiefen Gewölbes vollständig bestimmt und kann in gewohnter Weise in die andern Projektionen übertragen werden (s. Fig. 39). Die Lagerflächen werden hier zu Regelflächen, deren Erzeugende stets senkrecht zur Laibungsfläche gerichtet sind, während die Stoßflächen parallel zur Gewölbestirn gerichtete Ebenen sind, welche der Konstruktion nach senkrecht zu den Lagerflächen stehen. Da die Winkel, welche die Scheiteltrajektorie mit den zur Kämpferlinie parallelen Erzeugenden des Zylindergewölbes bilden, stetig abnehmen, werden die Steine einer Schar verschieden breit, und abgesehen von symmetrisch liegenden Steinen, erhalten alle Wölbsteine verschiedene Abmessungen. Auch werden die benachbarten Scharen so schmal, daß je zwei in einen Stirnstein (s. Fig. 39 bei a, b) oder bei größerer Tiefe des Gewölbes in eine neue Schar übergeführt werden müssen. Diese Schwierigkeiten haben zu einer zweiten Lösung, einem Näherungsverfahren, geführt, nämlich zur:

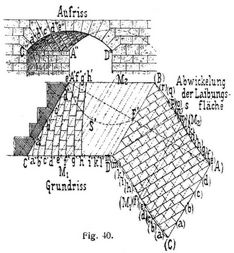
2. Anordnung des angenähert senkrechten oder englischen Fugenschnitts, auch Methode der Schraubenlinien oder des konstanten Fugenwinkels genannt. Hier werden die Trajektorien in der Abwicklung der Laibungsfläche durch gerade Linien ersetzt, die, auf die Laibungsfläche selbst zurückgeführt, Schraubenlinien ergeben (s. Fig. 40), die mit den Zylindererzeugenden a f, b g u.s.w. einen konstanten Winkel einschließen. Nach Zeichnung der Abwicklungsfläche werden die Sehnen B' (A) und D' (C) gezogen. Zu diesen wird in irgendeinem Teilpunkte der Stirnkurve, z.B. im Kämpferpunkte D', eine Senkrechte D' s errichtet. Trifft diese Senkrechte, wie im vorliegenden Fall, auf der andern Seite keinen Teilpunkt, so wird der zunächst liegende Teilpunkt (n) mit D' verbunden. Diese Verbindungslinie ergibt die Richtungslinie, zu der durch die andern Teilpunkte Parallelen (m) (m), (l) (l) u.s.w. gezogen werden. Dadurch erhält man lauter gleichbreite Scharen, die durch zu ihnen senkrecht gerichtete Stoßfugen in gleiche Teile geteilt werden können, so daß, mit Ausnahme der Stirn- und Kämpfersteine, alle Gewölbsteine gleiche Größen erhalten, also auch Backsteine für die innere Laibungsfläche verwendet werden können. Die Lager- und Stoßflächen sind hier Schraubenflächen, deren Erzeugende senkrecht zur Gewölbelaibung stehen. Hat das Gewölbe eine große Tiefe, so kann der mittlere Teil desselben gerade, d.h. »auf den Kuf« (s. Kufeinwölbung), eingewölbt werden, während die Enden, wie Fig. 41 zeigt, entweder nachdem soeben besprochenen englischen Fugenschnitt (rechte Seite der Abwicklung in Fig. 41)[506] oder nach der unter 3. erörterten »orthogonal-konvergenten Methode« eingewölbt werden (linke Seite der Abwicklung in Fig. 41). In beiden Fällen wird der schiefe Fugenschnitt in entsprechender Weise in den geraden übergeführt.

3. Die orthogonal-konvergente Methode nimmt als Stoßfugenrichtungslinien solche an, deren Ebenen sich in einer lotrecht stehenden Geraden schneiden, deren Spuren also nach einem Punkt O (s. Fig. 41) konvergieren. Die Abwicklung ergibt hier nicht parallele Sinusoiden 1 (1), 2 (2) u.s.w., zu denen in der Abwicklung die Trajektorien (g) (g), (h) (h) u.s.w. einzeln gezeichnet werden müssen. Im übrigen unterscheidet sich diese Methode nicht von der orthogonalen. Die Länge des kürzeren Widerlagers vom schief eingewölbten Gewölbeende wird mindestens der halben Spannweite gleich gemacht, so daß sich aus dieser Beziehung die Anwendbarkeit der verschiedenartigen Einwölbungsweise für die Gewölbeenden und den mittleren Gewölbeteil ergibt.

4. Die Zerlegung des Gewölbes in einzelne schmale, gerade eingewölbte Streifen führt zum Zonengewölbe (s.d.).

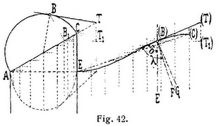
5. Grenzen der Anwendbarkeit. Es ist bei den verschiedenen Ausführungsweisen darauf zu achten, daß namentlich in der Gegend der Bruchfuge die Ecken und Kanten der Steine nicht zu spitz ausfallen. Bezeichnet B in Fig. 42 die Lage der Bruchfuge (s.d.) in der Umlegung der Stirnkurve, so ist in der Abwicklung die Richtung der Lagerfuge für diesen Punkt für die verschiedenen Ausführungsweisen bestimmt durch: 1. die Senkrechte (B) G zur Tangente (B) (T) in (B) für die »orthogonale« Methode; 2. die Senkrechte (B) F zur Sehne E (C) für die »englische« Methode; 3. die Parallele (B) E zur Kämpferlinie für die »gerade« Einwölbung. Solange der Winkel δ > 80°, kann noch »gerade« eingewölbt werden; ist der Winkel λ > 80°, so kann die »englische« Methode zur Anwendung kommen, und erst wenn Winkel λ < 80°, ist es gut, sich der »orthogonalen« Einwölbung zu bedienen. Dies gilt insbesondere für den Halbkreis und den Korbbogen als Wölblinie, während für den Stichbogen stets, wenn nicht mehr gerade eingewölbt werden kann, die »englische« Methode den Vorzug verdient.

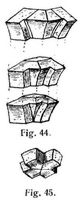
b) Kreuzgewölbe sind mit wagerechten Scheitellinien nur in Hausteinen ausführbar. Die Einwölbung erfolgt dabei stets »auf den Kuf«, d.h. mit parallel zu den Achsen der Kappen liegenden Schichten (s. Fig. 43) auf vollständig eingeschaltem Lehrgerüst. Die Gratsteine greifen in diesem Fall in je zwei benachbarte Kappen und haben ebenso wie die Kämpfersteine und der Schlußstein eine besondere Form; der letztere wird kreuzförmig (s. Fig. 44 und 45). Bei Ausführungen in Backsteinen (s. Fig. 46–49) läßt man in der Regel die Scheitellinien der Kappen[507] nach der Mitte zu etwas ansteigen (mit einem Pfeil von etwa 0,025 im Verhältnis zur Diagonale), weil sonst durch die stets erfolgende, wenn auch geringe Senkung des Scheitels nach dem Ausrüsten der letztere tiefer als die höchsten Punkte der Schildbogen zu liegen käme (s. Stechen der Gewölbe). Man wendet hier am bellen den »Schwalbenschwanz«-Verband an, bei dem die Lagerflächen senkrecht zur Gratbogenlinie gerichtet sind und die einzelnen Schichten in den Scheitellinien der Kappen grätenförmig übereinander greifen. Dadurch sowie durch die Neigung der Kappen gegen die Schildmauern wird ein Teil des Gewölbeschubes auf die letzteren oder auf die Gurtbogen übertragen, und die Stelle im Grat, der meist nach Fig. 46 und 47 noch eine Verstärkung erhält, wird für den Backsteinverband konstruktiv einfacher als bei der Kufwölbung. Es braucht bei dieser Einwölbungsweise auch kein vollständiges Lehrgerüst errichtet zu werden; die Aufstellung einiger Lehrbogen genügt. Erhalten die Schildbogen ungleiche Pfeilhöhen, so kommen auch gekrümmte Scheitellinien zur Anwendung (s. Fig. 48), wodurch die Kreuzkappen »busig« oder »busenförmig« werden. Dies ist vielfach der Fall bei den gotischen Kreuzgewölben, und zwar unterscheidet man hier: 1. gleichhoch mit dem Scheitel liegende Schildbogenscheitel (s. Fig. 50), 2. tiefer als der Gewölbescheitel liegende Schildbogenscheitel (s. Fig. 49), 3. höher als der Gewölbescheitel liegende Schildbogenscheitel (s. Fig. 51). Bei dem gerippten Kreuzgewölbe bilden die meist aus Hausteinen gewölbten Diagonalrippen und Gurtbogen ein tragendes Gestell, zwischen das die Kappen, meist als ¹/₂ Stein starke Gewölbe, eingewölbt werden (Fig. 52 und 53).

c) Klostergewölbe. Die Einwölbung kann »auf den Kuf« oder »auf den Schwalbenschwanz« erfolgen, und zwar wird ebenso wie bei den Kreuzgewölben bei Klostergewölben aus Hausteinen stets die erstere, bei solchen aus Backsteinen häufig die letztere Einwölbungsweise gewählt. Bei der Einwölbung »auf den Kuf« (s. Fig. 54) bilden die Lagerflächen abgestumpfte Pyramidenflächen und die Schichten oder Scharen geschlossene, vieleckige, der Grundrißfigur ähnliche rahmenartige Figuren. Zur Einwölbung ist eine vollständige Einschalung oder Einlattung erforderlich, und Fig. 55 zeigt die Anordnung der Lehrbogen, von denen zunächst ein ganzer Diagonallehrbogen a a aufgestellt und in der Mitte durch einen Stiel, den sogenannten »Mönch«, unterstützt wird. Gegen diesen Lehrbogen stützen sich zwei halbe Diagonallehrbogen b b, worauf die Hauptbogen c c und die Schiftbogen d d, die beide nach der Wölblinie geformt sein müssen, gestellt und das Ganze eingeschalt oder eingelattet wird. Bei Hausteingewölben sind besondere Gratsteine (s. Stein g in Fig. 54), die in die beiden benachbarten Wangen gehörig eingreifen müssen, und ein Schlußstein S erforderlich. – Bei Backsteineinwölbung muß in den Graten die Stoßfuge der Schar der einen Wange sich genau der Lagerfläche der gleichhohen Schicht der angrenzenden Wange anschließen, weshalb die betreffenden Steine nach einer doppelten Schmiege behauen werden müssen. Für die Schwalbenschwanzeinwölbung genügt die Aufstellung von Lehrbogen allein und kann die Verschalung entbehrt werden. Die Schichten werden in diesem Fall senkrecht zu den Grammen gestellt, so daß sie je in den Mitten der Wangen zusammenstoßen und hier eine sogenannte »Naht« bilden, ähnlich wie bei den auf Schwalbenschwanz eingewölbten Kappen. Wenn die Wangen des Klostergewölbes durch Stichkappen durchbrochen werden, kann eine hübsche Wirkung erzielt werden. Die Abarten des Klostergewölbes, das Mulden- und das Spiegelgewölbe, werden stets auf vollständiger Einrüstung eingewölbt, und zwar ersteres in allen seinen Teilen, letzteres nur in seinen Walmen »auf den Kuf«, während seine wagerechte, zur Aufnahme von Deckengemälden geeignete Spiegelfläche meist schwalbenschwanzförmig eingewölbt wird. Das Espiésche Spiegelgewölbe wird auf vollständiger Einschalung aus einer doppelt und verbandmäßig gelegten Lage von 6–7 cm starken gebrannten Tonplatten hergestellt. Hierzu bedarf es aber eines gut bindenden festen Mörtels, wie ihn in Frankreich der Gips liefert. Zur Ueberdeckung großer Säle, Treppenhäuser u.s.w. wird oft das Spiegelgewölbe verwendet, jedoch in der Weise, daß nur die seitlichen Walme gewölbt oder durch Vorkragen der Schichten gebildet, der mittlere horizontale, den Spiegel bildende Teil dagegen als kassettierte Balkendecke hergestellt wird, wie z.B. im großen Festsaal des Rathauses zu Paris. Häufig wird auch der Spiegel als Oberlicht benutzt. In den beiden letzteren Fällen erscheint die Anwendung einer Eisenkonstruktion zweckmäßig, ueber Räumen mit höchstens 4 m Seitenlänge können bei genügend starken Widerlagsmauern auch Spiegelgewölbe aus Hausteinen hergestellt werden [15], S. 332, und [16], S. 223.

d) Kuppelgewölbe. Der Entstehung aus dem Klostergewölbe mit unendlich schmalen Walmen entsprechend sind hier die Lagerflächen abgestumpfte Kegelflächen, die Lagerfugen geschlossene, der Grundrißfigur entsprechende Kurven, und die Wölbschichten bilden vollständig in sich geschlossene Ringe mit zentral gerichteten, lotrecht stehenden Stoßfugenflächen. Dadurch wird es möglich, die Einwölbung ohne Lehrgerüst vorzunehmen, nur müssen in den einzelnen [508] Schichten, namentlich in denjenigen in höherer Lage, bis sie vollständig geschlossen sind, die Steine vor dem Hinabgleiten bewahrt werden, was bei größeren Kuppeln durch drehbare Lehrbogen, bei kleineren durch Beschweren der einzelnen Steine mittels eines an einer rückwärts befestigten Schnur in den Kuppelraum hinabhängenden Steines erfolgen kann [16], S. 190. Bei Kuppelgewölben mit Kassetten werden diese gewöhnlich nicht bis zum Scheitel hinaufgeführt, sondern es wird in diesem ein sogenannter »Nabel« oder »Spiegel« freigelassen [16], S. 190. Außerdem erfahren die Kassetten in ihrer Höhe und Breite nach dem Scheitel hin eine Verringerung, die nach dem in Fig. 56 angedeuteten Emyschen Verfahren erfolgen kann, indem im Grundriß die Breite eines Kassettenstreifens und eines Steges festgelegt wird und die zwischen die verlängerten Radien o a, o b und o c eingezeichneten Berührungskreise mit den Radien r bezw. R der Kassetteneinteilung im Aufriß zugrunde gelegt werden.

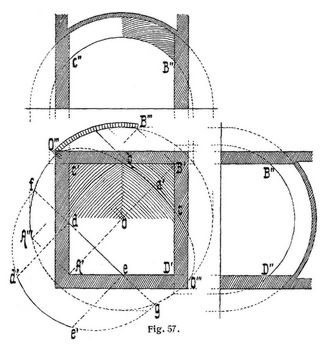
Die Einwölbungsart des böhmischen Kappengewölbes unterscheidet sich von derjenigen des Kuppelgewölbes, da es nicht kufartig in kegelförmigen Ringen, sondern schwalbenschwanzförmig eingewölbt wird, indem die Fugen durch Einteilung des umgelegten Diagonalbogens A''' O''' B''' nach Fig. 57 bestimmt werden. In Wirklichkeit sind demnach auf der Gewölbelaibung die Fugen Teile von größten Kreisen (Meridianbogen) der Kugel, im Aufriß dagegen, ebenso wie im Grundriß, erscheinen sie als Ellipsenteile, wie dies die stärker ausgezogene Fuge b c zeigt, die ein Teil der Ellipse 0''' aO''' ist. Eine beliebige Bogenlinie de erhält man in wahrer Gestalt durch Umklappen des Vertikalschnitts nach dieser Linie durch die Kugel, indem man d e beidseitig bis zu den Schnittpunkten f und g mit dem im Grundriß gezeichneten Aequatorkreise der Kugel verlängert, über f g den Halbkreis f d' e' g schlägt und in den Endpunkten der Horizontalprojektion der Bogenlinie d e die Senkrechten d d' und e e' errichtet; d' e' ist die gewünschte Bogenlinie in wahrer Gestalt. In derselben Weise sind die beiden Vertikalprojektionen C'' B'' und B'' D'', letztere als seitliche Umlegung, wie dies die Fig. 57 durch die punktierten Hilfslinien erkennen läßt, gezeichnet worden. Es sind dies gleichzeitig die Schildbogen des böhmischen Gewölbes. – Als Material wird fast ausnahmslos für diese Art Gewölbe der Backstein benutzt, und zwar geschieht dann die Einwölbung in der Regel aus freier Hand unter Benutzung zweier Diagonallehrbogen und beginnt in den Ecken. Bis zu 5 m Spannweite genügt für die Scheitelstärke ¹/₂ Stein, bis zu 7 m Spannweite ¹/₂ Stein im Scheitel und 1 Stein am Widerlager.

Literatur: [1] Breymann, Konstruktionen in Stein, 1. Teil der Allgem. Baukonstruktionslehre, 5. Aufl., Stuttgart 1879 80. – [2] Wanderley, Die Konstruktionen in Stein, 3. Aufl., Leipzig 1895. – [3] Menzel und Schwatlo, Der Steinbau, Leipzig 1879, S. 277. – [4] Schmölcke, J., Die Konstruktionen des Hochbaues, 1. Teil, Die Gewölbe, Holzminden 1879 – [5] Menzel, CA., Der Gewölbebau etc., herausgegeben von C. Schwatlo, Halle 1866, 2. Aufl. von A.C. Menzel und G. Franke, Halle 1875. – [6] Gottgetreu, R., Beitrag zur geschichtlichen Entwicklung der Gewölbe, Zeitschr. f. Bauw 1879, S. 91. – [7] Gottgetreu, R., Lehrb. d. Hochbaukonstruktionen, 1 Teil, Berlin 1880, S. 121 – [8] Handb. d. Arch., 2. Teil, Bd. 1, Darmstadt 1880, S. 46. – [9] Körner, C., Gewölbte Decken, ebend., 3. Teil, Bd. 2, 3. Heft, Darmstadt 1893 95. – [10] Konstruktion der Gewölbe, Haarmanns Zeitschr. f. Bauhandw. 1876. – [11] Deutsche Bauztg. 1889, S. 142. – [12] Centralblatt d. Bauverw. 1887, S. 325 u. 339. – [13] Ebend. 1890, S. 263. – [14] Vgl. Liebold, Brückenbauten in Zementbruchsteinmauerwerk, Haarmanns Zeitschr. f. Bauhandw. 1882, S. 9. – [15] Handb. d, Arch., Darmstadt, 3. Teil, Bd. 2, 1. Heft, S. 472, und 3. Teil, Bd. 2, 3. Heft, S 217. – [16] Breymann, Baukonstruktionslehre, 6. Aufl., 1. Teil, bearbeitet von O. Warth, Leipzig 1896, S. 158. – [17] Adhémar, Die Lehre vom Steinschnitt, deutsch von Möllinger, Tafel 12, Solothurn 1842, S. 81; Handb. d. Arch., 3. Teil, Bd. 2, 3. Heft, Darmstadt 1893, S. 159. – [18] Annales des ponts et chaussées 1839 S. 1, und 1852, S. 1 – [19] Handb. d. Arch., 3. Teil, Bd. 2, 3. Heft, Darmstadt 1893, S. 166 ff. – [20] Heider, E.J., Theorie der schiefen Gewölbe und deren praktische Ausführung, Wien 1846. – [21] Graeff, Appareil et construction des ponts biais, 2. Aufl., Paris 1867. – [22] Heinzerling Die Brücken der Gegenwart, Steinerne Brücken, 2. Heft, Aachen 1877. – [23] Ders., Grundzüge[509] der konstruktiven Anordnung und statischen Berechnung der Brücken- und Hochbaukonstruktionen, 2. Teil, 2. Heft, Leipzig 1870–74. Sonstige Literatur s. unter Steinschnitt.

L. v. Willmann.

Fig. 1.

Fig. 2., Fig. 3.

Fig. 4., Fig. 5., Fig. 6.

Fig. 7., Fig. 8.

Fig. 9.

Fig. 10., Fig. 11., Fig. 12., Fig. 13.

Fig. 14., Fig. 15., Fig. 16., Fig. 17.

Fig. 18.

Fig. 19.

Fig. 20.

Fig. 21.

Fig. 22.

Fig. 23., Fig. 24.

Fig. 25., Fig. 27.

Fig. 26.

Fig. 28.

Fig. 29.

Fig. 30.

Fig. 31., Fig. 32.

Fig. 33., Fig. 35.

Fig. 34.

Fig. 36., Fig. 37., Fig. 38.

Fig. 39.

Fig. 40.

Fig. 41.

Fig. 42.

Fig. 43.

Fig. 44., Fig. 45.

Fig. 46., Fig. 47., Fig. 48., Fig. 49.

Fig. 50., Fig. 51., Fig. 52., Fig. 53., Fig. 54.

Fig. 55.

Fig. 56.

Fig. 57.