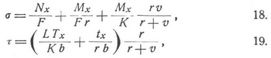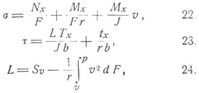Online-Bibliothek

Biegung

[791] Biegung nennt man solche Verschiebungen der Teilchen von Stäben oder Platten, durch welche Formänderungen ihrer Achse oder Achsschicht (s.d. und Achse eines Stabes) bedingt sind. An dieser Stelle soll die elastische Biegung von Stäben zur Sprache kommen (s.a. Feder, Platten). Die Achslinie nach der Biegung heißt elastische Linie (s.d.) oder Biegungslinie. Meist werden nur Fälle behandelt, in welchen die Stabachse ursprünglich, d.h. im spannungslosen Zustande des Stabes bei einer als normal angenommenen [791] Temperatur, gerade oder einfach gekrümmt war, alle äußeren Kräfte in einer Symmetrieebene des Stabes wirken (oder doch in der Ebene durch eine der Hauptträgheitsachsen der Querschnitte, s. Trägheitsmoment) und in jeder Senkrechten zu dieser Biegungsebene der Stabachse überall gleiche Biegungsverhältnisse bestehen oder angenommen werden, so daß es genügt, die Untersuchung der letzteren in der Ebene durchzuführen. Die technische Biegungstheorie geht von gewissen Voraussetzungen aus, durch welche die Gültigkeit ihrer Resultate beschränkt ist (vgl. unten I.). Gewöhnlich sind es die folgenden: a) Die Flächenelemente, welche vor der Biegung auf einem ebenen Querschnitte lagen, bilden auch nach der Biegung eine zur Stabachse senkrechte Ebene. b) Für die Biegung kommen nur die Längenänderungen der zur Achse parallelen Fasern und für diese neben Temperaturänderungen nur die Zug- und Druckkräfte an den Querschnittselementen in Betracht. c) Die Elastizitätsmoduln für Zug und Druck sind innerhalb der Biegungsgrenzen für alle unter b) erwähnten Fasern als gleich und konstant anzusehen (Mittelwerte). Diese Annahmen und Voraussetzungen mögen, soweit nichts Gegenteiliges bemerkt wird, auch im folgenden gelten. Uebrigens pflegt die Annahme betreffend das Ebenbleiben der Querschnitte bei der Formänderung auch dann als Ausgangspunkt zu dienen, wenn die Voraussetzungen b) und c) nicht aufrechterhalten werden (s. z.B. Betoneisenkonstruktionen); sie hat sich bei Versuchen mit Schweißeisen und Flußeisen bis zu sehr weit getriebener Biegung und selbst bei Gußeisen, Granit, Sandstein u.s.w. verhältnismäßig gut bewährt [25], S. 210, 232, 246, [26], S. 34, 436, 438. – Die Hauptaufgabe der technischen Biegungstheorie besteht darin, die mit der Biegung verbundenen Beanspruchungen und Stützenreaktionen zu ermitteln. Daneben interessieren die Formänderungen, mitunter an sich (Einsenkungen u.s.w.), häufiger aber deshalb, weil manche Größen, welche bei Berechnung jener Beanspruchungen bekannt sein müssen, nur aus Beziehungen für die Formänderungen abgeleitet werden können (Stützenmomente durchlaufender und verschiedener einfacher Balken, Horizontalschub von Bogen u.s.w.). Da die Resultate der Biegungstheorie für die wichtigsten Fälle bei der Behandlung der letzteren vorzuführen sind (s.u.a. Balken und Bogen, einfache und durchlaufende, Einsenkung, Elastische Linie, Zug und Druck, exzentrischer, Knickfestigkeit, Nebenspannungen), so wollen wir uns hier auf die Anführung der Grundformeln beschränken.

Für einen beliebigen Querschnitt x mögen bezeichnen M_x das Angriffsmoment (Biegungsmoment), N_x, T_x, V_x, H_x die Normalkraft, Transversalkraft, Vertikalkraft und Horizontalkraft (s. Angriffsmoment, Balken, Bogen), J das Trägheitsmoment (s.d.) in Hinsicht der Achsschicht und ν die positive oder negative Entfernung eines Querschnittelementes von der letzteren. Spannungen heißen im folgenden Beanspruchungen pro Flächeneinheit im Innern der betrachteten Stäbe. Normalspannungen wirken normal, Schubspannungen längs den ergriffenen Flächenelementen (s. Spannung). Alle Formänderungen seien so klein vorausgesetzt, daß die Aenderungen der Stababmessungen gegen deren ursprüngliche Werte vernachlässigt werden dürfen.

I. Biegung horizontaler Balken.

Als horizontale Balken bezeichnet man solche Balken (s.d.), deren Achse stets nur sehr wenig von einer Horizontalen abweicht (so wenig, daß die Tangente des Neigungswinkels gegen 1 vernachlässigt werden kann). Man hat dann bei beliebiger Belastung:

N_X = H_X = 0, T_x = V_x.

1.

Die Normalspannung auf ein Querschnittselement bei υ und die vertikale wie horizontale Schubspannung bei υ (Schubspannung auf ein Querschnittselement und auf ein Flächenelement parallel der Achsschicht daselbst) sind ausgedrückt:

σ = υ/J M_x τ = S_υ/bJ V_x

2.

wobei die υ unterhalb der Achsschicht und die in Fig. 1 angedeuteten Richtungen der M_x, V_x als positiv zu gelten pflegen. b bedeutet die Stabbreite bei ν und Sυ das statische Moment des Querschnittsteils von ν bis zum äußersten Querschnittselement auf der positiven Seite der Achsschicht. Nach der ersten Gleichung 2. erhalten die Fasern auf der einen Seite der Achsschicht Zug, auf der andern Seite Druck; die ersteren werden verlängert, die letzteren verkürzt, die Achsschicht selbst bildet eine neutrale Schicht (s. Achse, neutrale). Für nicht vertikale Flächenelemente bei x, ν können die Normalspannungen und Schubspannungen im allgemeinen, größer werden als σ, τ. Die numerisch größten Werte für irgendwelche Flächenelemente daselbst sind absolut genommen:

[792] worin auch σ ohne Vorzeichen einzusetzen ist (s. Hauptspannungen), doch werden meist nur die Spannungen σ, τ in Betracht gezogen, was in vielen Fällen genügt. Für den ganzen Querschnitt erreicht bτ in der Achsschicht, σ in der größten Entfernung e von der letzteren seinen größten Wert, während speziell für Blechträger (s.d.) das größte N bei Beginn der Gurtung, das größte S zwischen Achsschicht und Beginn der Gurtung, gewöhnlich in einem dieser Grenzpunkte, eintritt. Die größte Normalspannung im Querschnittt x ist nach 2.:

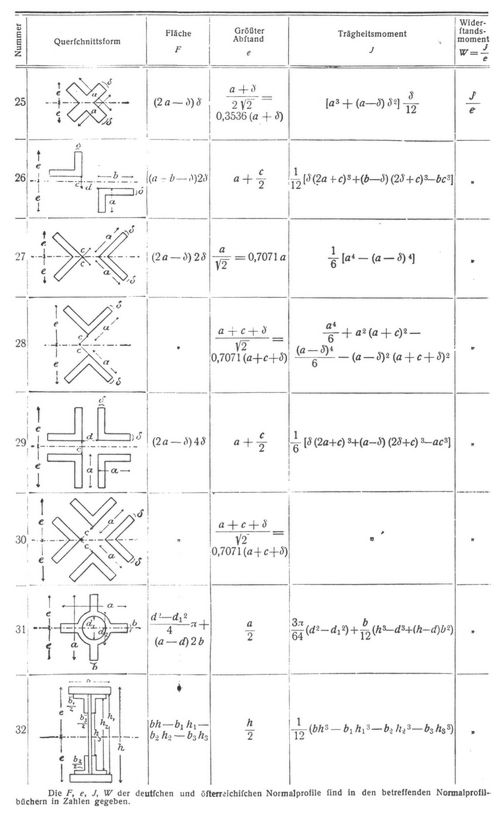
worin das positive oder negative Vorzeichen gilt, je nachdem für das von der Achsschicht entfernteste Querschnittselement υ = e oder υ = – e ist. Der Wert W = J: e heißt das Widerstandsmoment des Querschnitts. In der Tabelle S. 794 ff. sind die e, J, W hinsichtlich der strichpunktiert angedeuteten Achsschicht (bei horizontalen Balken neutrale Achse) für eine Reihe von Querschnitten angeführt. Da bei gleichem Mx der Wert von σ_e zufolge 4. mit wachsendem W abnimmt, so hat man Querschnittsformen von möglichst großem Widerstandsmoment bei bestimmter Fläche eingeführt (I-Träger, Blechträger u.s.w.). Mitunter wird die Form des Stabes so gewählt, daß σ_e für alle Querschnitte den gleichen Wert hat (s. Körper von gleichem Widerstande).

Bezeichnen beim Querschnitt x E den Elastizitätsmodul, ρ den schließlichen Krümmungsradius der Stabachse und σ₁ die Normalspannung der Querschnittselemente bei ν = 1, so hat man:

σ = υ σ₁ = υ/ρ E, M_x = E J/ρ

5.

Denken wir uns in der Biegungsebene ein rechtwinkliges Koordinatensystem mit horizontaler x-Achse und vertikaler y-Achse (Fig. 1) in fester Lage gegen die ursprüngliche Gruppierung der Stabteilchen angenommen und beziehen die Koordinaten y auf die Punkte der schließlichen Stabachse, so folgt aus 5. mit dem durch die Differentialrechnung gelieferten Ausdrucke des Krümmungsradius

die Differentialgleichung der Stabachse oder elastischen Linie:

Die Gleichungen 5., 6. würden unter den Voraussetzungen a) bis c) auch für beliebig große Biegungen gelten [11]. Setzt man jedoch die Biegungen so klein voraus, daß (dy/dx)² gegen 1 vernachlässigt werden kann, so entsteht die Naviersche Biegungsformel:

d²y/dx² = – Mx/E J

7.

welche Navier [1] zuerst mit nachhaltigem Erfolge als Ausgangspunkt der technischen Biegungstheorie gerader Stäbe wählte. Auf Grund von 7. sind z.B. die in den Art. Balken (auch einfache und durchlaufende) gegebenen Ausdrücke der Stützenmomente M, M', Mr und die in der vorletzten Kolumne der Tabelle S. 520, 521 angeführten Einsenkungen f berechnet [6], [15]. S.a. Elastische Linie, Einsenkung.

Daß die Naviersche Gleichung nebst den ihr zugrunde liegenden Voraussetzungen a)–c) (S. 792) auch nach der allgemeinen Theorie der Elastizität für viele praktische Fälle innerhalb der üblichen Beanspruchungen genügen, lassen einschlagende Arbeiten von Saint-Venant, Kirchhoff, Pochhammer [3], [4], [9] erkennen, und manche Versuchsresultate (Ebenbleiben der Querschnitte bei Bauschinger, Considère, Kupffer, Hervortreten der Spannungstrajektorien bei Tetmajer u.s.w.), zahlreiche Beobachtungen an ausgeführten Konstruktionen (Einsenkungen, Formänderungen durchlaufender Balken u.s.w.) und jahrzehntelange Erfahrungen mit den auf Grund jener Annahmen berechneten eisernen Trägern scheinen für ihre vielfache Zulässigkeit zu sprechen. Anderseits beruhen auch die in Frage kommenden Teile der allgemeinen Elastizitätslehre auf Voraussetzungen, welche für technisch wichtige Materialien nicht einmal annähernd zutreffen (Isotropie des Materials, gleiche und konstante Elastizitätsmoduln für Zug und Druck u.s.w.), die praktischen Fälle entsprechen nicht immer genügend den Voraussetzungen der erwähnten theoretischen Ableitungen (die Querschnittsdimensionen verschwinden nicht gegen die Länge u.s.w.), und die gebräuchlichen Annahmen umfassen nicht alle Einwirkungen, deren Berücksichtigung unter Umständen geboten sein kann (Temperaturänderungen, Reibungen an den Auflagern u.s.w.), wie dieselben auch keinesfalls bis zum Bruche gelten. So haben lieh mehrfach Abweichungen von den gewöhnlichen Formeln als notwendig erwiesen.

Die Gleichheit und Unveränderlichkeit der Elastizitätsmoduln für Zug und Druck gilt zwar innerhalb gewisser Grenzen annähernd für Schweißeisen, Flußeisen und Stahl, nicht aber z.B. für Gußeisen. Dementsprechend fand Considère, daß die neutrale Schicht bei diesem fast von Beginn der Biegung an von der Achsschicht abwich und z.B. bei einem bearbeiteten (von der Gußhaut befreiten) quadratischen Stabe von 2,01 cm Stärke und 1 m Spannweite bis 0,614 der Höhe von den äußersten Zugfasern gegen die Druckseite gelangte. Die auf Grund von 4. ermittelte Biegungsfestigkeit (größte rechnungsmäßige Normalspannung im Bruchquerschnitt) war b = 2063 kg/qcm oder β = 1,83 mal so groß als die für dasselbe Gußeisen bei gewöhnlichen Zugversuchen erhaltene Fertigkeit z = 1130 kg. Bei Versuchen mit runden Gußeisenstäben von[796] 2,03 cm Durchmesser erhielt Considère β = 2,17 und 2,25, während die französische Bauverwaltung früher allgemein β = 2 annahm. Nach Considère [14], S. 96 u. f., und Bach [25], S. 237 u. f., überschreriet b den Wert von ζ um so mehr, je mehr sich das Material nach der Achsschicht hin zusammendrängt; für einen quadratischen Stab mit horizontaler Diagonalschicht beispielsweise erhielt Bach ß = 2,35 (s.a. Biegungsfestigkeit). Daneben machte sich bei Versuchen Bachs mit unbearbeiteten Stäben ein Einfluß der Gußhaut auf Verminderung von β (um etwa ¹/₆) bemerkbar.

Wie Gußeisen, so weicht auch das als Konstruktionsmaterial für Hallenbedachungen viel verwendete Glas stark von der gewöhnlichen Biegungstheorie ab, was sich auch bei ihm schon darin zeigt, daß die neutrale Schicht nicht mit der Achsschicht zusammenfällt [17], S. 13. Bei Versuchen von Connert ergab sich, daß die Glasdicke von wesentlichem Einfluß auf jene Abweichungen ist, während letztere für Weichglas und Hartglas so verschieden ausfielen, daß sie nur durch besondere Formeln für beide Fälle dargestellt werden konnten [17], S. 109. Soweit die gewöhnlichen Biegungsformeln bei Holz, Stein, Beton u.s.w. zur Verwendung kommen, sind sie natürlich ebenfalls nur als Notbehelfe aufzufallen, da die Elastizitätsmoduln dieser Körper für Zug und Druck nicht gleich und stark veränderlich sind (vgl. Elastizitätsmodul, Elastizitätsgesetz, Zugelastizität, Druckelastizität). Indessen erhält man bei Berücksichtigung dieser Verhältnisse Biegungsformeln, welche für praktische Zwecke im allgemeinen zu umständlich sind [22], [23], [24].

Während die Abweichungen der neutralen Schicht von der Achsschicht bei Gußeisen, Stein u.s.w. schon durch die Verschiedenheit der Elastizitätsmoduln für Zug und Druck erklärlich erscheinen, fand Flamant auf Grund der allgemeinen Elastizitätslehre, daß die neutrale Schicht auch abgesehen hiervon und von der mangelnden Isotropie des Materials bei oben angreifender Last etwas nach oben, bei unten angreifender etwas nach unten rückt [20], S. 239, 242, was vorausgegangene Versuche von Wilson mit ausgeglühten rechteckigen Glasstäben bestätigten [20], S. 246. Doch nahmen die Abweichungen mit wachsendem l : h rasch ab (l Spannweite, s. Biegungselastizität Fig. 1, h Querschnittshöhe), so daß sie schon für l: h = 6 nur noch etwa h: 25 betrugen [20], S. 240.

Der Einfluß der vertikalen Schubspannungen τ auf die Biegung wurde zuerst, wenn auch nicht allgemein genügend (die Veränderlichkeit von τ mit der Entfernung von der Achsschicht blieb unberücksichtigt), von Poncelet [2] (deutsche Ausgabe S. 193, vgl. [8], S. 213), dann aber schärfer und ausführlich von Castigliano [13] (S. 141, deutsche Ausgabe S. 135) verfolgt, wie auch besonders von Winkler in Betracht gezogen [16], S. 90. Bach und Mantel fanden, daß dieser Einfluß bei Bestimmung des Elastizitätsmoduls aus Biegungsversuchen zu berücksichtigen ist (s. Elastizitätsmodul), da die bekannte Tatsache, daß solche Versuche E auf Grund der sonst eintretenden Formel für die Einsenkung (s. Biegungselastizität) oft wesentlich kleiner als Zugversuche ergeben, aus ihm vollständig erklärt werden konnte. Es liegt hierin eine neue Bestätigung der Biegungstheorie im allgemeinen. Die Naviersche Biegungsformel mit Berücksichtigung des Einflusses der vertikalen τ lautet:

oder auch:

Mittels dieser Formel sind z.B. die in der Tabelle S. 520, 521 gegebenen Einsenkungen mit Rücksicht auf die τ oder auf V_x berechnet. S.a. Biegungselastizität, Einsenkung, Elastische Linie.

In 8., 9. bedeutet G den Schubelastizitätsmodul (s.d.) und k einen vom Querschnitt allein abhängigen Koeffizienten, der allgemein durch

ausgedrückt ist, bei Erstreckung des Integrals auf alle Querschnittselemente dF. Man erhält z.B. für Quadrat und Rechteck k = ⁶/₅, für den Kreis und gewöhnlich genügend genau auch für die Ellipse k = ^l0/₉, für den rechteckigen, Ring, I-Querschnitt und [-Querschnitt mit den in Tabelle S. 794, Nr. 6–8, verwendeten Bezeichnungen und b₁ = mb, h₁ = nh:

Diese Gleichung liefert für m = 0 oder n = 0 oder n = l wieder den dem Rechteck entsprechenden Wert ⁶/₅, und weiter

Die in kleiner Schrift beigesetzten Werte ergeben sich aus der von Winkler [16], S. 108, für symmetrische Blechträgerquerschnitte ermittelten Näherungsformel

K = F/hd

12.

[797] die auf der Voraussetzung beruht, daß sich die Vertikalkraft V_x allein und gleichmäßig auf die Vertikalplatte von der Dicke d und der ganzen Trägerhöhe h verteilt. (Für Blechträger sind die Schubspannungen τ von der bis zum Beginn der Gurtungen wenig veränderlich und für die Gurtungen klein, also von geringem Einfluß, vgl. Blechträger). Die Formel ist auch für die üblichen I-Träger, denen mit den in 11. verwendeten Bezeichnungen die Form

k = 1 – mn/1 – m

13.

entspricht, genügend genau. Für die deutschen Normalprofile

Nr. 10

14

17

24

30

40

50

ergab Gleichung 11.:

k = 2,43

2,36

2,30

2,27

2,20

2,11

2,06,

dagegen Gleichung 13.:

k = 2,37

2,31

2,25

2,22

2,15

2,05

2,01,

und 12. mit dem im deutschen Normalprofilbuch angeführten F:

k = 2,37

2,30

2,26

2,22

2,14

2,05

2,00,

während Mantel [19], S. 100, graphisch mit Berücksichtigung der Flanschenneigungen und Abrundungen erhielt:

k = 2,34

2,28

2,25

2,18

2,13

2,08

2,03.

Ueber graphische Ermittlung von k für andre Querschnitte s. [18], S. 148, 168.

Bei Drehbrücken, die als durchlaufende Balken mit zwei Oeffnungen angeordnet waren, hat man mitunter bei starker Sommerhitze die Trägerenden derart fest aufsitzend gefunden, daß eine Drehung erst vorgenommen werden konnte, nachdem der Obergurt einige Zeit mit einer Holzhülle bedeckt war (schlechter Wärmeleiter, vgl. [7]). Dies zeigt einen Einfluß der Wärme auf solche Träger, der verfolgt werden mußte, wenn die ungünstigsten Beanspruchungen und die nötigen Kräfte zur Drehung für alle Fälle angegeben werden füllten. Ist auf irgendwelche Art, z.B. weil der Untergurt bei obenliegender Fahrbahn vor direkter Einwirkung der Sonne geschützt war, beim Querschnitt x eine Differenz t = t_o – t_u der Temperaturen von Oberkante und Unterkante des Trägers entstanden, und denkt man sich diese Differenz auf die Trägerhöhe gleichmäßig verteilt, so folgt der mit Rücksicht auf diesen Einfluß verallgemeinerte Ausdruck der Navierschen Formel [10]

während 7. nur gleichmäßige Temperaturänderungen für einen ganzen Querschnitt zuläßt. In 14. bedeutet α den linearen Ausdehnungskoeffizienten (s.d.) des Trägermaterials, t wie die übrigen Größen können mit x veränderlich sein. Mit Hilfe von 14. unter Voraussetzung eines konstanten t sind die in dem Art. Balken, durchlaufende, unter »Temperatureinflüsse« angeführten Formeln erhalten [15], S. 150. Aehnliche Einflüsse können auch für einfache Balken mit Stützenmomenten auftreten; vgl. Elastische Linie.

II. Einfach gekrümmte Stäbe.

Es seien beim Querschnitte x vor der Biegung r der Krümmungsradius der Stabachse, υ die positive oder negative Entfernung eines Querschnittselements dF von der Achsschicht, und wenn p die Entfernung der äußersten Faser auf der positiven, dem Krümmungsmittelpunkt entgegensetzten Seite der Achsschicht von der letzteren bedeutet:

Das Integral in 15. ist auf alle Querschnittselemente zu erstrecken. Die Produkte αt aus Ausdehnungskoeffizient α und die Temperaturänderung t (Zunahme positiv) gegen die angenommene Normaltemperatur werden bei allen Querschnittselementen gleich groß vorausgesetzt, während

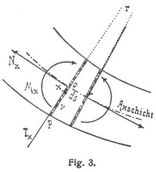
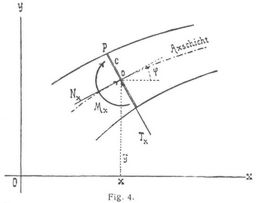
entweder drückende σ und die in Fig. 2 angedeuteten Richtungen von Mx, Nx, T_x als positiv gelten können (wobei Mx die anfängliche Krümmung zu vermindern sucht, N_x Druck bedeutet und T_x vom Krümmungszentrum weggerichtet ist), oder ziehende σ und die in Fig. 3 angedeuteten Richtungen von M_x, Nx, T_x. Ersteres ist bei elastischen Bogenträgern üblich. In beiden Fällen sind die Normalspannung σ und die Querschubspannung und Längsschubspannung τ (Schubspannung auf Flächenelemente senkrecht und parallel der Achsschicht) bei υ ausgedrückt [21], § 3:

unter b die Trägerbreite bei x, υ, unter tx denjenigen Teil von T_x verbanden, der auf den Querschnittsteil von υ bis p kommt.[798] Derselbe könnte, wenn man 19. ohne Vernachlässigung verwenden wollte, zunächst aus der einfacheren Gleichung 25. berechnet werden, doch sind die Schubspannungen τ bei den hier in Frage kommenden Aufgaben (insbesondere betreffend elastische Bogenträger) im allgemeinen nur annähernd berechnet oder überhaupt nicht in Betracht gezogen worden. Auch die schiefen Spannungen, deren größte Absolutwerte wieder durch 3. bestimmt sind, wurden mein unberücksichtigt gelassen.

Während das durch 17. ausgedrückte statische Moment Sυ des Trägerteils von υ bis p in Hinsicht der Achsschicht und das Trägheitsmoment

des ganzen Querschnitts in Hinsicht derselben nur vom Querschnitt x selbst abhängen, ist das Krümmungsmoment K nach 15. auch vom Krümmungsradius r der Stabachse bei x abhängig. Setzt man allgemein:

K = φ J,

21.

so findet sich z.B. für quadratische und rechteckige Querschnitte von der Höhe h = 2e:

für kreisförmige und elliptische Querschnitte von Höhe h = 2e:

während sich beispielsweise für folgende Querschnitte und r : h die beigesetzten φ ergeben [21], § 5:

Hiernach kann in den meinen Fällen J an Stelle von K gesetzt werden. Damit vernachlässigt. man zufolge 15., 20. die Entfernungen ν der Querschnittselemente gegen den Krümmungsradius r. Geschieht dies auch in 18., 19., 16., so folgen:

und wenn, wie bei elastischen Bogenträgern üblich, noch die Glieder mit r im Nenner gegen die übrigen vernachlässigt werden:

Nach 18., 22., 25. erreicht α für einen Querschnitt x seine äußersten Werte in den beiderseits am weiteren von der Achsschicht gelegenen Querschnittselementen (vgl. a. Blechträger, Kernlinien), während bτ mit Rücksicht auf die Ausdrücke von L in diesen Elementen 0 wird und z.B. auf Grund von 25. wie bei horizontalen Balken (s. oben I.) in der Achsschicht seinen größten Wert annimmt.

Wir wollen, besonders im Hinblick auf elastische Bogenträger, noch einige weitere Formeln beifügen, wobei drückende σ als positiv gelten und die positiven Richtungen von M_x, N_x, T_x entsprechend Fig. 2 gewählt werden. Ein rechtwinkliges Koordinatensystem von fester Lage gegen die anfängliche Gruppierung der Stabpunkte sei in der Biegungsebene so angenommen, daß die x-Achse auf der gleichen Seite der Achsschicht wie das anfängliche Krümmungszentrum bei x liegt, und die positive Richtung der y von der Seite des letzteren nach der entgegengesetzten geht. Als Koordinaten x, y eines Querschnittes x gelten die anfänglichen Koordinaten seines in der Stabachse liegenden Schwerpunktes, während s die anfängliche Achslänge von 0 bis x und φ den anfänglichen Winkel der Stabachse bei x mit der positiven Richtung der x-Achse bedeuten. Bezeichnen dann Δx, Δy, Δs, Δφ die Aenderungen von x, y, s, φ, die diesen Größen gegenüber verschwindend klein vorausgesetzt werden, dann hat man:

worin:

[799] oder, wenn, wie für 22.–24., alle υ gegen r vernachlässigt werden, neben 29.:

und wenn noch, wie für 25., die Glieder mit r im Nenner gegen die übrigen vernachlässigt werden,

Auf Grund von 26.–28. mit Υ, Z nach 29., 31. sind z.B. die unter Bogen, einfache und durchlaufende, gegebenen Ausdrücke des Horizontalschubes H und der Endmomente, MM' berechnet [21]; s.a. [15], A. 54, 55.

III. Gerade Stäbe von beliebiger Richtung.

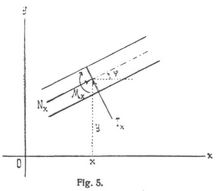
Für solche gelten K = J, L = S_υ und die Gleichungen 25., 32. unter den Voraussetzungen a)–c) (S. 792) genau, da ihnen in 15., 16., 22., 23., 29., 30. r = ∞ entspricht (Fig. 5). Werden die x-Achse parallel oder doch so nahe einer Parallelen zur Stabachse gelegt, daß ds = dx gesetzt werden darf und die Ordinaten y im vorliegenden Falle auf die schließliche Stabachse bezogen (vor der Formänderung wären sie für eine Abszissenachse parallel der Stabachse alle gleich), dann hat man für die zuletzt betrachteten kleinen Formänderungen:

und damit nach 32. die Naviersche Biegungsgleichung

die demnach auch bei Auftreten von Axialkräften Nx und Temperaturänderungen gilt, vorausgesetzt, daß letztere für je einen ganzen Querschnitt gleich groß sind (vgl. Formel 14.). Sollen die Momente, wie für 7., als positiv gelten, wenn sie die Krümmung nach der x-Achse (mit Krümmungszentrum von der Achsschicht aus in der Richtung nach der x-Achse) zu vergrößern streben (Fig. 1, 6), dann hat man in 25., 32., 33. – Mx an Stelle von M_x zu setzen. Werden ziehende Nx, σ als positiv angesehen, so treten in 25., 32. – Nx, – σ an die Stellen von Nx, σ. – Anwendungen der Formeln für gerade Stäbe von beliebiger Richtung kommen bei Betrachtung der Knickfestigkeit, exzentrischen Druckbeanspruchung und Zugbeanspruchung, Nebenspannungen von Fachwerken u.s.w. vor; s.a. [15], A. 54, 55, 56, 58, 107.

Literatur: [1] Navier, Résumé des leçons données à l'école royale des ponts et chaussées sur l'application de la mécanique à l'établissement des constructions et des machines, Paris 1826 (3. Auflage mit Ergänzungen von Saint-Venant, Paris 1864; deutsche Ausgabe Hannover 1879). – [2] Poncelet, Cours de mécanique appliquée aux machines, Metz 1826 (2. Aufl. Metz 1837; deutsche Ausgabe Darmstadt 1848). – [3] de Saint-Venant, Mémoire sur la flexion des prismes, Liouvilles Journal, I, 1856; Clebsch, Theorie der Elastizität fester Körper, Leipzig 1862, S. 70. – [4] Kirchhoff, Ueber das Gleichgewicht und die Bewegung eines unendlich dünnen elastischen Stabes, Crelles Journal 1859, LVI, S. 285. – [5] Winkler, Die Lehre von der Elastizität und Festigkeit, Prag 1867. – [6] Weyrauch, Allgemeine Theorie und Berechnung der kontinuierlichen und einfachen Träger, Leipzig 1873. – [7] Steiner, Ueber den Einfluß einer ungleichmäßigen Erwärmung der Gurte auf kontinuierliche Träger, Wochenschr. d. österr. Ing.- u. Arch.-Vereins 1877, S. 292. – [8] Grashof, Theorie der Elastizität und Festigkeit, Berlin 1878. – [9] Pochhammer, Untersuchungen über das Gleichgewicht des elastischen Stabes, Kiel 1879. – [10] Weyrauch, Temperatureinflüsse bei kontinuierlichen Trägern, Zeitschr. f. Baukunde 1879, S. 437. – [11] Saalschütz, Der belastete Stab unter Einwirkung einer seitlichen Kraft, Leipzig 1880. – [12] Müller-Breslau, Theorie und Berechnung eiserner Bogenbrücken, Berlin 1880. – [13] Castigliano, Théorie de l'équilibre des systèmes élastiques, Turin 1880 (deutsche Ausgabe, Wien 1886). – [14] Considère, Mémoire sur l'emploi du fer et de l'arcier, Paris 1885 (auch Annales des ponts et chaussées, 1885, I). – [15] Weyrauch, Aufgaben zur Theorie elastischer Körper, Leipzig 1885. – [16] Winkler, Theorie der Brücken, 1. Heft: Aeußere Kräfte der Balkenträger, Wien 1886. – [17] Connert, Ueber die Biegungsfestigkeit des Glases, Civilingenieur 1888, S. 1, 109, 621. – [18] Ritter, Anwendungen der graphischen Statik, I.: Die im Innern eines Balkens wirkenden Kräfte, Zürich 1888. – [19] Mantel, Zum Einfluß der Schubspannungen u.s.w., Schweiz. Bauzeitung 1889, I, S. 99. – [20] Flamant, De l'influence sur la flexion des poutres de la position superficielle des charges, Annales des ponts et chaussées 1893, II, p. 228. – [21] Weyrauch, Elastische Bogenträger, ihre Theorie und Berechnung entsprechend den Bedürfnissen der Praxis, München 1896. – [22] Latowski, Die Biegungselastizität bei Körpern von ungleicher Festigkeit, Zeitschr. d. Vereins deutsch. Ing. 1897, S. 941. – [23] Engesser, Widerstandsmomente und Kernfiguren bei beliebigem Formänderungsgesetz, Zeitschr. d. Ver. deutsch. Ingenieure 1898, S. 903, 927. – [24] Schule, Die Biegungslehre gerader Stäbe mit veränderlichem Dehnungskoeffizienten, Dinglers Polyt. Journal 1902, S. 149. – [25] Bach, Elastizität und Fertigkeit, Berlin 1902. – [26] v. Tetmajer, Die angewandte Elastizitäts- und Festigkeitslehre, Leipzig und Wien 1904. – S.a. die Literatur unter Balken, Bogen (einfache und durchlaufende), Biegungsfestigkeit, Blechträger, Einsenkung, Elastizitätsmodul u.s.w.

Weyrauch.