Online-Bibliothek

Zugversuch

[1030] Zugversuch, die am meisten verbreitete statische Probe zur Bestimmung der Fertigkeit und Zähigkeit der Baustoffe. Man läßt (abgesehen von der Prüfung ganzer Konstruktionsteile) auf einen geraden stabförmigen Körper äußere Kräfte derart wirken, daß sie parallel zur Achse des Stabes gerichtet sind, den Stab zu verlängern streben und sich möglichst gleichmäßig über den Stabquerschnitt verteilen.[1030]

Beobachtet werden beim vollständigen Zugversuch: die Belastungen an der Proportionalitäts-, Elastizitäts- und Streckgrenze, die höchste vorn Stabe getragene Belastung, die Bruchlast, und die Belastung im Augenblick des Bruches, die Zerreißlast, ferner die Dehnung mit fortschreitender Belastung und nach dem Bruch sowie die Verminderung des Querschnittes (Kontraktion) an der Bruchstelle. Die Probestäbe für den Zugversuch unterscheidet man, abgesehen von Sonderuntersuchungen an Drähten, Seilen und Riemen, bei denen die Prüfung an nicht weiter zugerichteten Abschnitten vorgenommen wird, nach der Form des Querschnittes in Rundstäbe mit kreisrundem und in Flachstäbe mit quadratischem oder rechteckigem Querschnitt.

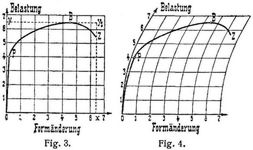
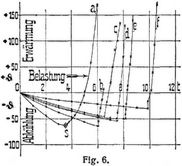
Die normale Form des Rundstabes (vom Internationalen Verbände für die Materialprüfung der Technik als solche angenommen) zeigt Fig. 1. Flachstäbe werden in der Regel nach Fig. 2 hergerichtet. Von den verstärkten Enden, den sogenannten Köpfen, welche zur Einspannung in die Zerreißmaschine dienen (s. Einspannvorrichtungen) überführen bei den Normalrundstäben konische Strecken und bei den Flachstäben Hohlkehlen mit hinreichend großem Halbmesser zu dem mittleren zylindrischen oder prismatischen Stabteil. Seine Gesamtlänge (l g) heißt Versuchs- oder Gebrauchslänge. Auf ihr wird vor dem Versuch durch zwei Körner- oder Strichmarken eine bestimmte Länge, die Meßlänge l, zur Ermittlung der Dehnung nach dem Bruch abgegrenzt. Häufig wird die Meßlänge zur Ausübung eines später zu besprechenden Meßverfahrens mit Unterteilung versehen [28], [29], [53]. Die Abstände (l_t) ihrer einzelnen Marken nennt man Teilungsintervall oder Teilungslänge. Die Beziehungen zwischen den jeweiligen Belastungen (Kräften) und zugehörigen Formänderungen des Probestückes werden durch Schaulinien dargestellt. Sie werden entweder durch punktweises Auftragen der von der Festigkeitsprobiermaschine angezeigten Belastung als Ordinate und der zugehörigen, mit besonderen Meßapparaten festgestellten Formänderung, der Dehnung beim Zugversuch, als Abszissen erhalten oder von der Festigkeitsprobiermaschine mit Schreibapparat selbsttätig aufgezeichnet. Das zugehörige Koordinatensystem ist in der Regel das geradlinigrechtwinklige, orthogonale, Fig. 3. Bei den selbsttätigen Schaulinienzeichnern findet sich indessen nicht seiten die eine der beiden Koordinaten, und zwar besonders diejenige für die Belastung, als Kreisbogen verlaufend (Fig. 4).

Um die Eigenschaften verschiedener Materialien an Hand der Schaulinien in Vergleich stellen zu können, sind entweder alle Versuche mit Probestäben von genau den gleichen Abmessungen auszuführen oder die Schaulinien sind nicht nach Belastungen und Gesamtformänderungen, sondern nach Spannungen, Belastungen bezogen auf die Querschnittseinheit, und nach den Formänderungen, bezogen auf die Längeneinheit, aufzutragen. Dann ist dasjenige Material, bei dem die Schaulinie die größte Höhe erreicht, die größten Ordinate aufweist, das festeste und dasjenige mit der Schaulinie größter Länge in der Richtung der Abszisse das formänderungsfähigste.

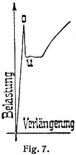
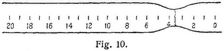
Den verschiedenartigen Verlauf der Verlängerung bei stetig fortschreitender Belastung zeigen die Schaulinien a–c, Fig. 5. Die Linien a und b steigen bis P geradlinig an, d.h. die Verlängerung ist der Belastung proportional. Man nennt daher die durch die Ordinate von P gemessene Kraft die Belastung an der Proportionalitätsgrenze oder kurz Proportionalitätsgrenze. Ihr entspricht die Verlängerung λ_p. Sie ist für die Längeneinheit des Stabes nur gering, und daher kann die Proportionalitätsgrenze an den gebräuchlichen kurzen Probestäben nur mit Hilfe von Feinmeßapparaten (Spiegelapparaten, Mikrometer u.s.w., s. Dehnungsmesser) ermittelt werden, indem die Belastung stufenweise gesteigert und die Verlängerung jedesmal abgelesen wird. – Die Belastung, nach der beim Entlasten zuerst bleibende Verlängerung, ein Dehnungsrest, sich ergibt, heißt Elastizitätsgrenze. Sie fällt meist mit der Proportionalitätsgrenze zusammen, zuweilen liegt sie tiefer. Ihre Bestimmung ist abhängig von der Feinheit des Meßverfahrens und von der Dauer der Entlastung, indem der sofort nach dem Entlasten beobachtete Dehnungsrest infolge der elastischen Nachwirkung [1] bei längerer Entlastung sich allmählich verringert. Um zu einer einheitlichen Bestimmung der [1031] Elastizitätsgrenze zu gelangen, ist vorgeschlagen, diese Grenze bei derjenigen Belastung anzunehmen, die eine bestimmte bleibende Dehnung hinterläßt, z.B. 0,03% der ursprünglichen Länge. – Oberhalb von P sind beide Schaulinien a und b (Fig. 5) gekrümmt, die konkave Seite der Abszissenachse zugewendet, d.h. die Dehnungen wachsen nach Ueberschreitung der Proportionalitätsgrenze in stärkerem Maße als die Belastungen. Bei Materialien mit den durch die Schaulinie a dargestellten Eigenschaften verlängert sich der Stab unter der dem Punkt S entsprechenden Belastung zunächst beträchtlich, bevor er höhere Belastungen zu tragen vermag. Man sagt, der Stab »streckt« oder er »fließt« [2]–[4] und nennt diese Belastung die Streck- oder Fließgrenze mit der zugehörigen Verlängerung λ_s. Beim Versuch ist eine derartig scharf ausgeprägte Streckgrenze leicht an folgenden Erscheinungen zu erkennen: 1. Bei gleichbleibender Arbeitsgeschwindigkeit des Spannwerkes der Festigkeitsprobiermaschine erfordert die Steigerung der Belastung um die die Streckgrenze umfassende Laststufe erheblich mehr Zeit als die vorhergehenden Laststufen. Häufig fällt der Wagenhebel sogar unter der Belastung plötzlich ab. 2. Bei Stäben mit Walzhaut (Zunder) springt letztere ab, da sie weniger dehnbar ist als das darunterliegende Material. 3. Sauber bearbeitete Staboberflächen werden rauh und zeigen Fließfiguren [5]–[8], [53], und 4. tritt die erste mit rohen Meßwerkzeugen wahrnehmbare Verlängerung ein. – Beim Verlauf des Versuches nach Schaulinie b (Fig. 5) ist die Streckgrenze nicht scharf ausgeprägt. Ihre Festsetzung bleibt daher mehr oder weniger willkürlich [9]. Materialien mit Schaulinien nach c (Fig. 5) haben weder Proportionalitäts- noch Streckgrenze. Um trotz des geschilderten verschiedenartigen Verhaltens der Materialien die Streckgrenze einheitlich festzulegen, ist es neuerdings eingeführt, diejenige Belastung als Streckgrenze anzusehen, bei der die bleibende Dehnung des Stabes 0,2% seiner ursprünglichen Länge noch nicht erreicht. – E. Rasch [50] hat vorgeschlagen, die Streckgrenze nach der Temperaturänderung bei steigender Belastung elektrisch mit Galvanometer und Thermoelement zu bestimmen. Die Lötstelle des Thermoelements (Eisen-Konstantan) wird mit einer Spange gegen die Staboberfläche gepreßt. Ein an das Thermoelement angeschlossenes Galvanometer (Spiegelgalvanometer mit Lichtzeiger) zeigt die Temperaturänderungen des Probestabes während des Zugversuches an. Wird ein Zugstab elastisch gedehnt, so kühlt er sich ab (vgl. Expansion der Gase). Wird jedoch die Zugkraft P stetig gesteigert, so treten zu den elastischen Dehnungen nach und nach bleibende Formänderungen. Dieser auf innere Reibung entfallende Teil der Dehnungsarbeit wird in Wärme umgewandelt. Der thermodynamische Gleichgewichtszustand wird dann überschritten, wenn die Wärmeerzeugung gleich oder größer wird als die Abkühlung durch elastische Dehnungsarbeit. Dieser kritische Punkt S gibt sich durch eine ausgeprägte Umkehr der Galvanometeranzeige θ zu erkennen (vgl. die Diagramme Fig. 6 aus wiederholten Versuchen a–f mit demselben Probestabe aus Messing). Bei sehr scharf ausgeprägter Streckgrenze nimmt die Schaulinie häufig auch den Verlauf nach Fig. 7. Man spricht dann von einer »oberen« und einer »unteren« Streckgrenze, entsprechend den Ordinaten der Punkte o und u [3], [51]. Die »obere« Streckgrenze ist diejenige Spannung, bei der das Strecken beginnt, die »untere« die kleinste Spannung, bei der es noch vor sich geht. Beide liegen oft weit auseinander. So fand Bach [51] Unterschiede bis zu 50% (19,9 : 29,7 kg/qmm). Sie ergeben sich bei dem geglühten Material größer als bei dem ungeglühten. Ferner fand Bach, daß besonders die »obere« Streckgrenze stark abhängig ist von der Querschnittsform des Stabes [52]; sie lag bei kreisrundem Querschnitt höher als bei quadratischem oder gar 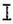-förmigem.

Aus dem Bildungsgang der Fließfiguren und dem Verlauf im Abspringen der härteren Walzhaut erkennt man, daß das Fließen an einer Stelle beginnt, sich dann in der Regel über die ganze Versuchslänge fortpflanzt und daß hierauf alle Querschnitte zunächst gleichmäßig an der Verlängerung des Stabes teilnehmen [5] (s.a. Fließfiguren). Die Belastung steigt nach Ueberschreitung der Streckgrenze noch mehr oder weniger an, bis sie bei B Fig. 3–5 ihren höchsten Wert erreicht, den man mit Bruchlast (B) bezeichnet. Unter dieser Last verlängert sich der Stab besonders innerhalb einer geringen Strecke; sein Querschnitt verjüngt sich örtlich, der Stab »schnürt ein«. Mit dieser starken Abnahme des Querschnitts verringert sich zugleich die Tragfähigkeit des Stabes, bis er unter der durch die Ordinate von Z gemessenen Belastung, der Zerreißlast (Z), zu Bruch geht. Der Bruch beginnt hierbei in der Regel im Kern des Stabes [10]–[13]. Stäbe mit der Schaulinie c (Fig. 5) zeigen meist keine örtliche Einschnürung: sie zerreißen unter der Höchstlast B. – Die von der Schaulinie gegen die Abszissenachse abgegrenzte Fläche stellt die Zerreißungsarbeit (A) dar. Das Größenverhältnis dieser Fläche zu der Fläche a des umschriebenen Rechtecks o y y₁ x (Fig. 3) heißt Völligkeitsgrad (ξ). Um die an Stäben von verschiedenen Abmessungen ermittelten Ergebnisse in Vergleich stellen zu können, hat man die Belastungen auf die Einheit des Stabquerschnittes und die Verlängerungen l auf die Einheit der Meßlänge (/) umzurechnen, d.h. anstelle der Belastungen die Spannungen (σ) und statt der Verlängerungen die Dehnungen (ε = λ/l) in Betracht zu ziehen. Der Berechnung der Spannungen, σ_P = P : F an der Proportionalitätsgrenze, σ_S = S : F an der Streckgrenze und σ_B = B : F der Bruchspannung, wird der ursprüngliche Stabquerschnitt (F) zugrunde gelegt, der Berechnung der Zerreißspannung σ_Z = Z : f dagegen der Querschnitt (f) an der Bruchstelle. – Ist die Schaulinie nach Spannungen und Dehnungen verzeichnet, so liefert die von ihr[1032] abgegrenzte Fläche die spezifische Zerreißungsarbeit (a = A : J) für die Einheit (cmm oder ccm) der Stabmaße (J) innerhalb der Meßlänge. Der Völligkeitsgrad (ξ) ist für Materialien gleicher Gattung konstant [14]; daher kann man an Stelle der Flächen a auch die Fläche des umschriebenen Rechtecks (a : ξ = σ_B · ε_Z = Bruchspannung mal Bruchdehnung) unmittelbar vergleichen. Bei technischen Untersuchungen wird die Dehnung in der Regel nicht auf die Längeneinheit bezogen, sondern in Hundertteilen der Meßlänge angegeben. Die prozentuelle Dehnung δ ist dann: δ = 100λ : l. Ebenso wird auch die Querschnittsverminderung (q) an der Bruchstelle in Hundertteilen des ursprünglichen Querschnitts berechnet nach der Gleichung q = 100 (F – f) : F.

Wertziffern oder Qualitätszahlen sind Zahlenwerte, welche den Gebrauchswert oder die Widerstandsfähigkeit des Materials gegen die Inanspruchnahme ihrer Festigkeit im Betriebe, bedingt durch Fertigkeit und Zähigkeit, zum Ausdruck bringen sollen. Die älteste Wertziffer ist die Wöhlersche [15]. Sie ist gegeben in der Summe aus Bruchspannung und Querschnittsverminderung (σ_B + q); sie soll aber um ein Bestimmtes größer sein als die Summe der für beide Größen vorgeschriebenen Einzelwerte, damit ein Weniger an Fertigkeit durch größere Zähigkeit und umgekehrt ersetzt werden kann. Tetmajer führte die Zerreißungsarbeit oder das Arbeitsvermögen (σ_B · δ) als Wertziffer ein [14]. Urteile über die Bedeutung beider Wertziffern finden sich [16]–[23].

Umstände, welche das Ergebnis des Zerreißversuches beeinträchtigen, sind:

1. Die Art der Entnahme und Zurichtung der Proben. Die Entnahme hat auf kaltem Wege mit Hilfe schneidender Werkzeuge, am betten mittels Kaltsäge oder auf der Hobelmaschine zu erfolgen. Mit der Schere abgeschnittene Blechstreifen sind unter der Presse oder mittels weicher Hämmer kalt gerade zu richten und längs der Schnittkanten abzuarbeiten, um den Einfluß des Scherenschnittes [24] zu beseitigen. Zerreißproben aus größeren Schmiedestücken [25] und Gußstücken liefern, an der Oberfläche entnommen, meist höhere Fertigkeit als die in der Mitte gelegenen. Bei Zerreißversuchen mit Schienenmaterial werden in der Regel Flachstäbe aus Fuß und Steg und Rundstäbe aus Mitte Schienenkopf entnommen. Tetmajer empfiehlt [26], auch aus dem Kopf Flachstäbe, und zwar unmittelbar unter der Lauffläche zu entnehmen, um etwa hier vorhandene Ungänzen aufzudecken, von denen die Dauerhaftigkeit der Schienen abhängt und die dadurch entstehen können, daß die Blasen bei Rückkohlung mittels siliciumreicher Zuschläge oder infolge zu heißen Gusses [27] an die Oberfläche des Blockes getrieben wurden. – Flachstäbe von der Dicke des Walzstückes (z.B. aus Blechen, Flacheisen u.s.w.) bleiben auf den Breitseiten unbearbeitet, um die Walzhaut zu erhalten [28] und [29]. Im übrigen müssen bearbeitete Flächen der Länge nach abgezogen werden, da Querrisse in der. Oberfläche das Ergebnis beeinträchtigen, besonders bei hartem Stahl und Kupfer. – Bei Walzstücken ist zwischen Längs- und Querproben zu unterscheiden. Die ersteren haben beim Schweißeisen erheblich größere Fertigkeit und Dehnung als die Querproben; beim Flußeisen ist der Einfluß der Walzrichtung auf die Fertigkeit wechselnd, die Dehnung aber stets für die Querproben geringer. Am größten ist der Unterschied für Universaleisen, geringer für Formeisen und Bleche [31]–[33]. Ausglühen der Proben ist nur zulässig, wenn das Material in geglühtem Zustande Verwendung finden soll [20], [27], [33], [34].

2. Die Stabform. Ihr Einfluß auf das Versuchsergebnis setzt sich zusammen aus der Wirkung der stärkeren Stabköpfe und dem Einfluß der Größe des Querschnittes und der Meßlänge. Die stärkeren Stabköpfe behindern durch die auswärts gerichteten Seitenspannungen die Querschnittsverringerung und, da das Volumen des Stabes sich wenigstens bis zum Beginn der örtlichen Einschnürung beim Strecken nicht ändert, auch die Dehnung [10] und [35]. Theoretisch muß dieser Einfluß mit wachsender Entfernung von den Köpfen abnehmen, aber von beiden Köpfen aus durch Uebertragung von Querschnitt zu Querschnitt bis zur Stabmitte reichen; durch Messung wahrnehmbar bleibt er z.B. bei Stäben von 20 mm Durchmesser innerhalb etwa 30 mm Länge. Auf die Fertigkeit äußert sich dieser Einfluß bei dehnbarem Material derart, daß Stäbe von gleichem Querschnitt bei der Länge Null die größte Fertigkeit liefern. Unter ihnen besitzen Stäbe mit scharfem Einschnitt (Fig. 8) weniger Fertigkeit als solche mit eingearbeiteten Hohlkehlen nach Fig. 9. Dann nimmt die Fertigkeit mit wachsender Länge allmählich ab, bis sie schließlich für alle größeren Längen konstant wird [11], [29] und [36]–[39]. – Der Einfluß der Größe des Querschnittes und der Meßlänge veranlaßt, daß die Bruchdehnung bei gleicher Meßlänge mit dem Querschnitt wächst und umgekehrt bei gleichem Querschnitt mit wachsender Länge abnimmt. Der Grund liegt darin, daß die mit der Einschnürung verbundene, rein örtliche Dehnung gegenüber der gleichmäßig verteilten Dehnung bei kurze; Meßlänge mehr ins Gewicht fällt. Uebereinstimmende Werte erhält man nach Lebasteur und Marié [40] und nach Barba [10] mit verschiedenen Stabformen bei demselben Material dann, wenn die Stäbe in allen Teilen geometrisch ähnlich sind [41]. – Nach Bauschinger bleiben die ermittelten Dehnungswerte in allen Fällen vergleichbar, wenn sich die Meßlängen wie die Wurzeln aus den Querschnitten verhalten [42]. Er empfiehlt, die Stabformen an den Normalrundstab von 20 mm Durchmesser und 200 mm Meßlänge anzuschließen, d.h. stets die Meßlänge l = 200 · √(f : 314) = 11,3√f zu wählen. Für Stäbe, die in allen Teilen geometrisch ähnlich sein sollen, sind die Abmessungen dann nach den in Fig. 1 und 2 angegebenen Verhältnis werten zu berechnen [2], [43]–[45] und [53].

3. Die Lage des Bruches zur Meßlänge. Sobald der Bruch des Stabes nicht in der Mitte der Meßlänge, sondern in einer geringeren Entfernung von deren Enden erfolgt, fällt bei dehnbarem Material ein Teil der stärkeren örtlichen Dehnung, welche von der Einschnürung[1033] am Bruch herrührt, über die Meßlänge hinaus. Mißt man die Dehnung dann, wie es in der Regel geschieht, zwischen den Endmarken, so wird sie kleiner gefunden als beim Bruch in der Mitte. Das Ergebnis entspricht dann nicht mehr den Eigenschaften des Materials. Praktisch wahrnehmbar wird dieser Einfluß, sobald der Bruch außerhalb des mittleren Drittels der Meßlänge erfolgt. Stäbe mit derartig einseitig gelegenen Brüchen sind daher von der Messung der Dehnung zwischen den beiden Endmarken auszuschließen [28]. Um dem Uebelstande, daß auf diese Weise eine größere Zahl von Versuchen unbrauchbar wird, zu entgehen, hat man die Meßlänge vor dem Versuch durch Körner oder Strichmarken in 20 gleichgroße Stücke zu teilen (s. Fig. 10). Ist der Bruch nun z.B. in dem vierten Teilungsintervall, also zwischen Marke 3 und 4 erfolgt, so wird gemessen vom Bruch bis Marke 0 (3 Teile), ferner vom Bruch bis Marke 13 (10 Teile) und schließlich von Marke 6 bis 13 (7 Teile). Die Summe dieser drei Messungen entspricht der ursprünglichen Länge von 20 Teilen, also der vorgeschriebenen Meßlänge l, und die aus ihr sich ergebende Dehnung δ = 100 (Σ l_t – l) : l ist von der Lage des Bruches nicht beeinflußt. Vorausgesetzt wird hierbei, was erfahrungsgemäß zulässig ist, daß bei hinreichend langen Stäben die Dehnung zu beiden Seiten des Bruches gleichgroß ist [28]. Häufig pflegt man die Dehnungen an Hand der Unterteilungen für zwei verschiedene Längen zu ermitteln, und zwar nicht nur für je zehn, sondern auch noch für je fünf Teilungsintervalle zu beiden Seiten des Bruches. Der Vergleich beider Werte läßt dann erkennen, ob die Dehnung gleichmäßig über die ganze Länge verteilt ist, und besonders wie sie durch die örtliche Einschnürung beeinflußt wird. Die Unterteilungen werden entweder mit Körnerzirkel eingeschlagen oder mittels Schablonen (Fig. 11) und Reißnadel eingeritzt. Genauere Teilungen sind auf der Teilmaschine auszuführen.

4. Einfluß der Versuchsdauer [17], [46]–[48]. Bei jeder Laststeigerung ist eine gewisse Zeit erforderlich, damit der Probestab sich so weit dehnt, daß der Gleichgewichtszustand zwischen der äußeren Belastung und der inneren Materialspannung von neuem hergestellt ist. Innerhalb der Proportionalitätsgrenze sind die Dehnungen nur gering, die Zeit oder die Geschwindigkeit der Laststeigerung wird daher hier keinen meßbaren Einfluß ausüben. Er tritt aber hervor, sobald der Stab fließt, besonders bei Materialien mit Schaulinien nach Fig. 5a und 7. Am besten ist er zu erkennen bei Versuchen auf solchen Maschinen, die mit selbsttätiger Belastungsvorrichtung und mit Schaulinienzeichner ausgerüstet sind. Die Kraftordinaten sind dann um so größer, d.h. den gleichen Dehnungen entsprechen um so größere Belastungen, je größer die Arbeitsgeschwindigkeit beim Versuch ist. Bei gewissen Materialien, besonders bei Zink [49], äußert der Einfluß der Geschwindigkeit sich bis zum Bruch. Dann nimmt mit wachsender Geschwindigkeit die Fertigkeit zu, dagegen die Dehnung und in der Regel auch die Querschnittsverminderung ab. Um vergleichbare Ergebnisse zu erzielen, empfiehlt es sich daher, sämtliche Versuche mit gleicher Geschwindigkeit durchzuführen; geeignet ist hierzu die Geschwindigkeit von 1% der Meßlänge in der Minute.

Literatur: [1] Styffe, Knut, Die Festigkeitseigenschaften von Eisen und Stahl, Weimar 1870. – [2] Trescà, Sur l'écoulement des corps solides, Savant étrangers, Bd. XIII, S. 756. – [3] Vavra, Ueber einige Fließerscheinungen bei Zerreißversuchen von weichen Eisensorten, Prakt. Masch.-Konstr. 1892, S. 125. – [4] Unwin, On the Yield point of iron and steel etc., Proceedings of the Royal Society, vol. 57. – [5] Kirsch, Beiträge zum Studium des Fließens, Mitteil. a. d. Kgl. techn. Versuchsanstalten zu Berlin 1887, S. 69; 1888, S. 37 und 1889, S. 9. – [6] Martens, Untersuchungen mit Eisenbahnmaterial, ebend. 1890, Ergänzungsheft II. – [7] Kirkaldy, Strength and properties of materials, London 1891. – [8] Hartmann, Distribution des déformations sans les métaux soumis à des efforts, Paris 1896. – [9] Rudeloff, Untersuchungen über den Einfluß der Wärme auf die Festigkeit der Metalle, Mitteil. a. d. Kgl. techn. Versuchsanstalten zu Berlin 1893, S. 302. – [10] Barba, Etude sur la résistance des matériaux; Expériences à la traction, Mémoires de la Société des ingénieurs civils 1880. – [11] Considère-Hauff, Die Anwendung von Eisen und Stahl bei Konstruktionen, Wien 1888. – [12] The iron age 1890, S. 585. – [13] Zeitschr. d. Ver. deutsch. Ing. 1896, S. 569. – [14] Tetmajer, Einheitliche Nomenklatur für Eisen und Stahl, Eisenbahn 1884. – [15] Glasers Ann. f. Gew. u. Bauw. 1882, S. 137. – [16] Kick, Gesetz der proportionalen Widerstände, Leipzig 1885, S. 79. – [17] Jenny, Ueber Festigkeitsversuche und die dabei verwendeten Maschinen und Apparate, Wien 1878, S. 46. – [18] »Stahl und Eisen« 1882, S. 100. – [19] Wochenschr. d. Oesterr. Ing.- u. Arch.-Ver. 1882, S. 114. – [20] »Stahl und Eisen« 1883, S. 1 und 11. – [21] Civilingenieur 1884, S. 94 und 369. – [22] Wochenschr. d. Ver. deutsch. Ing. 1882, S. 48. – [23] Mitteil. a. d. Kgl. techn. Versuchsanstalten zu Berlin 1893, S. 33. – [24] Zeitschr. d. Ver. deutsch. Ing. 1891, S. 1089. – [25] Journ. of the Western Society of Engineers 1897, S. 589. – [26] Schweizerische Bauztg. 1884, S. 75. – [27] »Stahl und Eisen« 1884, S. 266. – [28] Beschlüsse der Konferenzen über einheitliche Untersuchungsmethoden, München 1893, S. 24. – [29] Mitteil. a. d. mech.-techn. Laboratorium München, Heft XIV, S. 159. – [30] »Stahl und Eisen« 1892, S. 15. – [31] Tetmajer, Mitteil. d. Anstalt zur Prüfung von Baumaterialien am eidgen. Polytechnikum in Zürich, Bd. 3, S. 186. – [32] Schweizerische Bauztg. 1892, Nr. 22 und 23. – [33] Oesterr. Zeitschr. für Berg- u. Hüttenw. 1885, S. 77. – [34] Glasers Ann. f. Gew. u. Bauw. 1885, S. 200. – [35] Barba und Duplaix, Sur les essais à la traction; Commission des méthodes d'essai des matériaux de construction, Bd. 3, 1895. – [36] Zeitschr. f. Bauw. 1866, S. 67. – [37] Oesterr. Zeitschr. f. Berg- u. Hüttenw. 1883, S. 557. – [38] Rudeloff, Beitrag zum Studium des Bruchaussehens zerrissener Stäbe, Baumaterialienkunde, Bd. 4, S. 85. – [39] Engineering 1897, Bd. 1, S. 187. – [40] Commission des méthodes d'essai[1034] 1894, Bd. 1, S. 120. – [41] Kick, Das Gesetz der proportionalen Widerstände, 1885. – [42] Mitteil a. d. mech.-techn. Laboratorium München, Heft XXI, S. 22. – [43] Barba, Etüde sur l'emploi de l'acier dans les constructions, Paris 1874. – [44] Marché, De la déformation permanente de l'acier, Comptes rendus de la Société des ingénieurs civils 1876, S. 474. – [45] Proceedings of the Inst, of civ. Eng. 1876, Bd. 66, S. 325. – [46] Dinglers Polyt. Journ. 1877, Bd. 223, S. 333 – [47] Gollner, Ueber die Untersuchung der Fertigkeit des Flußeisens, Technische Blätter. – [48] Dinglers Polyt. Journ. 1884, Bd. 251, S. 337. – [49] Mitteil. a. d. Kgl. techn. Versuchsanstalter zu Berlin 1889, Ergänzungsheft IV. – [50] Kgl. Pr. Akademie d. Wissenschaften, 1908, X, S. 210. – [51] Bach, Zum Begriff der Streckgrenze, Zeitschr. d. Ver. deutsch. Ing. 1904, S. 1040. – [52] Ders. Zur Kenntnis der Streckgrenze, ebend. 1905, S. 615. – [53] Martens, Materialienkunde für der Maschinenbau, Berlin 1898.

Rudeloff.

Fig. 1., Fig. 2.

Fig. 3., Fig. 4.

Fig. 5.

Fig. 6.

Fig. 7.

Fig. 8., Fig. 9.

Fig. 10.

Fig. 11.