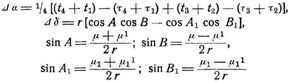Mikrometer
[426] Mikrometer, Instrumente zum Messen kleiner Größen jeder Art. Die hier in Betracht kommenden Einrichtungen dienen dazu, kleine Strecken auf Maßstäben, auf Winkelteilungen oder im Gesichtsfeld von Mikroskopen, Fernrohren u. dergl. noch genauer anzugeben, als es durch einfache Schätzung geschehen kann.
Je nach dem Gebrauch des Mikrometers hat man eine sehr große Zahl verschiedener Konstruktionen erdacht, die sowohl prinzipiell als auch konstruktiv verschieden sind. Handelt es sich um das Messen von Unterabteilungen von Maßstäben oder Kreisteilungen, so verwendet man dazu die Einrichtungen des Vernier oder Nonius (denn das ist streng genommen auch ein Mikrometer) oder die des Schraubenablesemikroskops1. Sollen kleine Strecken (Winkel) im Gesichtsfeld optischer Instrumente, namentlich im Fernrohr, gemessen werden, so benutzt man Netze von Spinnfäden oder Strichnetze auf Glas gezogen. Zu einer Messung ist es dann erforderlich, die Distanzen der einzelnen Fäden oder Striche in Winkelmaß zu kennen, diese Werte erhält man aus Durchgängen von Sternen, die dem Pol nahestehen, oder auch durch Messung mittels eines Theodoliten oder dergl. Zu einer wesentlich vollkommneren Einrichtung wird ein solches Mikrometer durch Hinzufügung eines sogenannten beweglichen Fadens. Dieses ist ein Faden, der durch eine Schraube äußerst nahe über die sogenannten festen Fäden um mittels dieser Schraube (Mikrometerschraube) meßbare Strecken hinweggeführt werden kann. Solche Mikrometer, die bei größeren Instrumenten auch zwei zueinander senkrechte Systeme von festen und beweglichen Fäden haben können, nennt man Schraubenmikrometer. Ist ein solches Schraubenmikrometer noch meßbar um die Achse des Fernrohres (Absehnslinie) drehbar, so können mittels desselben nicht nur lineare Entfernungen in zwei aufeinander senkrechten Koordinaten (Rektaszension und Deklination), sondern auch die Polarkoordinaten eines Objektes in Bezug auf ein andres (Entfernung und Positionswinkel) direkt gemessen werden.
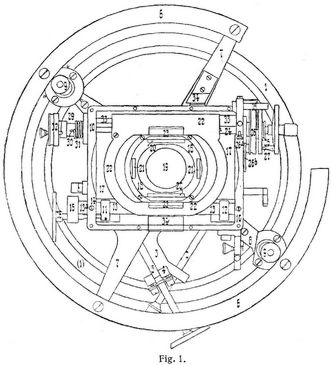
Zur Erläuterung der Einrichtung eines vollkommenen Schraubenmikrometers mag Fig. 1 dienen, die ein Repsoldsches Positionsmikrometer in schematischer Darstellung zeigt, nachdem die Okulardecke abgenommen ist. An der Grundplatte, die das Mikrometer mit dem Okularauszug des Fernrohrs verbindet, ist zunächst der Positionskreis 1 befestigt; derselbe trägt auf einem Silberstreifen die Gradteilung, welche die Drehung und damit den Positionswinkel (d.h. den Winkel zwischen Stundenkreis und Verbindungskreis der beiden Objekte) zu messen gestattet. An dem Klemmring 2, der die Drehung hemmt, ist der Arm 3 befestigt; dieser trägt das Lager 4 der Schraube 5, die mit ihrem Gewinde die Bewegung in Position vermittelt. Die Lupen 9 dienen zur Ablesung des Positionskreises. Mit den Speichen 7 und 8 in fester Verbindung steht eine Platte, welche die beiden Ansätze 11 und 12 trägt; letztere ragen durch Aussparungen in den Boden des eigentlichen Mikrometerkastens 10 hinein und nehmen in Durchbohrungen den Zylinder 13 auf, der darin in sehr exakter Führung gleiten kann. Derselbe ist durch die Schraube 14 mit dem Karten fest verbunden und ragt mit dem Ende 13a über denselben hinaus, wo der Ansatz 15 befestigt ist. In diesem hat wiederum die Schraube 16 ihr Muttergewinde, während sie durch die Wand des Mikrometerkastens frei hindurchgehend sich mit dem dünneren Ende auf den Ansatz 11 der Grundplatte stützt; durch sie ist also eine Bewegung des ganzen Mikrometers gegen die Grundplatte, gegen die der erstere mittels einer starken Feder angedrückt wird, möglich. Die untere Platte 17 des Mikrometerkastens trägt in ihrer Mitte einen ovalen Ring 18 mit so großer Oeffnung, daß auch bei starker Verschiebung die aus dem Fernrohr kommenden Lichtstrahlen noch frei hindurchgehen können. Der Ring ist oben plan abgeschliffen und dient zur Aufnahme der sogenannten festen Fäden (sie werden mit Schellack oder Wachs auf den schiefen Facetten 20 und 21 in der durch seine Linien vorher markierten Anordnung, die je[426] nach dem Gebrauch des Mikrometers verschieden gewählt wird, befestigt). Der an seiner einen Längskante mit einer nach unten gerichteten Verstärkung versehene Rahmen 22 trägt an seinen beiden Facetten 23 die beweglichen Fäden; er ist oben ganz genau plan geschliffen, und diese Ebene, auf der die beweglichen Fäden aufliegen, fällt fast genau mit der Ebene der festen Fäden zusammen, so daß die ersteren gerade noch ohne zu berühren über die letzteren hinweggeführt werden können. Diese Bewegung geschieht mittels der Mikrometerschraube 24, die auf der rechten Seite den Karten 10 frei durchsetzt und außerhalb desselben die Zähltrommeln trägt, und zwar 25 für die ganzen Umdrehungen und 26 für die Bruchteile derselben (Hundertstel direkt und Tausendstel durch Schätzung); die Uebertragung wird durch die Räder 26a und 26b vermittelt; die Ablesung geschieht an dem Index 28. Am linken Ende ruht diese Schraube auf der Stirnfläche eines Stahlzylinders, der bei 29 gelagert ist und mittels des Domes 30 und der Feder 31 in seiner Lage gesichert ist. Eine Bewegung des Zylinders kann im Umfange einer Umdrehung durch die Schraube mit geteilter Trommel 32 bewirkt werden, damit die Koinzidenzstellen zwischen festen und beweglichen Fäden zur Elimination etwa vorhandener periodischer Fehler der Mikrometerschraube verändert werden können.
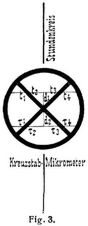
Andre Arten von Mikrometern sind solche mit feststehender Meßvorrichtung, wie die Ringmikrometer, Rhomben- und Kreuzstabmikrometer. Diese haben den Vorzug, daß man damit Beobachtungen im dunkeln Gesichtsfelde ausführen kann, während bei allen Fäden- oder Strichmikrometern wegen der Feinheit der letzteren irgendeine Beleuchtung entweder dunkler Fäden im hellen Felde oder heller Fäden im dunkeln Gesichtsfelde erforderlich ist. Ringmikrometer können bei allen Instrumenten mit Vorteil angewendet werden; das heute aber viel häufiger gebrauchte Kreuzstabmikrometer eignet sich nur für parallaktisch aufgestellte Instrumente.
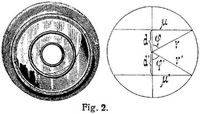
Fig. 2 stellt ein Fraunhofersches Ringmikrometer dar. Die Messung damit geschieht in der Weise, daß man die Ein- und Austrittszeiten zweier Gestirne an den Ring beobachtet (t1 t2 t3 t4 bezw. τ1 τ2 τ3 τ4). Die damit gewonnenen Sehnenlängen gestatten, einmal die Durchgangszeit durch den Stundenkreis des Mittelpunktes und anderseits den kürzesten Abstand (d und d') der scheinbaren Bahn des Gestirnes vom Mittelpunkt zu bestimmen, sobald man den angulären Durchmesser r des Ringes (hier den mittleren Durchmesser zwischen innerer und äußerer Kante) kennt. Es ist nämlich dann der Rektaszensionsunterschied der beiden Gestirne Δα und ihr Deklinationsunterschied Δδ durch die nachstehenden Ausdrücke leicht zu berechnen: wo
und die bezw. Werte von μ und μ1 die halben Verweilungszeiten aus den äußeren bezw. inneren Antritten an die Kanten des Ringes bedeuten.
Wählt man an Stelle des Ringes das Kreuzstabmikrometer (Fig. 3), so gestaltet sich die Rechnung viel einfacher, da die halbe Verweilungszeit direkt gleich dem Abstande des Weges des Gestirnes vom Kreuzungspunkt der beiden Lamellen ist. Eine weitere sehr wichtige Art der Mikrometer sind die Doppelbildmikrometer und darunter wieder das meistbenutzte die des Objektivheliometers. Dazu ist der Art. »Doppelbildmikrometer« zu vergleichen; dahin gehören auch die Wellmannschen Mikrometer. Für alle bei astronomischen Beobachtungen benutzten Mikrometer müssen bei der Auswertung der Resultate auch die Wirkungen der Refraktion und Parallaxe sowie bei bewegten Gestirnen (Planeten und Kometen) auch die der Eigenbewegung berücksichtigt werden. Dieserhalb muß aber hier auf die Lehrbücher der sphärischen Astronomie, die schon mehrfach genannt wurden, verwiesen werden.
Literatur: Das erste Schraubenmikrometer hat Gascoigne etwa um 1640 benutzt, dann folgten Auzout und Picard; die wesentlichsten Vervollkommnungen gab dem Instrumente Fraunhofer und heute werden von vielen mechanischen Präzisionswerkstätten gute Schraubenmikrometer angefertigt. In neuester Zeit hat man die sogenannten unpersönlichen Mikrometer nach Repsold besonders an Durchgangsinstrumenten (s.d.) eingeführt. Das Ringmikrometer ist angeblich von Lacaille zuerst in Form der Gesichtsfeldblende des Fernrohres angewendet worden. Im Anfang des 19. Jahrhunderts hat besonders der Bremer Arzt W. Olbers sehr viele und gute Kometenbeobachtungen damit angestellt. – Mikrometer, bei denen die Beugungserscheinungen der Lichtstrahlen zur Messung sehr kleiner Planeten- oder Mondscheiben benutzt werden, hat Bigourdan in Paris (Bulletin astronomique) angegeben. Beschreibungen der verschiedensten Arten von Mikrometern befinden sich in: Carl, Ph., Prinzipien der astronom. Instrumente. Ueber die Beleuchtung des Gesichtsfeldes ist zu vergleichen Littrow, K. v., Wiener Sitzungsberichte, Bd. 20 1856 und Bd. 40 1860. Die Theorie des Kreisbezw. Ringmikrometers gibt zunächst Bessel in Zachs Monatl. Korresp., Bd. 20; wieder abgedruckt in Bessels Abhandlungen, herausgegeben von Engelmann, Leipzig 1876. Die außerordentlich[427] große Literatur über Mikrometer zu astronomischem Gebrauch findet sich zusammengetragen in Ambronn, L., Handbuch der astronom. Instrumentenkunde, Bd. 2, S. 503 ff., daselbst sind fast alle Mikrometerkonstruktionen abgebildet; außerdem aber gibt Theorie und Gebrauch der Mikrometer in geradezu klassischer Behandlung mit vielen Abbildungen E. Becker in seiner Monographie über Mikrometer, Sonderabdruck aus »Handwörterbuch der Astronomie«, Breslau 1899.
Ambronn.
Buchempfehlung
Jean Paul
Vorschule der Ästhetik
Jean Pauls - in der ihm eigenen Metaphorik verfasste - Poetologie widmet sich unter anderem seinen zwei Kernthemen, dem literarischen Humor und der Romantheorie. Der Autor betont den propädeutischen Charakter seines Textes, in dem er schreibt: »Wollte ich denn in der Vorschule etwas anderes sein als ein ästhetischer Vorschulmeister, welcher die Kunstjünger leidlich einübt und schulet für die eigentlichen Geschmacklehrer selber?«
418 Seiten, 19.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Geschichten aus dem Sturm und Drang II. Sechs weitere Erzählungen
Zwischen 1765 und 1785 geht ein Ruck durch die deutsche Literatur. Sehr junge Autoren lehnen sich auf gegen den belehrenden Charakter der - die damalige Geisteskultur beherrschenden - Aufklärung. Mit Fantasie und Gemütskraft stürmen und drängen sie gegen die Moralvorstellungen des Feudalsystems, setzen Gefühl vor Verstand und fordern die Selbstständigkeit des Originalgenies. Für den zweiten Band hat Michael Holzinger sechs weitere bewegende Erzählungen des Sturm und Drang ausgewählt.
- Johann Karl Wezel Kakerlak oder die Geschichte eines Rosenkreuzers
- Gottfried August Bürger Münchhausen
- Friedrich Schiller Der Verbrecher aus verlorener Ehre
- Karl Philipp Moritz Andreas Hartknopfs Predigerjahre
- Jakob Michael Reinhold Lenz Der Waldbruder
- Friedrich Maximilian Klinger Geschichte eines Teutschen der neusten Zeit
424 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum