Paraboloïd

[413] Paraboloïd, Fläche zweiter Ordnung, wie Ellipsoid und Hyperboloid. Man unterscheidet: 1) Das elliptische P. (Fig. 1), das keine Geraden enthält.

Fig. 1. Elliptisches Paraboloid.

Am einfachsten ist das Rotationsparaboloid, das durch Rotation einer Parabel (s. d.) um ihre Achse, die dann auch die Achse des Rotationsparaboloids ist, entsteht.

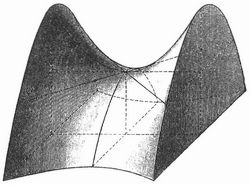
Fig. 2. Hyperbolisches Paraboloid.

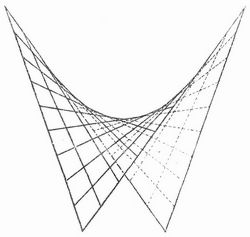
Alle zur Achse senkrechten Ebenen schneiden das Rotationsparaboloid in Kreisen, alle Ebenen durch die Achse schneiden es in kongruenten Parabeln. Ist das P. kein Rotationsparaboloid, so treten an die Stelle der Kreise ähnliche und ähnlich liegende Ellipsen und an die Stelle der kongruenten Parabeln lauter voneinander verschiedene, die aber alle die Achse des Paraboloids zur Achse haben. 2) Das hyperbolische P. (Fig. 2 u. 3), eine sattelförmige, geradlinige Fläche, bei der durch jeden Punkt zwei ganz auf der Fläche liegende Gerade gehen. In Fig. 2 ist ein von drei Ebenen abgeschnittenes Stück der Fläche dargestellt. Fig. 3 (S. 414) zeigt, wie die Geraden auf der Fläche liegen.[413]

Fig. 3. Hyperbolisches Paraboloid.

[414] Von einer Ebene wird die Fläche im allgemeinen in einer Hyperbel geschnitten, die auch in zwei[413] durch einen Punkt gehende Gerade ausarten kann; es gibt jedoch eine nicht auf der Fläche liegende Gerade, die Achse der Fläche, die so beschaffen ist, daß jede zur Achse parallele Ebene die Fläche in einer Parabel schneidet. Die einfachste Erzeugung der Fläche erhält man, wenn man eine Gerade sich so bewegen läßt, daß sie stets zwei nicht in einer Ebene liegende Gerade schneidet und dabei immer einer gewissen Ebene parallel bleibt.