Online-Bibliothek

Schubkurbelmechanismus

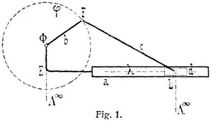
[821] Schubkurbelmechanismus besteht, wie in Fig. 1 schematisch dargestellt ist, aus vier Gliedern a, b, c, d, die in geschlossener Folge durch drei Drehpaarungen (s.d.) und eine Richtpaarung (s.d.) verbunden sind. Die Achsen Φ, F, L dieser drei Drehpaarungen sind parallel und senkrecht zur Zeichnungsebene. Die Richtpaarung ist in Fig. 1 durch die Führung des schlittenförmigen Gliedes d in dem geradlinigen Schlitz des Gliedes a vertreten. Der Schubkurbelmechanismus, den Reuleaux [1] Schubkurbelkette nennt, geht aus dem Kurbelmechanismus (s.d.) als spezieller Fall hervor, wenn von den vier Drehpaarungen desselben die eine durch eine Richtpaarung ersetzt, also die eine Achse Λ^∞ ins Unendliche verlegt wird (s. Mechanismen).

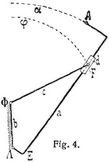
Wird eines der beiden Glieder a, d, die durch die Richtpaarung verbunden sind, z.B. das Glied a in Fig. 1, festgestellt, dann heißt der Schubkurbelmechanismus ein Schubkurbelgetriebe, und dieses ist ein zentrisches oder exzentrisches, je nachdem die Bahn λ des Punktes L durch oder nicht durch die Achse Φ geht, also die Strecke Φ E 0 ist. Das Schubkurbelgetriebe heißt ferner[821] ein rotierendes, wenn das Glied b um die feile Achse Φ rotiert, der Punkt F also den Kreis φ beschreibt, ein schwingendes, wenn das Glied b nur Schwingungen um die feste Achse Φ ausführen kann. Denken wir uns das Glied d festgestellt, dann kann das Glied c um die feste Achse L nur Schwingungen vollziehen und das Schubkurbelgetriebe ist dann ein schwingendes, bei dem das Schlitzglied a über dem festen Gliede d hin und her gleitet. Bei dem in Fig. 1 dargestellten exzentrischen rotierenden Schubkurbelgetriebe vollzieht der Schlitten d während einer Rotation der Kurbel b eine Schwingung, und diese schwingende Bewegung wird auch Kurbelschub genannt. Das rotierende Glieds heißt die Kurbel des Kurbelgetriebes und das Gliede heißt die Schubstange desselben. In Fig. 2 ist ein exzentrisches rotierendes Schubkurbelgetriebe in andrer Gestalt gezeichnet, bei dem die Richtpaarung durch die Hülse H des festgestellten Gliedes a und durch das in derselben gleitende stangenförmige Glied d gebildet ist. Am meisten wird in der Praxis das in Fig. 3 dargestellte zentrische Schubkurbelgetriebe angewendet, bei dem die Mittellinie λ des Schlitzes im festgestellten Gliede bezw. die Bahn des Achsenpunktes L durch die feste Achse Φ geht. Wenn bei einem Schubkurbelmechanismus in Fig. 4, dessen Richtpaarung beispielsweise aus einer Stange des Gliedes a und einer auf dieser gleitenden Hülse des Gliedes d gebildet ist, eines der Glieder b, c, etwa das schraffierte Glied b, festgestellt wird, dann heißt der Schubkurbelmechanismus ein Schleifkurbelgetriebe; und dieses wird ein exzentrisches oder zentrisches genannt, je nachdem die Strecke Λ E > 0 ist. Rotieren die beiden Glieder a, c um ihre festen Achsen Λ, Φ, so daß der Punkt F einen Kreis φ und ein beliebiger Punkt A des Gliedes a einen Kreis α durchläuft, dann heißt das Schleifkurbelgetriebe ein rotierendes. Wird dagegen in Fig. 4 das Glied c als fest betrachtet, dann rotiert das Glied b als Kurbel um die feste Achse Φ, und das Glied d vollzieht Schwingungen um seine feste Achse F. In diesem Falle wird das Schleifkurbelgetriebe ein schwingendes genannt. In Fig. 5 und 6 sind zwei zentrische Schleifkurbelgetriebe dargestellt, bei welchen die Richtpaarung durch einen prismatischen Schlitz des Gliedes a bezw. eine Schleife und einen in dieser gleitenden Schlitten gebildet ist. Das Schleifkurbelgetriebe in Fig. 5 ist ein rotierendes, weil die Punkte A, F bezw. die Kreise α, φ durchlaufen. In Fig. 6 vollzieht während jeder Umdrehung der Kurbel c das Glied a eine hin und her gehende Schwingung um die feste Achse Λ. Während also der Punkt F der Kurbel den Kreis φ durchläuft, bewegt sich der Punkt A des Gliedes a auf den Kreisbogen A' A A'' hin und her, und das Schleifkurbelgetriebe ist demnach ein schwingendes. In der schleifenförmigen Gestaltung wird das Schleifkurbelgetriebe am meisten angewendet und wird deshalb auch Kurbelschleife (s.d.) genannt. Die Konstruktionen der Geschwindigkeiten sowie der Beschleunigungen der Punkte der bewegten Glieder bei den Schubkurbel- und den Schleifkurbelgetrieben wird in der Kinematik gelehrt [2].

Literatur. [1] Reuleaux, Theoretische Kinematik, Braunschweig 1875, S. 324. – [2] Burmester, L., Lehrbuch der Kinematik, Leipzig 1888.

Burmester.

Fig. 1.

Fig. 2., Fig. 3., Fig. 5.

Fig. 4.

Fig. 6.