Online-Bibliothek

Beschleunigung

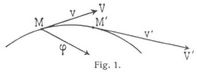
[715] Beschleunigung (Acceleration). Die Geschwindigkeit ν der Bewegung eines Punktes M (Fig. 1) hat die Richtung der Tangente an die Bahn in M und ändert sich mit der Zeit nach Größe, Richtung und Lage. Sie ist eine[715] gerichtete Größe. Ihr Differentialquotient nach der Zeit heißt Beschleunigung und ist gleichfalls eine gerichtete Größe.

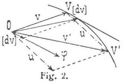
Von der Lagenänderung des bewegten Punktes absehend, kann man fragen, wie die Aenderung der Geschwindigkeit nach Größe und Richtung erfolgt. Zieht man von irgend einem Punkte O des Raumes Radiusvektoren OV gleich und parallel den Geschwindigkeiten υ, so folgt ein so veränderlicher Radiusvektor OV der Bewegung des Punktes M und beschreibt dessen Endpunkt V eine Kurve, Hamiltons Hodograph der Geschwindigkeiten, die sehr geeignet ist, die Aenderung der Geschwindigkeit υ nach Größe und Richtung zu beurteilen (Fig. 2). Sind υ = OV und υ' = OV' die Geschwindigkeiten von M, entsprechend den Zeiten t und t + Δt, so kann υ' als Resultante von ν und einer andern Komponente Ou = Δυ dargestellt werden, d.h. als die geometrische Summe [υ'] = [υ] + [Δυ], so daß [Δυ] die Größe darstellt, die zur Geschwindigkeit ν der Zeit t hinzutreten muß, um diese in die Geschwindigkeit υ' zur Zeit t + Δt nach Größe und Richtung überzuführen. (Die Klammern deuten, daß die eingeschlossenen Größen als gerichtete zu verstehen und zu addieren sind.) Nimmt Δt ohne Ende ab und verschwindet es als das Zeitdifferential dt, so nimmt auch [Δυ] ohne Ende ab und verschwindet als geometrisches Differential [dυ] von [υ], dem die Richtung der Tangente an den Hodographen in V zukommt, und das Bogendifferential VV' dieser Kurve stellt diese unendlich kleine Aenderung der Geschwindigkeit [υ] nach Größe und Richtung zugleich dar. Man nennt das geometrische Differential der Geschwindigkeit [υ] die Elementarbeschleunigung von [υ]. Die Elementarbeschleunigung ist eine unendlich kleine gerichtete Größe. Dividiert man dieselbe mit dem Zeitelemente dt, d.h. bildet man die Komponente, die zur Geschwindigkeit [υ] hinzutreten würde, wenn der Prozeß ihrer Aenderung eine volle Zeiteinheit in derselben Richtung fortdauern würde, wie er im Zeitelement besteht, so erhält man die geometrische Ableitung oder den geometrischen Differentialquotienten der Geschwindigkeit [υ] des Punktes M zur Zeit t. Die geometrische Ableitung der Geschwindigkeit heißt die Beschleunigung der Geschwindigkeit υ, oder auch die Beschleunigung der Bewegung des Punktes M zur Zeit t. Bezeichnet man dieselben nach Größe mit φ und nach Größe und Richtung mit [φ], so hat man für sie [φ] = [dυ]/dt und für die Elementarbeschleunigung [dν] = [φ] dt.

Die Beschleunigung fällt stets in die Ebene zweier aufeinander folgenden Tangenten der Bahn, d.h. in die Schmiegungsebene derselben. Für ebene Kurven fallen alle Schmiegungsebenen in eine, die Ebene der Kurve selbst, zusammen.

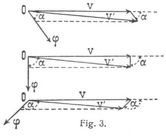
Der Hodograph gibt ein sehr deutliches Bild von der Veränderung der Geschwindigkeit durch den Hinzutritt der Elementarbeschleunigung. Bildet nämlich die Tangente des Hodographen, d.h. die Richtung der Beschleunigung mit der Tangente der Bahn, d.h. mit der Richtung der Geschwindigkeit oder mit dem Radiusvektor des Hodographen einen spitzen, rechten oder stumpfen Winkel α (Fig. 3), so wächst in dem betreffenden Moment die Geschwindigkeit, bleibt einen Moment stationär oder nimmt ab und umgekehrt. Für die gleichförmige Bewegung von M ist ν konstant und der Hodograph mithin eine sphärische Kurve; für die geradlinige Bewegung ist der Hodograph eine Gerade, die sich für konstante Geschwindigkeit auf einen Punkt reduziert. Für die geradlinige Bewegung ändert die Geschwindigkeit bloß ihre Größe, nicht aber ihre Richtung, OV, VV' und OV' (Fig. 4) fallen zusammen in der Richtung der Geschwindigkeit, und es wird die Elementarbeschleunigung VV' = dυ, d.h. gleich dem gewöhnlichen Differentiale von ν nach Größe und die Beschleunigung φ = dυ/dt. Projiziert man daher den Punkt M während seiner Bewegung auf eine Achse, so folgt aus dem Satze, daß die Geschwindigkeit υ_x für die Bewegung der Projektion m die Projektion der Geschwindigkeit υ von M ist, für die Beschleunigung der Projektionsbewegung φ_x = dυx/dt und da υx = dx/dt ist, φx = d²x/dt², d.h. so wie die Geschwindigkeit der Projektionsbewegung des Punktes M auf eine Achse (beispielsweise die x-Achse eines Koordinatensystems) der erste Differentialquotient der dieser Achse entsprechenden Koordinate x ist, so stellt der zweite Differentialquotient d²x/dt² die Beschleunigung der Projektionsbewegung dar. Zugleich bemerkt man, daß, wenn λ den Winkel bedeutet, den VV' mit der Achse bildet, dυ_x = dυ ∙ cos λ, also dυx/dt = dυ/dtcosλ, d.h. φx = φ cos λ wird. Es ist demnach die Beschleunigung der Projektionsbewegung gleich der Projektion der Beschleunigung der Hauptbewegung auf die Achse. Dieser Satz besteht auch für die Projektion der Bewegung von M auf eine Ebene, wie man erkennt, indem man das Dreieck OVV' auf dieselbe projiziert. Projiziert man die Bewegung von M auf die drei Achsen eines rechtwinkligen Koordinatensystems, so[716] hat man daher für die Geschwindigkeiten und Beschleunigungen der drei Projektionsbewegungen die Gleichungen:

Sind φ_x, φ_y, φ_z als Funktionen der Zeit t oder der Koordinaten x, y, z des Punktes M oder allgemein als Funktionen von t, x, y, z, dx/dt, dy/dt, dz/dt gegeben, so heißen die drei letzten Gleichungen die Differentialgleichungen der Bewegung des Punktes M, und man kann aus ihnen durch Integration die Koordinaten und Geschwindigkeiten als Funktionen der Zeit finden, wobei sechs Integrationskonstante eingehen. Diese sechs Konstanten werden durch die Koordinaten des Punktes M zur Zeit t = 0 und die Komponenten der Geschwindigkeit desselben entsprechend t = 0 bestimmt.

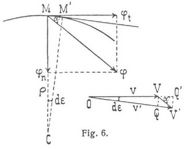
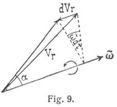
Nach der Theorie der Strecken kann die Beschleunigung φ auf verschiedene Arten in Komponenten zerlegt und aus ihnen gebildet werden. So kann sie aus den Projektionsbeschleunigungen φ_x, φ_y, φ_z zusammengesetzt werden, ähnlich wie die Geschwindigkeit ν aus den Projektionsgeschwindigkeiten gebildet werden kann. Eine besonders wichtige Zerlegung von φ in zwei Komponenten ist die Zerlegung derselben in die Tangential- und Normalbeschleunigung. Ist α der Winkel der Beschleunigung φ gegen die Tangente der Bahn oder gegen die Richtung der Geschwindigkeit, so sind φt = φ cos α und φn = φsinα die Tangentialkomponente und Normalkomponente derselben (Fig. 6). Beschreibt man aus dem Pole O des Hodographen mit υ und υ' zwei Kreisbogen VQ und V'Q', so ergibt sich sofort

wo dε den Kontingenzwinkel VOV' bezeichnet. Hiermit werden

Mit Rücksicht darauf, daß der Krümmungshalbmesser in M gleich dem Bogenelemente ds, dividiert durch den Kontingenzwinkel: ρ = ds/dε und υ = ds/dt ist, ergeben sich für die Normalkomponente φn durch Elimination von ds oder ν nach zwei andre Formen, so daß man überhaupt an Formeln zur Disposition hat:

Die Zerlegung der Beschleunigung in zwei Komponenten, von denen die eine die Richtung der Geschwindigkeit, die andre die der Normalen hat, ist besonders wertvoll deswegen, weil sie den Anteil, den die Beschleunigung an der Richtungsänderung der Geschwindigkeit hat, von dem Anteile trennt, den sie an der Aenderung von deren Größe nimmt. Die Formel für die Tangentialbeschleunigung φt enthält nämlich nichts, was sich auf die Richtungsänderung der Tangente oder auf die Krümmung der Bahn bezieht, während der Ausdruck

solche Elemente zeigt, nämlich den Krümmungshalbmesser und den Kontingenzwinkel. Die Tangentialbeschleunigung φt ändert daher bloß die Größe, die Normalbeschleunigung aber die Richtung von υ. Die Normalbeschleunigung φn führt auch den Namen der Zentripetalbeschleunigung, weil ihr Sinn auf den Krümmungsmittelpunkt hinweist, nach dem zu die Tangente abbiegt.

Für geradlinige Bahnen ist φn = 0 daher φ = φt =dυ/dt, α = σ, ρ = ∞, für konstante υ, d.h. für gleichförmige Bewegung ist φ_τ = 0, also φ = φ_r = υ²/ρ, α = ¹/₂π; für die geradlinige gleichförmige Bewegung ist φ = φ_r = φ_n = 0.

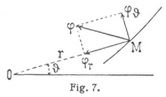
Eine andre Zerlegung der Beschleunigung einer ebenen Bewegung in zwei Komponenten φr, φδ ist die Zerlegung nach dem Radiusvektor r eines Polarkoordinatensystems der r, ϑ und senkrecht zu diesem (Fig. 7). Man findet für die Komponenten:

δr = [d²r/dt² – r(dδ/dt)²],

φ_δ = 2 · dr/dt · dδ/dt + r · d²δ/dt² = 1/r · d/dt (r² · dδ/dt).

Indem man die beiden Gleichungen

dυ/dt = φt, υ = ds/dt[717]

für die Tangentialbeschleunigung und die Geschwindigkeit behufs Elimination von dt durch Multiplikation miteinander kombiniert, ergibt sich:

d · 1/2 ν² = φt · ds.

Das Produkt φt ∙ ds aus der Tangentialkomponente der Beschleunigung und dem Bogenelemente ds der Bahn des Punktes nennt man die Elementararbeit der Beschleunigung φ längs ds. Das Integral der Elementararbeit, d.h. die Summe aller Elementararbeiten, ausgedehnt über einen Bogen s – s₀ (Fig. 8) heißt die totale Arbeit oder die Arbeit der Beschleunigung längs des; Weges s = s₀. Sind υ₀, υ die Werte der Geschwindigkeiten in den Punkten M_o, M der Bahn, deren Abstände von einem willkürlich wählbaren Punkte O derselben s₀ und s sind, so erhält man durch Integration

wobei d den Winkel zwischen Beschleunigung und Geschwindigkeit bedeutet. Demnach wird die totale Arbeit der Beschleunigung φ längs des Weges s – s₀ dargestellt durch die Aenderung ¹/₂υ² – ¹/₂υ²₀, die das halbe Geschwindigkeitsquadrat beim Uebergange des Punktes M von M_o nach M erleidet.

Beschleunigung bei der zusammengesetzten und bei der Relativbewegung.

Ein Punkt M möge sich auf einer Kurve (Bahn) bewegen, die ihrerseits eine Bewegung, die auch mit Gestaltsänderung verbunden sein mag, ausführt. Wir wollen die Lage des Punktes M durch eine vom Anfangspunkt des Koordinatensystems auslaufende gerichtete Größe [r] bestimmen. Diese gerichtete Größe [r] denken wir uns zunächst von »zweierlei« Zeiten t und τ abhängig, also [r] = f(t, τ). Ist τ konstant, so ist die Kurve, auf der sich der Punkt bewegt, in Ruhe und t ist die veränderliche Zeit für die Bewegung des Punktes auf der festen Kurve. Ist t konstant und τ veränderlich, so erhalten wir den Weg, den ein mit der Kurve fest verbundener Punkt bei ihrer Bewegung beschreibt. Für die zusammengesetzte Bewegung des Punktes M ist t = τ zu setzen. Die Veränderung von [r] als gerichtete Größe aufgefaßt wird:

Wird für die wirkliche Bewegung dτ = dt gesetzt und mit dt dividiert, so erhält man:

Bezeichnen wir die Geschwindigkeit der zusammengesetzten Bewegung des Punktes mit [υ], jene auf der ruhenden Kurve mit [υ_r] und jene des Kurvenpunktes mit [υf], so sagt die Gleichung [υ] = [υ_r] + [υf] daß erstere die Resultante aus letzteren ist. Um zu den Beschleunigungen zu kommen, betrachten wir die Veränderung von [υ]:

Setzen wir für die wirkliche Bewegung wieder dτ=dt und dividieren wir mit dt, so erhalten wir:

Hiernach stellt sich die Beschleunigung [7] der zusammengesetzten Bewegung eines Punktes als Resultante dreier Komponenten dar. Die erste [φ_r] ist die Beschleunigung des Punktes auf der ruhend gedachten Bahn, die zweite [φf] die Beschleunigung des auf der Bahn ruhend gedachten Punktes infolge der Bewegung der Bahn, die dritte [φc] heißt die Coriolissche Beschleunigung oder zusammengesetzte Zentripetalbeschleunigung. Sie rührt von der Aenderung der Geschwindigkeit [υr] durch die Bewegung der Bahn her: Es ist nämlich

Ist die Bewegung der Bahn durch eine Drehung mit der Winkelgeschwindigkeit ω um eine Achse, die den Winkel α mit der Geschwindigkeit [φr] bildet, veranlaßt, so fleht die Veränderung, die [υr] in der Zeit dτ erfährt, senkrecht zur Achsenrichtung und ist gleich ω d τ υ_r sin α. Hiernach steht [φc] senkrecht zur Drehachse und zu Geschwindigkeit, während sein absoluter Betrag der Wert φc = 2 ω υ r sin α ist.

Die zusammengesetzte Bewegung des Punktes M kann man als absolute Bewegung auffassen, die Bewegung desselben Punktes auf der Bahn als relative und die Bewegung der Bahn selbst als Führungsbewegung. Es ergibt sich dann die absolute Beschleunigung [φ] eines Punktes als geometrische Summe (Resultante) der relativen Beschleunigung [φr], der Führungsbeschleunigung [φf] und der Coriolisschen oder zusammengesetzten Zentripetalbeschleunigung [φc].

Weiteres über die Beschleunigung, namentlich über die Beschleunigung der Punkte im unveränderlichen Punktsystem s. Beschleunigungszentrum. Weitere Ausführungen über die Beschleunigungen s. [1].

Literatur: [1] Schell, Theorie der Bewegung und der Kräfte, Leipzig 1879–80, 2. Aufl., Bd. 1, s. 312 u. ff.

(Schell) Finsterwalder.

Fig. 1.

Fig. 2.

Fig. 3.

Fig. 4.

Fig. 5.

Fig. 6.

Fig. 7.

Fig. 8.

Fig. 9.