Ovāl
[265] Ovāl (neulat., »eirund«), jede in sich zurücklaufende ebene Kurve, deren Gestalt, wie die der Ellipse, an die Form des Eies erinnert. Insbesondere nennt man O. (Korblinie, Korbbogen) eine ebene krumme, aus Kreisbogen zusammengesetzte Linie dieser Art, die bei Konstruktion von Gewölbebogen angewendet wird (vgl. Bogen).
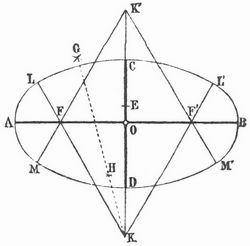
Eine der vielen Arten, solche Linien zu zeichnen, ist folgende (s. Figur): Sind AB und CD die beiden Achsen, die sich im Mittelpunkt O rechtwinklig halbieren, so nehme man auf der kleinern Halbachse OC den Punkt E willkürlich an, mache AF = F´B = CE und schlage um E und F mit willkürlicher, aber gleichgroßer Zirkelöffnung Bogen, die sich in G und H schneiden; ziehe dann die Gerade GH, die CD oder die Verlängerung dieser Achse in K schneidet, und trage nun OK´ = OK ab. Die Punkte K und K´ werden dann mit F und F´ durch gerade Linien verbunden, die man noch über F und F´ hinaus verlängert, und nun beschreibt man mit der Öffnung KC = K´D um K den Bogen LL´, um K´ den Bogen MM´ sowie zuletzt um F und F´ mit der Öffnung FL = F´L´ die Bogen LAM und L´BM´. Vgl. Behse, Die praktischen Arbeiten und Baukonstruktionen des Maurers und Steinhauers, § 53 (6. Aufl., Weim. 1893); Küpper in Grunerts »Archiv der Mathematik«, Bd. 28, S. 256; Delabar, Anleitung zum Linearzeichnen (10 Hefte, Freiburg i. Br. 1895).
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum