Kurve

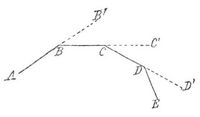
[872] Kurve (lat.), in der Geometrie zunächst eine krumme Linie im Gegensatze zur Geraden, doch rechnet man, wenn man von Kurven überhaupt spricht, gewöhnlich auch die geraden Linien dazu, indem man sie als Kurven betrachtet, deren Krümmung (s. d.) gleich Null ist. Den Übergang von der geraden Linie zur krummen (also zur K. im eigentlichen Sinne) vermittelt am besten die gebrochene Linie; eine solche erhält man, wenn man eine Anzahl von Punkten A, B, C, D..., von denen keine drei aufeinanderfolgenden in gerader Linie liegen, der Reihe nach durch die Geradenstücke AB, BC, CD... verbindet (Fig. 1).

Fig. 1.

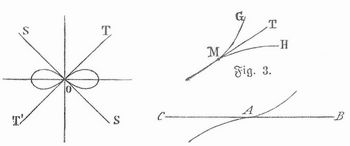
Denkt man sich einen Punkt, der, von A ausgehend, die gebrochene Linie ABC... durchläuft, so ändert dieser in jedem der Punkte B, C, D... plötzlich die Richtung, in der er sich bewegt, indem erz. B. in B nicht auf der Verlängerung BB' von AB fortgeht, sondern auf der Geraden BC, die mit BB' einen gewissen Winkel B'BC bildet. Denkt man sich nun, daß die Geradenstücke AB, BC... und mit ihnen die Winkel B'BC, C'CD... immer kleiner und kleiner werden und schließlich unter jede meßbare Größe herabsinken, so geht die gebrochene Linie in eine K. über; ein Punkt, der diese K. durchläuft, ändert die Richtung seiner Bewegung nicht wie bei der gebrochenen Linie von Zeit zu Zeit plötzlich oder sprungweise (diskontinuierlich), sondern er ändert sie fortwährend, aber in jedem Augenblick nur ganz unmerklich, er ändert sie, wie man sagt, stetig oder kontinuierlich. In jedem Punkte P der K. gibt es eine Gerade, die zu P gehörige Tangente der K., die angibt, in welcher Richtung sich ein die K. durchlaufender Punkt in dem Augenblick bewegt, wo er durch P hindurchgeht. Kurven, die ganz in einer Ebene enthalten sind, heißen eben, wie z. B. die Kegelschnitte (s. d.), jede andre K. ist eine Raumkurve und heißt doppeltgekrümmt oder auch gewunden, wie die Schraubenlinie (s. d.). Bestimmt man die Punkte durch Koordinaten (s. d.), so wird eine ebene K. durch eine Gleichung zwischen zwei Koordinaten dargestellt, eine Raumkurve durch zwei Gleichungen zwischen drei Koordinaten; im zweiten Falle stellt jede dieser Gleichungen eine Fläche dar, und die K. ist der Schnitt dieser beiden Flächen. Eine K. heißt algebraisch oder transzendent je nach der Beschaffenheit der betreffenden Gleichungen (s. d.), z. B. sind die Kegelschnitte algebraisch, die Zykloide (s. d.) und die Schraubenlinie transzendent. Die ebenen algebraischen Kurven teilt man ein in Ordnungen und Klassen. Die Ordnung einer solchen K. ist gleich dem Grade der Gleichung, durch welche die K. dargestellt wird, oder, was auf dasselbe hinauskommt, gleich der Zahl der Punkte, in denen die K. von einer beliebigen Geraden geschnitten wird; die Klasse der K. ist die Zahl der Tangenten, die von einem beliebigen Punkte der Ebene aus an die K. gezogen werden können. Die Kegelschnitte z. B. sind Kurven zweiter Ordnung und zweiter Klasse; im allgemeinen ist eine ebene K. n-ter Ordnung von n(n-1)-ter Klasse. Die Ordnung einer Raumkurve ist die Zahl der Punkte, in denen die K. von einer beliebigen Ebene geschnitten wird. – Kurven mit Mittelpunkt sind solche, deren Punkte paarweise zu einem bestimmten Punkte (dem Mittelpunkt oder Zentrum der K.) symmetrisch liegen (s. Symmetrie), dazu gehören z. B. Kreis, Ellipse und Hyperbel (s. d.). Über die Länge einer K. s. Länge. Auf den ebenen algebraischen Kurven, deren Ordnung größer als zwei ist, gibt es ausgezeichnete, sogen. singuläre Punkte. Z. B. kann ein Punkt Doppelpunkt der K. sein; dann gehen durch ihn zwei Äste der K. hindurch, zu deren jedem eine Tangente gehört, und die K. bildet eine Schleife (Fig. 2).

Fig. 2., Fig. 3. Fig. 4. Fig. 2. Lemniskate, O der Doppelpunkt mit den beiden Tangenten SOS' und TOT'. – Fig. 3. M Spitze, ein Doppelpunkt, in dem die beiden Tangenten T an die beiden Zweige MG und MH zusammenhalten. – Fig. 4. Wendepunkt bei A.

Zieht sich diese Schleife zu einem Punkt zusammen, so verwandelt sich der Doppelpunkt in eine Spitze, von der zwei einander berührende Äste der K. ausgehen (Fig. 3). Ein Wendepunkt ist dadurch ausgezeichnet, daß die zugehörige Tangente die K. in der zweiten Ordnung berührt (s. Kontakt) und im Wendepunkte durch die K. hindurchgeht (Fig. 4, auch in Fig. 2 hat jeder der beiden durch O gehenden Äste der Lemniskate in O einen Wendepunkt). Ist n die Ordnung der K., a die Anzahl der Doppelpunkte, k die der Spitzen, so ist die Zahl p = ¹/₂(n-1)(n-2)-δ-k niemals negativ und heißt das Geschlecht der K. Eine K. vom Geschlecht p kann höchstens aus p+1 untereinander nicht zusammenhängenden Teilen oder, wie man sagt, Zügen bestehen. Näheres über die singulären Punkte etc. findet man in Clebschs »Vorlesungen über Geometrie«, Bd. 1 (hrsg. von Lindemann, Leipz. 1876) und in Salmons »Analytischer Geometrie der höhern ebenen Kurven« (deutsch von Fiedler, 2. Aufl., das. 1882). Eine Übersicht über alle bekannten ebenen Kurven gibt: Loria, Spezielle algebraische und transzendente ebene Kurven (deutsch von Schütte, Leipz. 1902). Über Doppelkurven s. Oberflächen.