Online-Bibliothek

Bodenplastik [2]

[86] Bodenplastik. Wie überhaupt in einem Punkte einer beliebigen Fläche, so haben wir auch in einem Punkte der wirklichen Erdoberfläche die Art der Krümmung der Fläche in ihm zu beachten.

Man unterscheidet zwei Arten der Krümmung, die eilipsoidische und die hyperboloidische. Denken wir uns im betrachteten Punkte der Fläche eine Normale errichtet und durch diese unendlich viele Ebenen gelegt, so ergibt jede dieser Ebenen einen Normalschnitt der Fläche, der im betrachteten Punkte eine gewisse Krümmung besitzt. Das in Betracht kommende kleine, dem Punkte benachbarte Stück des Normalschnittes können wir uns durch einen kleinen Kreisbogen ersetzt denken; sein Mittelpunkt ist der Krümmungsmittelpunkt, sein Halbmesser der Krümmungshalbmesser des Normalschnitts im betrachteten Punkte. Liegen nun die Krümmungsmittelpunkte aller Normalschnitte an derselben Seite der Fläche, so ist diese im betrachteten Punkte ellipsoidisch gekrümmt; unter den Normalschnitten gibt es jetzt zwei, die sogenannten Hauptschnitte, denen ein Maximum und ein Minimum des Krümmungsradius entspricht; sie sind stets aufeinander rechtwinklig. Liegen aber die Krümmungsmittelpunkte der Normalschnitte an verschiedenen Seiten der Fläche, so ist diese im betrachteten Punkte hyperboloidisch gekrümmt; zwei aufeinander senkrechte Normalschnitte sind jetzt entgegengesetzt gekrümmt, und es gibt zwei aufeinander senkrechte Hauptschnitte, denen Minimalwerte des Krümmungsradius, also schärfste Krümmungen in dem einen und dem andern Sinne entsprechen. – Auf der Erdoberfläche ist beispielsweise der höchste Punkt einer Bergkuppe, der tiefste Punkt eines Wasserbeckens ein Punkt ellipsoidischer Krümmung, ein in einem »Sattel« liegender Punkt hingegen ein Punkt hyperboloidischer Krümmung. – In einem Punkte ellipsoidischer Krümmung hat die Tangentenebene mit der Fläche nur ein Flächenelement gemein; die in einem Punkte hyperboloidischer Krümmung an die Fläche gelegte Tangentenebene aber schneidet die Fläche in einer Kurve, die in dem angenommenen Punkte sich selbst schneidet, also eine Schleife bildet.[86]

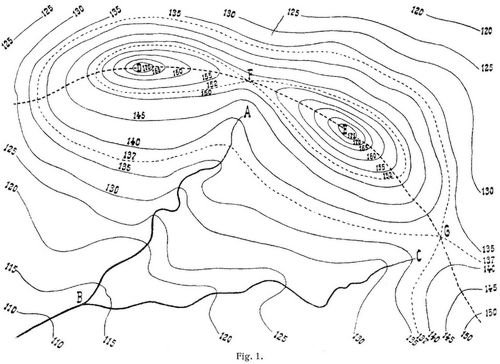
Die Darstellung der Bodenplastik auf Landkarten erfolgt am besten durch die Eintragung von Höhenkurven oder Isohypsen. Man versteht darunter die Schnittlinien der Erdoberfläche mit in gleichen vertikalen Abständen angenommenen Horizontalebenen. Dabei ist von der Krümmung der Erdkugel abgesehen, was, da es sich hier stets nur um die Darstellung kleiner Teile der Erdoberfläche handelt, zulässig erscheint. Die Höhenkurven lassen einen unmittelbaren Schluß auf die Stärke der Neigung der Fläche gegen die Horizontalebene im betrachteten Punkte zu; je näher die Kurven aneinander rücken, um so größer ist die Neigung. – Die Fig. 1 zeigt den Verlauf der Höhenkurven, die in lotrechten Abständen von 5 m angenommen wurden, in einer gedachten Hügellandschaft im Maßstabe 1 : 5000; wir sehen zwei Wasserläufe A B und C B, die sich in B vereinigen, ferner zwei Gipfel D und E und zwei Einsattelungen F und G. Die Wasserläufe geben den Verlauf der Täler an; sie schneiden die Höhenkurven rechtwinklig, und zwar jede Kurve da, wo sie am schärfsten gekrümmt ist; die Abstände der Kurven voneinander sind hier am größten – der Wasserlauf stellt also eine Linie schwächsten Gefälles dar. Durch die Punkte D, F, E, G geht die Wasserscheide; auch sie ist eine Linie schwächsten Gefälles, die die Höhenkurven rechtwinklig und in größten Abständen schneidet. Die Punkte F und G, die relativ tiefsten Punkte der Wasserscheide sind Pässe, die in benachbarte Täler hinüberführen; wir können den Paß mathematisch als einen Punkt hyperboloidischer Krümmung mit horizontaler Tangentenebene definieren. Legen wir durch den Punkt F oder G selbst eine Horizontalebene – sie ist die soeben erwähnte Tangentenebene –, so ergibt sie eine Höhenkurve, die im Punkte F oder G sich selbst schneidet; beide Kurven sind in die Zeichnung gestrichelt eingetragen. – Das Gebiet eines Wasserlaufes – Bach-, Fluß-, Stromgebiet – ist dasjenige Stück der Erdoberfläche, dessen Meteorwasser durch den Wasserlauf abgeführt wird; es wird durch die Wasserscheiden begrenzt.

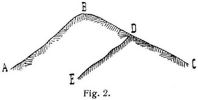
Durch jeden Punkt der Oberfläche geht eine Kurve stärksten Gefälles, die alle Höhenkurven rechtwinklig schneidet; sie gibt den Weg an, den ein in diesem Punkte auffallender Wassertropfen beim Abfließen einschlägt. Zu diesen Kurven stärksten Gefälles gehören auch die Wasserläufe oder Talwege und die Wasserscheiden, Wenn diese Linien oben als Linien schwächsten Gefälles bezeichnet wurden, so hat dies den Sinn, daß sie unter den Linien stärksten Gefälles diejenigen sind, denen das schwächste Gefälle zukommt. Ziehen wir nicht nur das an der Oberfläche ablaufende, sondern auch das versickernde Wasser in Betracht, so werden durch geologische Verhältnisse manchmal Veränderungen der rein geometrischen Wasserscheiden bewirkt. Es sei (Fig. 2) A B C ein durch die Wasserscheide gelegter Vertikalschnitt, B also ein Punkt der geometrischen Wasserscheide; in einer gewissen Tiefe unter der Oberfläche befinde sich eine undurchlässige Schicht D E; dann wird für das Sickerwasser die Wasserscheide nicht durch B, sondern durch D gehen.

Reliefkarten stellt man am besten dadurch her, daß man aus Brettchen von gleicher Dicke nach der Form der Höhenkurven Schichten aussägt, diese aufeinander leimt und die Stufen mit Ton oder Gips ausfüllt. Die beliebten Reliefkarten größerer Gebiete mit Ueberhöhung – der Maßstab für die Höhen ist viel größer als der für die horizontale Erstreckung – sind pädagogisch äußerst bedenklich, da sie in den Schülern ganz verkehrte Vorstellungen von den Neigungen erwecken. Immerhin sind sie wenigstens mathematisch zu rechtfertigen, da ihnen ein bestimmtes mathematisches Prinzip – die Anwendung zweier verschiedener Maßstabe für die horizontale und die vertikale Richtung – zugrunde liegt. Unbedingt verwerflich aber sind die Reliefgloben, da ihnen ein mathematisch unmögliches Prinzip – die Anwendung zweier verschiedener Maßstabe innerhalb derselben, der radialen Richtung – zugrunde liegt. Der Maßstab für den Erddurchmesser ist ungeheuer viel kleiner als der für Erhebung eines Gebirges und ändert sich plötzlich im Niveau der Meeresoberfläche. Wenn man eine derartige, nicht streng genug zu verurteilende Mißbildung betrachtet, kommt man zu der Ueberzeugung, daß die Alpen von der Nordsee aus sehr bequem sichtbar sein müssen.

F. Meisel.

Fig. 1.

Fig. 2.