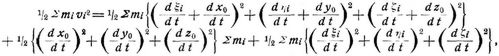Online-Bibliothek

Lebendige Kraft

[81] Lebendige Kraft (kinetische Energie, Energie der Bewegung) eines Massenpunktes ist das halbe Produkt ¹/₂ m v² aus dessen Masse m und dem Quadrat seiner Geschwindigkeit v. Bei einem Massensystem ist die lebendige Kraft ¹/₂ Σ m_i v_i² die Summe der lebendigen Kräfte sämtlicher Massenpunkte. Die lebendige Kraft ist weder dem Begriff noch der Dimension nach eine Kraft, sie ist auch keine gerichtete Größe, sondern eine stets positive Zahlengröße. Sie lieht in nächster Beziehung zur Arbeit der Kraft, als deren Aequivalent sie erscheint (s. Arbeit).

Bei der freien Bewegung eines Massenpunktes unter dem Einflusse einer Kraft P mit den Komponenten X, Y, Z gilt (s. Prinzip der lebendigen Kraft) X d x + Y d y + Z d z = d (¹/₂ m v²) = P cos α d s, wo d s das zurückgelegte Wegelement, α den Winkel zwischen seiner Richtung und jener der Kraft bedeutet. Ist die Kraft von einer Kräftefunktion U der Koordinaten ableitbar, also d U = X d x + Y d y + Z d z, so geht aus der vorigen Gleichung durch Integration über einen endlichen Weg:

hervor. Diese Gleichung sagt aus, daß die Differenz der lebendigen Kraft eines Massenpunktes an zwei Stellen seiner Bahn gleich ist der Differenz der Kräftefunktion an diesen Stellen und gleich der Arbeit der wirkenden Kraft auf dem durchlaufenen Wege. Die Gleichung gilt auch dann noch, wenn der Punkt auf einer glatten Fläche oder Kurve läuft, da die Arbeit des von der Fläche oder Kurve ausgeübten Druckes, der senkrecht auf der Bahn steht, Null ist. Schreibt man die vorige Gleichung in der Form: ¹/₂mv² – U = ¹/₂mv₀² – U₀ = const., so läßt sie sich auch so aussprechen: Die Summe aus der kinetischen Energie (¹/₂mv²) und der potentiellen Energie (–U) ist im Verlaufe der Bewegung konstant (Satz von der Erhaltung der Energie).

Bei einem Massensystem, das äußeren und inneren Kräften, die von einer Kräftefunktion ableitbar sind, unterworfen ist und zwischen dessen Teilen beliebige (reibungslose, von der Zeit unabhängige) Verbindungen bestehen, gibt es dieselben Beziehungen. Während jeder natürlichen Bewegung eines solchen Systems ist die Differenz der lebendigen Kräfte in zwei Lagen gleich der Differenz der Kräftefunktion in diesen Lagen und gleich der Arbeit, die die Kräfte beim Uebergang zwischen den beiden Lagen leisten, wobei die Arbeit der Verbindungskräfte, weil[81] verschwindend, außer Betracht bleibt. Auch gilt das Prinzip der Erhaltung der Energie, wonach die Summe aus der lebendigen Kraft (kinetische Energie) und der potentiellen Energie (gleich der negativen Kräftefunktion) im Laufe der Bewegung konstant bleibt. Systeme der genannten Art heißen konservativ; sie behalten ihren Energieinhalt bei und es ist ihre lebendige Kraft (ähnlich wie bei einem einzelnen Massenpunkt) bei gleicher Lage stets gleich, auf welchem Wege auch diese Lage wieder erreicht sein mag. Den Gegensatz hierzu bilden dissipative Systeme, welche infolge von Reibung oder andern Widerständen, die keiner Kräftefunktion genügen, dauernd Energie verlieren.

Die lebendige Kraft eines Massensystems läßt sich mit Hilfe des Massenmittelpunktes (Schwerpunktes) (x₀, y₀, z₀) umformen. Sind x_i y_i z_i die Koordinaten von m_i auf das ursprüngliche System, ξ_i, η_i ζ_i auf ein paralleles durch den Schwerpunkt gehendes System bezogen, so wird

da die Summe der doppelten Produkte wegen Σ m_i ξ_i = Σ m_i η_i = Σ m_i ζ_i = 0 verschwindet. Es ist also die lebendige Kraft eines Massensystems gleich der Summe der lebendigen Kraft der im Schwerpunkt vereinigten Gesamtmasse und der lebendigen Kraft der Bewegung um den Schwerpunkt. Die lebendige Kraft eines um eine Achse sich drehenden starren Systems ist ¹/₂ w² Σ m_i r_i² = ¹/₂ w² M k², wo w die Winkelgeschwindigkeit, – Σ m_i r_i² das Trägheitsmoment um die Achse, k den zugehörigen Trägheitsradius und M die Gesamtmasse bedeutet. Die lebendige Kraft eines beliebigen starren Systems ist ¹/₂M(v₀² + w²k²). Hierbei ist v₀ die Geschwindigkeit des Schwerpunktes, k der Trägheitsradius für die durch den Schwerpunkt gezogene Parallele zur Drehachse.

Der Satz vom Zusammenhang der lebendigen Kraft und der Arbeit reicht hin, um die Bewegung eines Systems von einem Freiheitsgrad, z.B. einer Maschine, zu bestimmen, sobald die treibenden und die widerstehenden Kräfte bekannt sind und die Bewegung zu einem bestimmten Zeitpunkt gegeben ist. Bei einem solchen System bestimmt nämlich die lebendige Kraft eindeutig die Bewegung. Um also die Bewegung zu einem späteren Zeitpunkt zu finden, braucht man nur zur lebendigen Kraft der Ausgangszeit die Differenz der Arbeit der treibenden und widerstehenden Kräfte hinzuzufügen und aus der so erhaltenen lebendigen Kraft des späteren Zeitpunktes die Bewegung zu berechnen.

Literatur: Helmholtz, Ueber die Erhaltung der Kraft, Wissensch. Abh., S. 12, und Ostwalds Klassiker, Nr. 1; Jacobi, Vorlesungen über Dynamik, herausg. von Clebsch, Berlin 1866, 4. Vorlesung, S. 18 ff.; Apell, Traité de mécanique rationelle, Paris 1893–96, Bd. 2, S. 92–126; Thomson u. Tait, Handbuch der theoretischen Physik, Braunschweig 1871, S. 229; Schell, Theorie der Bewegung und der Kräfte, 2. Aufl., Leipzig 1879, Bd. 1, S. 355 ff., und Bd. 2, S. 529–544; ferner gehört hierher die im Art. Energie angeführte Literatur.

(Schell) Finsterwalder.