Pumpenventilhub
[293] Pumpenventilhub ist in seinem Verlauf maßgebend für die Geschwindigkeit, mit der eine Pumpe arbeiten darf, ohne zu schlagen.
Die Erhebung beginnt durch den Eröffnungsstoß, den v. Bach mittels eines Indikators mit gespannt gehaltener Feder gemessen hat [3]. Der plötzliche Ueberdruck erteilt dem Ventil eine Anfangsgeschwindigkeit, die gleich der augenblicklichen Strömung des Wassers im Ventil ist, um so höher, je größere Geschwindigkeit der Kolben nach Ueberschreitung des Totpunktes schon angenommen hat. Die Verspätung, gemessen durch den Kurbelwinkel δ (s. Pumpenventilgleichgewicht, Fig. 4) ist bedingt durch den verspäteten Abschluß des mitarbeitenden Ventils und noch etwas größer, wenn der Pumpenzylinder elastisch nachgibt oder Luft enthält, schon wenn er mit dem federnden Indikator in Verbindung steht [6].
Die Berechnung des Ventilspieles sei für eine Pumpe mit Kurbelantrieb ohne Rücksicht auf den Einfluß der Pleuelstange durchgeführt, alle Maße in Metern. Die Kolbenfläche F, der Hub 2 R und die Drehgeschwindigkeit ω = 2 π n/60 = 0,1 n fördert sekundlich Q = F R ω/π und bewirkt bei der Kolbengeschwindigkeit R ω sin α im Ventilsitz f die Strömung c mit dem Höchstwert cm = F R ω/f, dem Durchschnittswert 2 cm/π und jeweilig c = cm sin α. Das Ventil beginnt mit v0 = cm sin δ und steigt mit der Geschwindigkeit v, die nach Hubmitte negativ wird, bis es mit vs = – cm sin δ im Winkel δ jenseits des Totpunktes wieder auf den Sitz trifft. Die Verspätung ergibt sich daraus, daß das Ventil selbst (wie ein beweglicher Kolben) das Wasser verdrängt und – bei stillstehendem Pumpenkolben – die Menge s v durch den Spalt hindurchlassen muß. Dabei fließt aber im Spalt das Wasser niemals zurück, sondern wegen der Ventilbelastung immer von unten nach oben durch, mit der Geschwindigkeit c1. Es ist in jedem Augenblick f c – f v = h u c1. Unter der Annahme, daß c1 konstant ist, läßt sich mit v = d h/d t die Gleichung integrieren, und man erhält, in Uebereinstimmung mit der Theorie von Westphal [4] und der Rechnung von Müller [1], für das Ventil eine Sinusbewegung mit h = hm sin (α – δ), v = v0 cos (α – δ) und der Beschleunigung d v/d t = – h ω2, Die Beschleunigung bedingt einen geringen Unterschied zwischen der Belastung und dem Wasserüberdruck, der sich jeweils dementsprechend einstellt.
Setzt man dem Pumpenventilgleichgewicht gemäß c1 = μ P √(2 g P/f γ) veränderlich ein, so darf man für v den vorigen Verlauf beibehalten, ähnlich wie Berg [6] mit einer kleinen Abweichung rechnet. Man erhält mit x = h u /f die Bewegungsgleichung cm cos δ sin (α – δ) = c1 x. Nach Fig. 3 im Art. Pumpenventilgleichgewicht sei näherungsweise μ P2 = 1/(1 + 5 x) für das Tellerventil und μ P2 = √(0,5 + 4 x) für das Kegelventil angenommen, ferner P = P0 (1 + k x) gesetzt und c0 = √(2 g P0/f γ). P0 ist die Belastung des Ventils in der Schlußstellung und besteht aus dem Gewicht des Ventils in der Flüssigkeit und dem Druck der Feder bei der Länge l0 (Fig. 5 auf S. 292). Bei der Erhebung auf h Meter wächst der Federdruck um 100 C h, wenn C in Kilogramm/Zentimetern die Federkonstante angibt; (nach Bd. 3, S. 659 ist mit den dortigen Bezeichnungen in Zentimetern C = P/f, z. B. für die zylindrische Schraubenfeder von rundem Messingdraht mit E = 1000000 ist C = 6000 d4/n r3). Dagegen vermindert sich die wirksame Ventilbelastung mit der Erhebung wegen des Beschleunigungsdruckes – m h ω2, wobei in Rücksicht auf das mit dem Ventil zu verzögernde Wasser die Masse m = P0/g statt G/g gerechnet werden mag. Hiernach wird P = P0 + 100 C h – P0 h ω2/g, folglich k = (f/u) [100 C/P0 – (n/30)2]. Für das Beispiel in [5] ist C = 50 und k = 0,25. Wenn ein Tellerventil den Wert k = 5 hätte und der Verlauf eine Sinusbewegung in der Bewegungsgleichung, wäre
Statt dessen ergibt sich für k = 0 eine in der Mitte überhöhte Linie (Fig. 4 auf S. 292). In vorstehender Figur ist der wirkliche Verlauf im Vergleich mit der gestrichelten Sinuslinie aufgezeichnet [3], [5], [6]. Sobald das Ventil von der Linie der Gleichgewichtslagen abweicht, treten starke Druckdifferenzen, besonders infolge der veränderten Strömung auf, die es pendelnd der normalen Lage zuführen. Felle Hubbegrenzungen sind dabei unnötig und Hörend [3].
Die größte Erhebung hm bezw. xm findet sich, indem man in der Bewegungsgleichung cos δ und sin (α – δ) = 1 setzt. Für k = 5 wird xm = cm/c0; für ein Gewichtsventil mit k = 0 ist
für
[293] Für den Verspätungswinkel erhält man, indem man die Bewegungsgleichung nach der Zeit differentiiert, tg δ = f α/u c0, und zwar nach [4] 2–6°.
Aus Versuchen mit gewichtsbelasteten Pumpenventilen folgert v. Bach [3], daß die Grenze des Ventilschlages proportional F R ω2/P0 ist, und Berg gibt für mäßige Federbelastung an [6], daß die Höhenlage des Ventils am Totpunkt bei α = π, nämlich xπ = (cm/c0) cos δ sin δ oder (cm/c0) tg δ = 0,016 werden darf, also u c02 > 20 Q n. Westphal [4] stellt auf Grund von Betriebserfahrungen als Bedingung für schlagfreien Ventilschluß auf, daß die Schlußgeschwindigkeit nicht größer als 0,1 m/sec sein soll, woraus folgt u c0  π Q n oder hm
π Q n oder hm 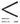 1/n.
1/n.
Eine Ausnahme von der Theorie macht das im Pumpenventilgehäuse (S. 292) gezeichnete, noch nicht ausgeführte Ventil, weil es sich bereits im Totpunkt auf seine Tragfläche in der Mitte aufsetzen kann, während die Lederliderung am Spalt das vom Kolben zuletzt noch angesaugte oder verdrängte Wasser eben noch durchläßt. Fernisventile und biegsame Gummiklappen kommen ihm darin nahe.
Literatur s. Pumpenventile.
Lindner.
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum
