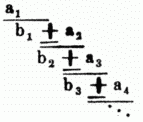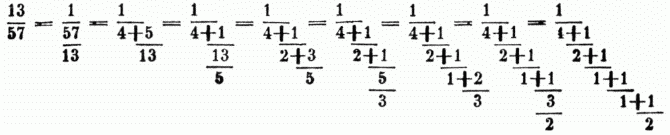Kettenbruch

[448] Kettenbruch (Continuirlicher Bruch), Bruch, dessen Nenner eine gemischte Zahl ist, deren Bruch selbst wieder zum Nenner eine eben solche gemischte Zahl hat etc., entweder bis zu einem bestimmten Ende (endlicher K.) od. ohne Ende (unendlicher K.). Unter gewöhnlichen od. gemeinen Kettenbrüchen versteht man solche, wo alle Zähler des zweiten Gliedes einer jeden solchen gemischten Zahl nicht nur unter einander gleich, sondern auch gleich 1 sind. Ein K. überhaupt hat also z.B. diese Form:

ein gemeiner, mit denen wir uns beschäftigen, würde sein

Die einzelnen Brüche, wie 1/b₁, 1/b₂ etc., heißen die Glieder des K-s. Die Nenner pflegt man wohl auch rücksichtlich ihrer Entstehungsweise Quotienten zu nennen. Wenn die Glieder eines unendlichen K-s von irgend einem Gliede an stets in derselben Ordnung u. mit demselben Vorzeichen wiederkehren, so heißt er ein periodischer. Die Werthe, welche man erhält, wenn man beim ersten, zweiten, ..ten Nenner abbricht, heißen resp. der erste, zweite, ..nte Nährungsbruch. Man kann jeden gemeinen Bruch in einen K. verwandeln mit Anwendung des Satzes, daß, wenn man vom reciproken Werthe einer Größe wieder den reciproken Werth nimmt, man die Größe selbst erhält; z.B. ¹³/₅₇ soll in einen K. verwandelt werden:

Hieraus ergibt sich die Regel: Man dividirt mit dem kleineren Theile des gegebenen Bruchs in den größeren, mit dem dabei erhaltenen Rest in den vorigen Divisor u. fährt so fort, bis der letzte Divisor = 1 ist, was immer sein muß, wenn man den gegebenen Bruch zuvor durch die kleinsten Zahlen ausdrückt, u. nimmt die hierbei gefundenen Quotienten zu den auf einander folgenden Nennern des K-s. Eben so kann man jeden einfachen K. in einen gemeinen Bruch verwandeln, indem man Schritt für Schritt die vorher angegebene Weise rückwärts ausführt. Bei der Ausziehung der Quadratwurzeln u. Auflösung quadratischer Gleichungen u. unbestimmter Gleichungen leisten die Kettenbrüche gute Dienste. Erst im Anfang des 17. Jahrh. findet man Spuren von den Kettenbrüchen, indem Brounker (1620–84) ein Verhältniß des Quadrats des Durchmessers zum Inhalt des Kreises durch einen K. bestimmte. Huygens (1629–95) zeigte, wie Kettenbrüche dazu dienen, das Verhältniß [448] zweier großen Zahlen durch kleinere beinahe auszudrücken, so daß keine kleineren es genauer angeben. Euler (1707–83) stellte eine vollständige Theorie derselben auf u. auch transscendente Formen durch sie dar. Vgl. Kausler, Lehre von den continuirlichen Brüchen, Stuttg. 1803; Stern, Theorie der Kettenbrüche, Berl. 1834.