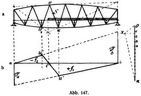
Frei aufliegende Balken
[205] Frei aufliegende Balken (Träger). Alle mit voller oder durchbrochener Wandung (Vollwand-, Gitter- oder Fachwerksträger) ausgeführten Träger, die auf zwei festen Stützen derart gelagert sind, daß zum mindesten der Druck auf eine der beiden Stützen stets lotrecht gerichtet ist. Hiezu ist erforderlich, daß ein Lager wagrecht verschiebbar ist. In allgemeinerer Auffassung müßten auch jene Träger hierher gezählt werden, bei denen ein Stützendruck eine unveränderliche, durch die Neigung des Gleitlagers bestimmte Richtung hat (schief gelagerter Balkenträger). Für lotrecht wirkende Belastungen, mit denen man es der Hauptsache nach immer zu tun hat, sind demnach bei wagrechter Auflagerung auch beide Stützendrücke lotrecht.
I. Die äußeren Kräfte.
Führt man in der Entfernung x vom linken Auflager A (Abb. 128) einen Schnitt durch den Träger senkrecht zu dessen Längsachse, so müssen die in diesem Querschnitt auftretenden Spannungen den äußeren Kräften, die auf den abgetrennten Trägerteil wirken, das Gleichgewicht halten. Diese äußeren Kräfte lassen sich durch eine in der Querschnittsebene wirkende lotrechte Kraft (Querkraft, Transversalkraft) Q und durch ihr drehendes Moment (Angriffs- oder Biegungsmoment) M ersetzen. Die Querkraft wird positiv genommen, wenn sie auf den linken Trägerteil nach aufwärts wirkt, und das Moment, wenn es die beiden Trägerteile nach oben gegen einander zu drehen, also den Träger nach oben konkav ( ) zu biegen sucht. Es handelt sich zunächst um Bestimmung dieser Größen, wobei mit Rücksicht auf die zufällige (Verkehrs-) Belastung die ungünstigsten Einwirkungen in Betracht zu ziehen sind.
) zu biegen sucht. Es handelt sich zunächst um Bestimmung dieser Größen, wobei mit Rücksicht auf die zufällige (Verkehrs-) Belastung die ungünstigsten Einwirkungen in Betracht zu ziehen sind.
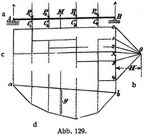
a) Ruhende oder bleibende Belastung. Besteht diese aus einer Reihe von Einzellasten, die in bestimmten Abständen von den Stützen angreifen (Abb. 129) und bezeichnet man die Strecken BP1 mit ξ1, BP2 mit ξ2 ....., so berechnen sich die Stützendrücke aus
1)
und es werden die Querkräfte für alle Querschnitte
| in der Strecke AC1 | Q1 = A |
| in der Strecke C1C2 | Q2 = A – P1 |
| in der Strecke G2C3 | Q3 = A – P1 – P2 |
u.s.w. Das Angriffsmoment im Punkt M
wird
M = Ax – P1 (x + ξ1 – l) – P2 (x + ξ2 – l) 2)
[205] wenn die Stützweite A B mit l bezeichnet wird.
Das zeichnerische Verfahren zur Bestimmung der Querkräfte und Momente beruht auf der Konstruktion eines Seilecks zwischen den Kräften P (Abb. 129 a–d). Es werden diese Kräfte nach einem angenommenen Maßstab als Strecken dargestellt und in dem Kräftepolygon (Abb. 129 b) aneinander gereiht. Die von dem beliebig, in der Polweite H, gewählten Pol O zu den Enden der Kraftstrecken gezogenen Strahlen bestimmen die Richtungen der Seiten des Seilecks (Abb. 129 d). Die Schlußseite dieses letzteren, die die mit den Lotrechten durch die Auflager erhaltenen Schnittpunkte a b verbindet, gibt die Richtung des Polstrahls O X, durch den die beiden Auflagerdrücke bestimmt werden. Dadurch sind auch die Querkräfte gegeben (Abb. 129 c), während die Momente durch die Höhen y des Seilecks gemessen werden. Es ist nämlich
M = H . y,
wobei H in Krafteinheiten, y in Längeneinheiten auszudrücken ist.
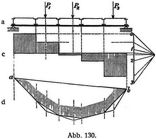
Können sich die Lasten nicht unmittelbar, sondern nur an gewissen Knotenpunkten durch Vermittlung von Quer- und Längsträgern auf den Hauptträger übertragen (Abb. 130 a), welche Anordnung der gewöhnlichen Ausführung entspricht, so zerlegt sich eine jede zwischen zwei Knotenpunkten angreifende Last in zwei daselbst wirkende Seitenkräfte und für diese wird die Momentenlinie aus dem Seileck der Kräfte P in der in Abb. 130 d dargestellten Weise erhalten. Hiernach werden die Momente in den Knotenpunkten ebenso groß wie bei unmittelbarer Belastung des Trägers.
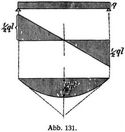
Für eine stetige Belastung (Abb. 131) geht das Seileck in eine Seilkurve über. Diese nimmt für den Fall einer gleichmäßig verteilten Belastung (q f.d. Längeneinheit) die Form einer Parabel an, und zwar wird bei gänzlicher und unmittelbarer Belastung des Trägers
3)
4)
Bei mittelbarer Belastung ist die Momentenlinie ein der Seilkurve (Parabel) eingeschriebenes Vieleck, dessen Eckpunkte auf den Senkrechten durch die Knotenpunkte liegen.
b) Verkehrsbelastung. α) Diese möge aus einem Zug von Einzellasten bestehen, die ohne Änderung ihrer gegenseitigen Abstände auf dem Träger beliebig verschoben werden können.
Um bei unmittelbarer Belastung die größte Querkraft in einem Querschnitt zu erhalten, hat man in der Regel die vorderste Last über diesen Querschnitt zu bringen und den Belastungszug, je nachdem es sich um die größte positive oder negative Querkraft handelt, entweder nach rechts oder nach links sich erstreckend so anzunehmen, daß die schwersten Lasten sich an der Spitze des Zuges befinden.
Für diesen Belastungsfall (Lasten nur auf einer Seite des Querschnittes) ist die Querkraft durch den linken, bzw. rechten Stützendruck bestimmt. Bezeichnet P1 P2 P3 ... die Lasten, e1e2 ... ihre gegenseitigen Abstände, ξ1ξ2 ... deren Abstände von der rechten Stütze, so ergibt sich
Qmax = A = 1/l Σ P ξ 5)
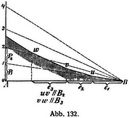
Die größten Querkräfte in den einzelnen Querschnitten sind sonach durch die Linie des Stützendruckes A bestimmt, der beim Vorschieben[206] des Lastenzugs in der linken Stütze auftritt. Diese A-Linie kann aus 5) durch Rechnung oder durch graphische Ausmittlung (nach Abb. 132) erhalten werden.
Ist P1/e1 < ΣP/l, was dann eintritt, wenn die erste Last klein ist und von der nächstfolgenden weit absteht, so wird die Querkraft nicht für die Grundstellung (erste Last am Querschnitt), sondern dann am größten, wenn die zweite Last über den Querschnitt gestellt wird. Für die gewöhnlichen Belastungszüge tritt indes dieser Fall nicht ein.
Können sich die Lasten mittels Querträgern nur in bestimmten Knotenpunkten auf den Träger A B übertragen, so bleibt die größte Querkraft zwischen je zwei Knoten gleichgroß und sie tritt in der Regel wieder dann auf, wenn die erste Last an dem rechten Querträger gelegen ist. Nur bei großer Knotenweite a und vorangehenden kleinen Lasten kann die Querkraft noch zunehmen, wenn die ersten Lasten in das Feld a eintreten. Sind G0 diese innerhalb des Felds gelegenen Lasten, ist Σ P die Summe aller auf dem Träger befindlichen Lasten, so tritt der oberwähnte Fall ein, wenn G0/a < ΣP/l ist. Die Konstruktion (Abb. 133) gibt hierüber Aufschluß. Man zeichnet zunächst die A-Linie für die unmittelbare Belastung wie in Abb. 132 und führt dieselbe Konstruktion auch für die einzelnen Feldweiten durch, um durch die Ordinaten der Linie N o' p' q' die Drücke auf den linken Querträger M infolge der in der Feldweite M N liegenden Lasten zu erhalten. Dieselben sind von den Ordinaten der Linie B Q in Abzug zu bringen und die in dem betreffenden Feld übrigbleibende größte Ordinate bestimmt daselbst die Querkraft.
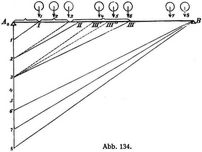
Das größte Moment bei unmittelbarer Belastung in einem Trägerquerschnitt tritt auf, wenn möglichst viele Lasten auf den Träger, und zwar die schwersten in die Nähe des betreffenden Querschnittes, gebracht werden und wenn dabei gleichzeitig eine Last über den Querschnitt selbst gestellt wird. Bei einem gegebenen Lastenzug handelt es sich sonach zunächst um die Ermittlung jener maßgebenden Last, durch deren Stellung über den betrachteten Querschnitt das größte Moment hervorgerufen wird. Es ergibt sich, daß die ganze Trägerlänge in Abschnitte zerfällt, in denen der Reihe nach die 1., 2., 3. u.s.w. Last als maßgebend erscheint. Diese Abschnitte verhalten sich, solange nicht neue Lasten auf den Träger treten, zueinander wie die Lastgrößen, und es kann daher zu ihrer Ermittlung die vorstehende Konstruktion (Abb. 134) benutzt werden. Auf der Senkrechten durch A trage man die Lastgrößen als Strecken 01, 12, 23 ... auf, ziehe durch das Ende der letzten Last, die auf dem Träger noch Platz findet, die Linie nach B und hierzu Parallele durch die einzelnen Teilpunkte der Laststrecken. Hierdurch werden auf dem Träger A B die Abschnitte A I, I II u.s.w. erhalten, in denen die 1., bzw. 2 ... Last zur Hervorbringung des größten Moments über den Querschnitt zu stellen ist. Fallen bei der Verschiebung des Lastenzugs einzelne Lasten über den Träger hinaus, so ist darauf entsprechend Rücksicht zu nehmen. Aus diesem Grund wurde beispielsweise in Abb. 134 der Punkt III so bestimmt, daß durch 3 die Parallele zu B6 gezogen wurde, da bei Stellung der Last 3 in III', bzw. III''' die Lasten 8, bzw. 7 bereits über den Träger weggerückt sind.
Ist P die am Querschnitt liegende Last, gibt man ferner den links davon gelegenen Lasten und ihren Abständen von der Stütze A den Index l, den rechts gelegenen Lasten und deren Abständen von B den Index r, so drückt sich das Moment in M aus durch
6)
[207] Werden die Abstände der Lasten von der am Querschnitt liegenden Last P eingeführt und mit e bezeichnet, ist ferner Σ P die Summe aller Lasten, so läßt sich der Ausdruck für das Moment auch in der Form schreiben
7)
und hiernach wird auch die Berechnung ziemlich vereinfacht, indem man die Momentensummen Σ P e tabellarisch aufstellen oder sich eines sogenannten Momentenschemas bedienen kann.
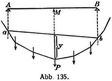
Die graphische Ermittelung der größten Momente beruht auf der Zeichnung des Seilecks für das gegebene Lastensystem. Hat man nach dem früheren (Abb. 134) für den Querschnitt M die maßgebende Last P bestimmt, so ist die Schlußlinie a b im Seileck (Abb. 135) so einzutragen, daß die Horizontalabstände der der Last P entsprechenden Ecke von a und b den Abständen des Querschnitts M von den Stützen A und B entsprechen. Die unter M gemessene Ordinate y mit H multipliziert gibt das Maximalmoment.
Trägt man die Werte der Maximalmomente für die einzelnen Querschnitte als Ordinaten auf, so erhält man, wie sich aus dem Ausdruck 7) folgern läßt, eine aus Parabelstücken zusammengesetzte Kurve. Das absolut größte Moment tritt nahe der Mitte des Trägers auf, nämlich in einem Querschnitt, der mit der Resultierenden sämtlicher Lasten symmetrisch zur Trägermitte gelegen ist. Da man nach dem Vorhergehenden die maßgebende Last für die mittlere Trägerstrecke kennt, so läßt sich hiernach auch der Querschnitt, in dem das absolut größte Moment eintritt und dieses selbst von vornherein angeben.
Nach der österreichischen Brückenverordnung kann für die Belastungszüge der Haupt- und Nebenbahnbrücken der einer Stützweite zugehörige Größtwert des Moments den der Verordnung beigegebenen Tabellen entnommen werden. Mit dieser Maximalordinate kann man annähernd die Linie der Maximalmomente verzeichnen, aus zwei Parabelästen bestehend, deren Scheitel um 0∙1 l abstehen und durch eine horizontale Gerade verbunden sind.
Bei mittelbarer Belastung des Hauptträgers genügt es wieder, die Momente nur für jene Stellen zu bestimmen, an denen die Querträger aufliegen, und für die dazwischen liegenden Querschnitte die Momentenlinie gerade anzunehmen.
β) Wird die Verkehrsbelastung als stetige gleichmäßig verteilte Last p f.d. Längeneinheit angenommen, so ergibt sich bei unmittelbarer Belastung die größte Querkraft, wenn die Belastung vom Querschnitt M bis zur rechten Stütze reicht. Der analytische Ausdruck hierfür lautet, wenn x der Abstand des Querschnittes von der linken Stütze:
8)
Die größte negative Querkraft, die bei Belastung des linksseitigen Trägerteils A M entsteht, wird
9)
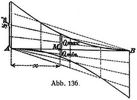
Die graphische Darstellung (Abb. 136) gibt eine Parabel, deren Scheitel in B, bzw. in A gelegen ist.
Die Momente werden bei gänzlicher Belastung am größten, und stellen sich durch die Ordinaten einer Parabel dar, deren Scheitelhöhe in der Trägermitte gleich 1/8 p l2 ist. Für den beliebigen Querschnitt M wird
10)
Kann sich die Belastung nur in einzelnen Punkten auf den Hauptträger absetzen, so entsteht die größte Querkraft in einem Fach, wenn die Belastung noch einen Teil der Feldweite a überdeckt. Ist x' der Abstand des rechten Querträgers von der Stütze B, so ist über diesen Querträger hinaus noch eine Strecke
zu belasten; die größte Querkraft im betreffenden Fach wird
11)
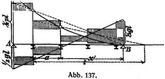
[208] Die Konstruktion ist nach Abb. 137 durchzuführen.
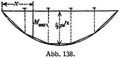
Für die Maximalmomente ergibt sich ein der Parabel in Abb. 138 eingeschriebenes Polygon, dessen Ecken auf den Senkrechten durch die Knotenpunkte liegen.
II. Die inneren Kräfte.
A. Vollwandige Träger. Die Normalspannungen in einem auf Biegung beanspruchten vollwandigen Balken berechnen sich aus
σ = M v/J 12)
wenn J das Trägheitsmoment des Querschnitts, v den parallel zur Kraftebene gemessenen Abstand der Fasern von der betreffenden Schwerpunktsachse und M das Biegungsmoment bezeichnet. Die größten Normalspannungen σmax treten hiernach in den äußersten Fasern auf.
Die Schubspannung in einer Faserschicht von der Breite b parallel zur Schwerpunktsachse wird
τ = Q S/J b 13)
Hierin ist Q die Querkraft, S das statische Moment des über der Faserschicht gelegenen Querschnittsflächenteils.
B. Fachwerksträger. Ein Fachwerk besteht aus stabförmigen, an ihren Enden gelenkartig verbundenen Gliedern. Für die praktische Anwendung zu Trägern kommen nur solche Anordnungen in Betracht, bei denen sämtliche Stabglieder in einer Ebene liegen und bei gleichbleibender Temperatur nur elastische, d.i. von dem Auftreten von Spannungen begleitete Verschiebungen annehmen können. Solche Fachwerke werden als starr oder stabil bezeichnet, im Gegensatz zu den schlaffen oder beweglichen Stabsystemen, bei denen auch ohne Längenänderung der Stäbe kleine oder unbeschränkt große Verschiebungen vor sich gehen können und die für sich allein als Träger nicht brauchbar sind. Die Starrheit oder geometrische Bestimmtheit eines Fachwerks wird durch entsprechende Anzahl und Gruppierung der das Fachwerk zusammensetzenden Stäbe erreicht. Sind z.B. k Knotenpunkte (Vereinigungspunkte der Stäbe) vorhanden, so ist zur Starrheit des Fachwerks erforderlich, daß die Anzahl der die Knotenpunkte verbindenden und in ihren Längen voneinander unabhängigen Stäbe 2 k – 3 beträgt. Ein mit dieser geringsten Anzahl von Stäben konstruiertes starres Fachwerk ist gleichzeitig auch statisch bestimmt, d.h. zur Ermittelung der in den Stabgliedern auftretenden Spannungen genügen die Sätze über das Gleichgewicht und die Zerlegung von Kräften in der Ebene, ohne daß auf die elastischen Formänderungen eingegangen zu werden braucht. Ist dagegen die Zahl der Stäbe eines Fachwerks oder von einem k Knotenpunkte enthaltenden Teile größer als 2 k – 3, so bezeichnet man das Fachwerk als überstarr. Ein solches ist statisch unbestimmt, da zur Ermittelung der darin auftretenden Spannungen die statischen Gleichgewichtsbedingungen nicht mehr ausreichen und auf die elastischen Formänderungen eingegangen werden muß.
Statisch bestimmte, stabile Fachwerke werden im allgemeinen erhalten, wenn an eine starre Grundfigur (Einzelstab, Stabdreieck u.s.w.) weitere Knotenpunkte durch je zwei Stäbe angeschlossen werden. Hierdurch kommen einfache Dreieckssysteme zu stande, wofür die Abb. 139 u. 140 Beispiele zeigen. Dagegen gehören die mehrteiligen Fachwerke (Abb. 141, 142 u. 143) zu den statisch unbestimmten Systemen. Über die verschiedenen Formen der Fachwerksträger s. »Eiserne Brücken«. Zur Berechnung der Stabkräfte eines Fachwerks stehen uns zwei Methoden zur Verfügung. Jede kann entweder zu analytischen oder graphischen Berechnungsverfahren verwertet werden.
1. Die Knotenpunktsmethode geht vom Gleichgewichte der an den Knoten angreifenden Kräfte aus. Für die analytische Behandlung ergeben sich hieraus bei k Knotenpunkten 2 k Bedingungsgleichungen, von denen aber drei nicht unabhängig sind, sondern zufolge des Gleichgewichts der äußeren Kräfte erfüllt sein müssen. Es können sonach 2 k – 3 Stabkräfte berechnet werden. Graphisch führt diese Methode zum Cremona-Plane, der dadurch erhalten wird, daß man die an jedem Knoten wirkenden Kräfte zu einem Krafteck zusammensetzt, das[209] sich dann verzeichnen läßt, wenn an einem Knotenpunkte nur je zwei unbekannte Stabkräfte vorkommen. Die Methode des Cremona-Planes ist zweckmäßig anzuwenden, wenn für einen und denselben Belastungszustand sämtliche Stabkräfte zu bestimmen sind, wie dies bei den Spannungen infolge des Eigengewichtes der Fall ist.
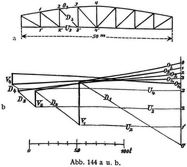
In Abb. 144 b ist der Kräfteplan für den Träger nach Abb. 144 a dargestellt, u.zw. ist am Untergurt eine vollständige Belastung von 3 t f.d. Längenmeter, am Obergurt eine solche von 0∙8 t angenommen und wurden die hierfür bestimmten Knotenlasten in den Strecken 0 1, 1 2, 2 3 .. 0'1, 1'2', 2'3' .... aufgetragen. Die Regel, die bei der Zeichnung des Kräfteplans zu beobachten ist, lautet: Man ziehe durch die Teilpunkte der Knotenlasten Parallele zu den betreffenden Gurtungen und zwischen diesen Parallelen einen Linienzug parallel zu den Füllungsgliedern.
2. Schnittmethode. Denkt man sich durch das Fachwerk einen Schnitt so geführt, daß drei nicht von demselben Knotenpunkt ausgehende Stäbe getroffen werden, so lassen sich die Spannungen dieser Stäbe mit Rücksicht auf die Bedingung bestimmen, daß sie den auf den abgetrennten Trägerteil wirkenden äußeren Kräften das Gleichgewicht halten müssen. Die Ermittlung der Stabkräfte kann wieder entweder rechnerisch oder graphisch erfolgen. Es ist dieses Verfahren dem unter 1) insbesondere dann vorzuziehen, wenn es sich für einen bestimmten Belastungszustand nur um einzelne Stabkräfte handelt und für die verschiedenen Stäbe verschiedene Belastungszustände in Frage kommen (Verkehrslast).
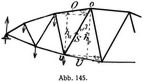
Mit Einführung der aus der Abb. 145 ersichtlichen Bezeichnung erhält man für die Gurtkräfte
14)
für die Kraft in dem die Knotenpunkte O U verbindenden Ausfachungsstabe
15)
oder
16)
Es bezeichnet darin M0 und Mu das Moment der auf den abgetrennten Trägerteil wirkenden äußeren Kräfte bezogen auf die den betreffenden Gurtstäben gegenüber oder dem Wandstab anliegenden Knotenpunkte und Q die lotrechte Querkraft in dem geführten Schnitte.
Für den Parallelträger (Träger mit geraden, parallelen Gurten) ist
Das negative Vorzeichen bedeutet eine Druck-, das positive eine Zugspannung. Für den einfachen, frei aufliegenden Träger nehmen die Momente nur positive Werte an, der Obergurt wird demnach durchaus gedrückt, der Untergurt gezogen. Das negative Vorzeichen der Strebenkraft gilt für gegen die Trägermitte steigende Streben. Diese werden sonach im allgemeinen gedrückt, die fallenden Streben werden gezogen.
Die Gurtkräfte werden für jene Belastung am größten, die die größten Momente in den Knotenpunkten hervorruft; ihre Berechnung erfolgt am einfachsten nach den obigen Formeln aus den Knotenpunktsmomenten, deren Größtwerte graphisch oder durch Rechnung bestimmt werden können. Beim Parallelträger sind ebenso auch die größten Stabkräfte in der Ausfachung durch die Größtwerte der Querkräfte gegeben.
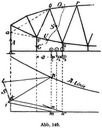
Beim krummgurtigen Fachwerksträger sind dagegen die Wandstabkräfte nicht in so einfacher Weise bestimmt und es ist die ungünstigste Belastungsweise in der Fachweite des Wandstabes im allgemeinen nicht mit jener für die größte Querkraft übereinstimmend. Sieht man jedoch davon ab und nimmt man als ungünstigste Verkehrsbelastung für einen Wandstab jene an, die die größte Querkraft im betreffenden Fache hervorruft, so läßt sich die Stabkraft wieder entweder durch Rechnung nach Formel[210] 15) oder 16) oder auf graphischem Wege ermitteln. Letzterer ist aus Abb. 146 zu entnehmen. Man verzeichne (nach Abb. 132) für den gegebenen Belastungszug die Linie des Stützendruckes (A-Linie) und ebenso die Linie u' n des Druckes G' auf den linken Querträger des Faches u v. Die größte Ordinate n p zwischen beiden Linien gibt die größte Querkraft im Fache, u.zw. ist  = A und
= A und 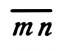 = G'. Denkt man sich G' nach Richtung von o v und u v zerlegt, letztere Komponente mit der Untergurtkraft U vereinigt und mit dem Auflagerdruck A zu einer Resultierenden zusammengesetzt, so muß diese die Richtung a o annehmen; wir erhalten sie daher durch das Kräftedreieck p m i, in dem p i || a o und m i || u v ist. Zieht man ferner k i || o v und n k || u v, so gibt
= G'. Denkt man sich G' nach Richtung von o v und u v zerlegt, letztere Komponente mit der Untergurtkraft U vereinigt und mit dem Auflagerdruck A zu einer Resultierenden zusammengesetzt, so muß diese die Richtung a o annehmen; wir erhalten sie daher durch das Kräftedreieck p m i, in dem p i || a o und m i || u v ist. Zieht man ferner k i || o v und n k || u v, so gibt  die in Richtung v o wirkende Komponente von G'. Das Gleichgewicht der Kräfte im Knotenpunkte O liefert schließlich mit p l || o r und k l || o u das Krafteck p l k i, in dem
die in Richtung v o wirkende Komponente von G'. Das Gleichgewicht der Kräfte im Knotenpunkte O liefert schließlich mit p l || o r und k l || o u das Krafteck p l k i, in dem 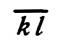 die gesuchte Stabkraft S gibt.
die gesuchte Stabkraft S gibt.
3. Methode der Einflußlinien. Bei allgemeiner Trägerform wird es für die Berechnung der von der Verkehrslast hervorgerufenen Wandstabkräfte empfehlenswerter sein, die Methode der Einflußlinien anzuwenden. Eine Einflußlinie wird erhalten, wenn man die statische Einwirkung einer über den Träger wandernden Einzellast auf einen bestimmten Konstruktionsteil des Trägers als Ordinate am jeweiligen Lastorte aufträgt. Zur Verzeichnung der Einflußlinie einer Stabkraft eines freiaufliegenden Trägers bedarf es bloß zweier Einflußgrößen für je eine rechts und links vom betreffenden Fache liegende Einzellast. Wir benutzen hierzu die Stabkräfte 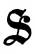 a und
a und 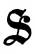 b, die durch je eine im linken und rechten Auflager wirkende lotrechte Kraft 1 bei Festhaltung des anderen Trägerendes im Stabe hervorgerufen werden. Man erhält sie für sämtliche Stäbe mittels zweier Cremona-Pläne oder durch Rechnung. In Abb. 147 stellt a u'1 u' b die Einflußlinie der Stabkraft S für Belastung der unteren Knotenpunkte dar.
b, die durch je eine im linken und rechten Auflager wirkende lotrechte Kraft 1 bei Festhaltung des anderen Trägerendes im Stabe hervorgerufen werden. Man erhält sie für sämtliche Stäbe mittels zweier Cremona-Pläne oder durch Rechnung. In Abb. 147 stellt a u'1 u' b die Einflußlinie der Stabkraft S für Belastung der unteren Knotenpunkte dar.
Mit Hilfe der Einflußlinie läßt sich die Spannung in dem betreffenden Stab sowohl infolge einer gleichmäßig verteilten Belastung, als auch infolge eines Lastenzugs angeben. Im ersteren Fall ist die der belasteten Strecke entsprechende Fläche der Einflußlinie mit der Last f.d. Längeneinheit zu multiplizieren, im letzteren Fall sind die in den Lastvertikalen gemessenen Ordinaten mit den Lasten zu multiplizieren und zu addieren. Man erkennt, daß bei gleichmäßig verteilter Belastung für die größte Spannung im Stab o u die Belastung über die Strecke i b, für die kleinste Spannung über die Strecke i a reichen muß. Der Punkt i liegt in dem Fach, dem die betreffende Strebe angehört und kann auch durch die in Abb. 147 a angedeutete Konstruktion gefunden werden. Bezeichnet g das (am Untergurt wirkend gedachte) Eigengewicht f.d. laufenden Meter, p die zufällige Last, ferner f1 und f2 die positiven und negativen Einflußflächen für den Gitterstab u o, so erhält man die Grenzspannungen aus:
Smax = (g + p) f1 – gf2 17)
Smin = gf1 – (g + p) f2 17)
Besteht die Verkehrslast aus einem Zuge von Einzellasten, so ist zunächst die ungünstigste Einstellung des Lastenzuges zu ermitteln. Um diese beispielsweise für die Größtspannung des Stabes o u zu finden, ziehe man durch die Punkte o n der Kraftstrecke (Abb. 147 c), die die n ersten Lasten begrenzen, die auf dem Träger in der Strecke u1 b Platz finden, Senkrechte o x und n x zu u'1 u' und u' b. Der Schnittpunkt x liegt in der Horizontalen durch jene Last (hier P2), die für die ungünstigste Einstellung über den rechten Knotenpunkt u[211] zu stellen ist. Sind für diese Laststellung ŋ1 ŋ2.. die Ordinaten der Einflußlinien unter den Lasten P1 P2.., so erhält man die Stabkraft aus S = Σ P η, wozu noch die Eigengewichtsspannung g (f1 – f2) hinzutritt.
C. Bestimmte Trägerformen.
α) Parallelträger. Für diesen ist in den Gleichungen 14 und 16 σ0 = σu = 0 zu setzen, wodurch sich ergibt, daß die Gurtspannungen den auf die Knotenpunkte bezogenen Momenten, die Gitterstabspannungen den Querkräften Q proportional werden. Erstere sind sonach der Linie der größten Momente, letztere jener der größten Querkräfte (Abb. 137) unmittelbar zu entnehmen. Die Gurtspannungen werden hiernach in der Trägermitte am größten und wachsen von Fach zu Fach annähernd nach den Ordinaten einer Parabel. Von den Gitterstäben erhalten jene in den Endfachen die größten Spannungen, während im mittleren Trägerteil ein Wechsel zwischen Druck und Zug in der Ausfachung eintritt. Dieser Spannungswechsel tritt in einem Fach auf, dessen linker Knotenpunkt von der linken Stütze einen größeren Abstand als
18)
hat, wenn e die Knotenweite, g das Eigengewicht und p die zufällige Last f.d. laufenden Meter bezeichnet.
β) Parabelträger. Wird die Form eines oder beider Gurte so gewählt, daß die Knotenpunkte auf einer Parabel liegen, so ist bei der Scheitelhöhe h die Höhe im Abstand x von der Stütze
und es wird bei gänzlicher gleichmäßiger Belastung des Trägers mit g + p = q f.d. Längeneinheit
Ist sonach ein Gurt gerade, so erhält er eine konstante Spannung von der Größe
19)
Die Spannung des eckigen Gurts wird
20)
Besteht das Fachwerk aus senkrechten und geneigten Stäben, so wird für eine vollkommene gleichmäßige Belastung die Spannung der geneigten Stäbe Null, jene der lotrechten Stäbe gleich dem am geraden Gurt wirkenden Knotengewicht = qu e.
Die schrägen Ausfachungsstäbe sind demnach bei totaler gleichmäßiger Belastung spannungslos; bei rechtsseitiger Belastung werden die rechtsfallenden Stäbe auf Zug, bei linksseitiger Belastung ebenso stark auf Druck beansprucht. Diese Maximal- bzw. Minimalspannung berechnet sich für die Diagonale des m∙Faches mit der Höhe hm – 1 am linken Knotenpunkte mit
sie ist demnach in jedem Fache der Länge des Diagonalstabes proportional. Die Schrägstabkräfte nehmen hier von der Mitte des Trägers gegen die Endfache zu ab.
γ) Der Schwedlerträger, von dem preuß. geh. Oberbaurat Schwedler zum ersten Male im Jahre 1863 bei der Weserbrücke zu Corvey angewandt, besitzt eine solche Gurtform, daß in dem rechtsfallenden Streben der linken Trägerhälfte bei Rechtsbelastung Zug auftritt, dagegen bei Linksbelastung ihre Spannung gerade Null wird; dies gilt in symmetrischer Übertragung auch für die rechte Trägerhälfte. Es ist sonach für die Schrägstäbe des Ständerfachwerks die obere Grenzspannung Smax Zug (+), die untere Grenzspannung Smin = 0, wogegen beim Parallelträger in den äußeren Fächern sowohl Smax wie Smin positiv, beim Parabelträger durchwegs Smax = – Smin ist. Für gleichmäßig verteilte Verkehrslast liegen bei geradem Untergurte die Knotenpunkte des Obergurts auf zwei symmetrisch gelegenen Hyperbelästen; in der Ausführung werden die höchsten Punkte der beiden Kurvenäste durch einen wagrechten Gurt verbunden.
δ) Halbparabelträger. Unter dieser Bezeichnung versteht man Träger mit parabolisch gekrümmten Gurtungen, die sich über den Auflagern nicht vereinigen, so daß daselbst noch eine gewisse Trägerhöhe h0 vorhanden ist. Gewöhnlich wird der Gurt, an dem die Fahrbahn gelegen ist, horizontal ausgeführt. Bezeichnet man die Trägerhöhe in der Mitte mit h, so folgt jene im Abstand x vom Trägerende
Für die Berechnung der Spannungen erscheint es am zweckmäßigsten, die allgemeinen Formeln 14–16 oder die graphischen Verfahren nach Abb. 146 oder mittels Einflußlinien in Anwendung zu bringen. Im allgemeinen sei nur bemerkt, daß die Spannungen der Gurte sich im mittleren Teil des Trägers, und zwar auf eine umso größere Länge, je kleiner die Endhöhe ist, nur wenig ändern und dann in den Endfeldern rasch abnehmen. Die Spannungen in der Ausfachung nehmen von den Endfachen nach der Mitte hin rascher ab, als beim Parallelträger; dagegen erstreckt sich der Spannungswechsel in der Ausfachung im mittleren Teil des Trägers auf eine umso größere Länge, je mehr sich der Träger dem reinen Parabelträger nähert.
Melan.
Brockhaus-1911: Balken [2] · Balken · Frei von Obligo · Frisch, fromm, froh, frei · Frei von Bruch · Frei bis zur Adria · Frei Schiff
DamenConvLex-1834: Frei, Frey, Freir (Mythologie)
Lueger-1904: Balken, kontinuierliche · Balken, einfache · Durchlaufende Träger, Balken, Bogen · Hängewerke und armierte Balken · Einfacher Balken · Balken, durchlaufende · Balken [1] · Armierte Balken · Balken [2] · Balken, armierte · Balken [3]
Meyers-1905: Bälken · Balken · Frei stehende Mauern · Frei Schiff, frei Gut · Frei von Bruch, frei von Beschädigung, frei von Leckage, frei von Verderb · Luft macht frei · Frisch, fromm, froh, frei! · Frei ab · Bildung macht frei · Frei bis zur Adria! · Frei hier · Frei Gut
Pierer-1857: Eingezogene Balken · Erniedrigter Balken · Spanische Balken · Balken [2] · Armirte Balken · Ausgetrumpfte Balken · Balken [1] · Frei [2] · Unfrei Schiff, frei Gut · Frei ab · Frei Schiff, frei Gut · Frei [1]
Roell-1912: Durchgehende (kontinuierliche) Balken
Buchempfehlung
Apuleius
Der goldene Esel. Metamorphoses, auch Asinus aureus
Der in einen Esel verwandelte Lucius erzählt von seinen Irrfahrten, die ihn in absonderliche erotische Abenteuer mit einfachen Zofen und vornehmen Mädchen stürzen. Er trifft auf grobe Sadisten und homoerotische Priester, auf Transvestiten und Flagellanten. Verfällt einer adeligen Sodomitin und landet schließlich aus Scham über die öffentliche Kopulation allein am Strand von Korinth wo ihm die Göttin Isis erscheint und seine Rückverwandlung betreibt. Der vielschichtige Roman parodiert die Homer'sche Odyssee in burlesk-komischer Art und Weise.
196 Seiten, 9.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Große Erzählungen der Spätromantik
Im nach dem Wiener Kongress neugeordneten Europa entsteht seit 1815 große Literatur der Sehnsucht und der Melancholie. Die Schattenseiten der menschlichen Seele, Leidenschaft und die Hinwendung zum Religiösen sind die Themen der Spätromantik. Michael Holzinger hat elf große Erzählungen dieser Zeit zu diesem Leseband zusammengefasst.
- Clemens Brentano Die drei Nüsse
- Clemens Brentano Geschichte vom braven Kasperl und dem schönen Annerl
- E. T. A. Hoffmann Das steinerne Herz
- Joseph von Eichendorff Das Marmorbild
- Ludwig Achim von Arnim Die Majoratsherren
- E. T. A. Hoffmann Das Fräulein von Scuderi
- Ludwig Tieck Die Gemälde
- Wilhelm Hauff Phantasien im Bremer Ratskeller
- Wilhelm Hauff Jud Süss
- Joseph von Eichendorff Viel Lärmen um Nichts
- Joseph von Eichendorff Die Glücksritter
430 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum