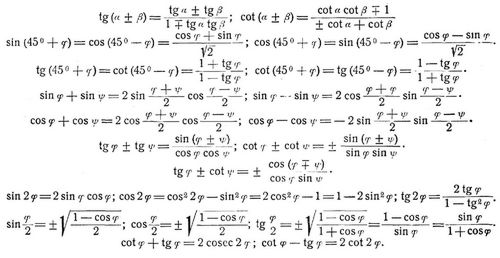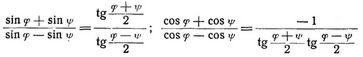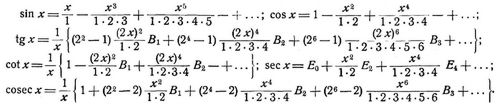Online-Bibliothek

Goniometrie

[596] Goniometrie, die Lehre von Beziehungen zwischen Winkeln (ohne daß diese einem Dreieck anzugehören brauchen); vgl. Trigonometrie.

Die goniometrischen Funktionen (Kreisfunktionen): sin φ = y/r; cos φ = x/r; tg φ = y/x; cot φ = x/y; sec φ = r/x; cosec φ = r/y vermittelst den Zusammenhang zwischen dem Winkel φ und den Seiten x, y, r eines (beliebig großen) rechtwinkligen Dreiecks A B C, welchem derselbe angehört. Der Winkel selbst wird durch das Verhältnis der Bogenlänge M N zum Radius B M[596] gemessen und entweder in Graden angegeben (ein rechter Winkel = 90°, ein flacher = 180°, ein voller = 360°) oder in analytischem Maß (B M = 1, also ein rechter Winkel = π/2, ein flacher = π, ein voller = 2π). – Jede goniometrische Funktion kann durch eine beliebige andre ausgedrückt werden. Es ist:

Die Werte von Sinus und Cosinus liegen zwischen –1 und +1; Tangens und Cotangens nehmen jeden beliebigen Wert an; die Werte von Secans und Cosecans liegen teils zwischen –∞ und –1, teils zwischen +1 und +∞.

Spezialwerte der goniometrischen Funktionen:

Sinus, Tangens, Cotangens, Cosecans sind ungerade, Cosinus und Secans gerade Funktionen.

Vorzeichen der goniometrischen Funktionen in den verschiedenen Quadranten:

Im zweiten Quadranten ist sin (90° + φ) = cos φ; cos (90° + φ) = – sin φ; tg(90° + φ) = – cot φ; cot (90° + φ) = – tg φ; sec (90° + φ) = – cosec φ; cosec (90° + φ) = sec φ. Im dritten Quadranten ist sin (180° + φ) = – sin φ; cos (180°+ φ) = – cos φ; tg (180° + φ) = tg φ; cot (180° + φ) = cot φ; sec (180° + φ) = – sec φ; cosec (180° + φ) = – cosec φ. Im vierten Quadranten ist sin (270° + φ) = – cos φ; cos (270° + φ) = sin φ; tg (270° + φ) = – cot φ; cot (270° + φ) = – tg φ; sec (270° + φ) = cosec φ; cosec (270° + φ) = – sec φ.

Goniometrische Grundformeln:

sin (α ± β) = sin α cos β ± cos α sin β; cos (α ± β) = cos α cos β ± sin α sin β.

[597] Berechnung der goniometrischen Funktionen (in analytischem Maß) mittels der Reihen

Hier sind B₁ B₂ B₃ ... die Bernoullischen, E₀ E₂ E₄ ... die Eulerschen Zahlen. Ueber die Auflösung goniometrischer Gleichungen vgl. [1], Kap. 3. Beispiel: a cos φ + b sin φ = c. Man bestimmt die Hilfsgrößen r und λ mittels tg λ =b/a, r = a/cos λ = b/sin λ. Dann ist cos (φ – λ) = c/r, womit φ gefunden ist.

Die Goniometrie findet vielfach Anwendung in der Algebra (Rechnen mit komplexen Zahlen, Lösung von Kreisteilungsgleichungen, Umformung algebraischer Summen in Produkte zum Zweck der logarithmischen Rechnung, Auflösung von Gleichungen zweiten, dritten und vierten Grades) und in der Trigonometrie und Polygonometrie.

Literatur: [1] Hammer, E., Lehrbuch der ebenen und sphärischen Trigonometrie, 2. Aufl., Stuttgart 1897. – [2] Kleyer, Lehrbuch der Goniometrie, Stuttgart 1886. – [3] Wernicke, Goniometrie, Braunschweig 1888.

Wölffing.