Online-Bibliothek

Diagramm

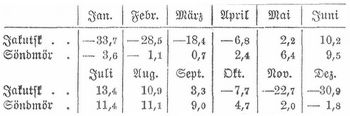
[860] Diagramm (griech.), Linearzeichnung, Entwurf, Abriß, Skizze, gewöhnlich aber die in den Naturwissenschaften und der Statistik übliche graphische Darstellung der Veränderungen, die eine bestimmte Größe mit der Änderung einer zweiten erleidet. Beispielsweise sei der jährliche Gang der Temperatur für ein paar Orte, z. B. Jakutsk in Sibirien (62°2' nördl. Br.) und Söndmör in Norwegen (62°30' nördl. Br.), darzustellen. Die monatlichen Mitteltemperaturen beider Orte sind:

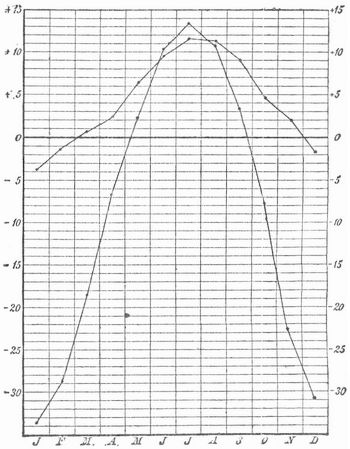
Man trage nun in Fig. 1 auf der Geraden 00 (der Abszissenachse) zwölf gleichlange Teile ab, die den einzelnen Monaten entsprechen und am Fuß der Figur mit J (Januar), F (Februar) etc. bezeichnet sind; durch die Teilpunkte ziehe man Senkrechte zu der Linie 00. Auf der ersten Senkrechten links (der Ordinatenachse) trage man ferner beliebige, aber unter sich gleichlange Teile ab, die den Temperaturgraden entsprechen; dadet werden die Wärmegrade nach oben (+), die Kältegrade nach unken (-) abgetragen.

Fig. 1.

Durch die Teilpunkte ziehe man Parallelen zur Abszissenachse 00. Man gebe nun in der Mitte zwischen je zwei aufeinander folgenden Vertikallinien Punkte an, die von der Abszissenachse 00 um 33,7, 28,5, 18,4, 6,8 Teile nach unten, um 2,2, 10,2, 13,4, ... Teile nach oben entfernt sind, die also die Mitteltemperaturen der einzelnen Monate für Jakutsk angeben, und verbinde je zwei aufeinander folgende Punkte durch eine Gerade oder auch alle Punkte durch eine stetig gekrümmte Linie. Das Steigen und Fallen des so gewonnenen Linienzugs gibt uns rascher als die tabellarische Zusammenstellung ein übersichtliches Bild von dem Gang der Temperatur im Lauf eines Jahres. Zeichnet man in dieselbe Figur auch die Zahlwerte für Söndmör ein (s. die bei -3,6 links anfangende Linie), so hat man ein sehr anschauliches Bild des Kontrastes zwischen den jährlichen Temperaturschwankungen im Innern eines großen Kontinents (Jakutsk) und am Meer (Söndmör).[860]

In ganz ähnlicher Weise lassen sich auch andre meteorologische, physikalische, chemische, statistische und ähnliche Verhältnisse, z. B. in der Medizin der Verlauf des Fiebers, durch ein D. anschaulich machen. Man trägt dann immer eine gewisse Größe (die Zeit, Temperatur etc.) als Abszisse ab, während die zugehörigen Werte der von ihr abhängigen Größe die Ordinaten bilden, deren Endpunkte man durch eine Kurve verbindet. Dies Verfahren ist oft das zweckdienlichste Mittel, Ordnung und Übersicht in die Fülle erfahrungsmäßig gefundener Zahlenwerte zu bringen. Solche Diagramme gestatten häufig noch weitere Schlüsse. Bei dem D., das z. B. der Indikator einer Dampfmaschine auszeichnet, sind die Abszissen proportional dem Weg des Kolbens; die Ordinaten der Kurve aber geben den in jedem Punkte dieses Weges im Zylinder herrschenden Dampfdruck an; die Fläche zwischen Abszissenachse und Kurve ist dann der vom Dampf geleisteten Arbeit proportional.

Fig. 2.

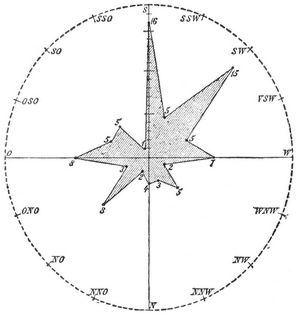
Stellt man irgend eine Bewegung graphisch dar, indem man als Abszissen die Zeit, als Ordinaten die Geschwindigkeiten aufträgt, so drückt die Fläche zwischen Abszissenachse und Kurve den zurückgelegten Weg aus, und wenn man an irgend einem Punkt eine Tangente an die Kurve legt, so ist die trigonometrische Tangente des Winkels, den diese mit der Abszissenachse einschließt, die Beschleunigung. In manchen Fällen, namentlich in der Meteorologie bei Darstellung der Verteilung des Windes auf die einzelnen Himmelsrichtungen, gibt man dem D. eine andre Anordnung: Ist z. B. an einem Orte bei täglich dreimaliger Beobachtung der Windfahne im Lauf eines Monats N. 3 mal, O. 8-, S. 16-, W. 7-, NO. 8-, SO. 5-, NW. 5-, SW. 15-, NNO. 2-, NNW. 3-, SSO. 1-, SSW. 5-, ONO. 3-, OSO. 5-, WNW. 2- und WSW. 5 mal beobachtet worden, so kann man dies bildlich darstellen, indem man in einem Kreis 8 Durchmesser zieht, die den 16 Richtungen der Windrose entsprechen (Fig. 2, wo aber nur 2 Durchmesser, von den andern bloß die Endpunkte angegeben sind). Auf jedem Halbmesser trägt man dann vom Mittelpunkt aus so viel gleichgroße Teile ab, als die Zahl der Beobachtungen ist, die auf die betreffende Windrichtung kommt. Die Endpunkte (denen in der Figur die Zahlen beigeschrieben sind) werden hierauf geradlinig verbunden. Die Figur (in der auf dem nach S. gerichteten Halbmesser auch der Maßstab angegeben ist) zeigt uns, namentlich wenn wir sie durch Schraffieren besser sichtbar machen, sehr deutlich das Vorherrschen der Winde aus dem Quadranten von S. nach W. Vgl. Statistik (Darstellungsmethoden). D. des Hipparchos ist die Zeichnung des Standes der Sonne, des Mondes und der Erde bei Finsternissen, nebst den dazu gehörigen Linien, durch die Hipparchos die Entfernung der Sonne und des Mondes von der Erde sowie die Parallaxe dieser beiden Himmelskörper zu finden lehrte. Über Blütendiagramme s. Blüte, S. 87.