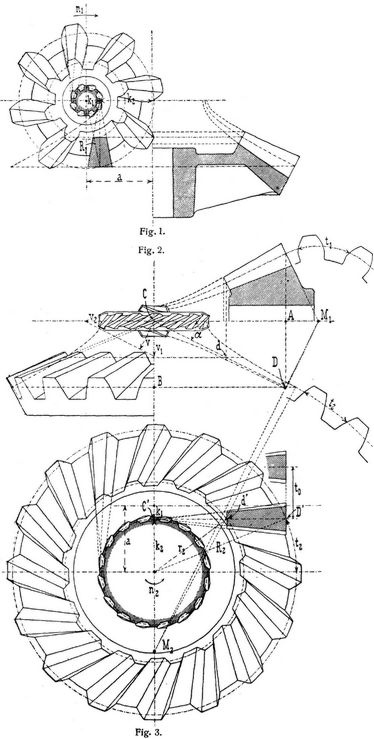
Hyperbelräder
[163] Hyperbelräder sind an Stelle von Kegelrädern anzuwenden, wenn die Wellen beider Zahnräder aneinander vorbeigehen müssen. Bei Uebertragung großer Kräfte vermeidet man sie, weil die Zähne sich nicht nur in der Richtung vom Fuß zum Kopf reiben, sondern auch in der Breitenrichtung aneinander gleiten und darum bei starkem Zahndruck großen Reibungsverlust und schnelle Abnutzung verursachen. Die Zähne sind der Breite nach geradlinig verjüngt, stehen aber nicht zentrisch, sondern schräg.
Spannt man zwischen zwei gleichen konaxialen Reifen parallele Fäden, so daß diese zunächst in einer Zylinderfläche liegen, und dreht den einen Reifen um seine Achse um 180°, so bilden die Fäden eine Kegelfläche; dreht man aber weniger als 180°, so ist die von geradlinigen Fäden umschriebene Fläche ein Hyperboloid, weil ihre Meridianschnitte Hyperbeln darstellen. Der kleinste Kreis in der Mitte zwischen beiden Reifen heißt Kehlkreis. Die geraden Linien der gespannten Fäden geben die gerade Berührungslinie zweier aneinander gelegten Hyperboloide und zugleich die Richtung der Zähne eines Hyperbelrades an. Läßt man zwei sich berührende Hyperboloide um ihre Achten rotieren, indem man sich anstatt der Fäden Zähne denkt, so muß die Geschwindigkeit v senkrecht zur geraden Berührungslinie für beide Räder dieselbe sein. In der Umfangsrichtung dagegen sind die Zahngeschwindigkeiten v1 und v2 verschieden, je nach dem Winkel zwischen der Geraden und den Umfangen der beiden Räder. Es sei weiterhin vorausgesetzt, daß die Achsen einen Winkel von 90° bilden und im Abstande a (Fig. 1 und 3) aneinander vorbeigehen, daß ferner das Uebersetzungsverhältnis Z1 : Z2 = n2 : n1 (z.B. = 1 : 2 in der Figur) gegeben sei. In Fig. 2 geht, der Bildebene parallel (also unverkürzt), die gerade Berührungslinie C D der Hyperboloide von dem scheinbaren Schnittpunkte C der Achsen aus, und zwar so, daß D A : D B = Z1 : Z2 ist. Durch die Annahme des Punktes D ist die Größe der Räder bestimmt. Am kleinsten werden die Kehlkreise mit den Radien k1 und k2.[163] Nach Fig. 2 (unterhalb des in Ansicht gezeichneten, obenaufliegenden Kehlrades) sind deren Umfangsgeschwindigkeiten v2 = v/sin a und v1 = v/cos α, folglich ist:
und
In dem Verhältnis k1 : k2 ist die Achsenentfernung a in Fig. 1 und 3 zu teilen. Als Tangenten an den so erhaltenen Kehlkreisen bestimmen die Projektionen von C D in Fig. 1 und 3 die Richtungen der Zähne. In dem Abstande des in Fig. 3 projizierten Punktes D' von der Achse des Rades erhält man den Radius R2 des äußeren Teilkreises. Hat man weiter den Punkt d in Fig. 2, der Zahnbreite D d entsprechend, angenommen, so ergibt sich aus der Projektion d' in Fig. 3 der Radius r2 des inneren Teilkreises. Trägt man diese Radien R2 und r2 und außerdem noch beliebige andre ebenso konstruierte Radien in Fig. 2 ein, so erhält man die Punkte der Hyperbel des zweiten Rades und ebenso aus Fig. 1 die des ersten Rades. Senkrecht zur Zahnrichtung C D' in Fig. 3 ist die für beide Räder gleiche und für die Zahnstärke maßgebende Teilung t0 = 2 π + C' D'/Z2 aufgetragen. Weil nun aber die Zähne am äußeren Umfang schräg unter dem Winkel, den C' D' mit R2 bildet, abgeschnitten sind, wird die am Rade meßbare Teilung t2 im Verhältnis R2 : C' D' größer als t0. Entsprechend ergibt sich aus Fig. 1 die Teilung t1 für das kleine Rad. Hiernach werden die Umfangsteilungen beider Räder verschieden. Errichtet man in Fig. 2 auf C D in D ein Lot, so erhält man in dessen Schnittpunkten auf den Achsen die Spitzen M1 und M2 der Kegel, welche die Zahnkränze außen begrenzen. In der Abwicklung dieser Kegel (Fig. 2, rechts) sind die Zahnkurven zu konstruieren. Hiernach lassen sich die Begrenzungslinien der Zähne in die Räder einzeichnen. An Stelle der Hyperboloide, welche die Kopfflächen und den Zahnboden bilden, wird man Kegelflächen annehmen.
Die in den Figuren eingezeichneten Kehlkreisräder sind Schraubenräder. Wegen der starken Steigung der Zähne am kleineren Rade wird dieses das größere nicht zu treiben vermögen, wohl aber umgekehrt von dem größeren getrieben werden können. – Zur Anwendung kommen hyperbolische Räder beispielsweise an den Spindelbänken für Baumwollspinnerei (s. Bd. 1, S. 610).
Literatur: [1] Reuleaux, Der Konstrukteur, Braunschweig 1882–89, S. 549–554. – [2] Keller, Triebwerke, München 1904, S. 163–170. – [3] Herrmann-Weisbach, Mechanik, Braunschweig 1876, 3. Teil, 1. Abt., S. 228–237.
Lindner.
Buchempfehlung
Anonym
Schi-King. Das kanonische Liederbuch der Chinesen
Das kanonische Liederbuch der Chinesen entstand in seiner heutigen Textfassung in der Zeit zwischen dem 10. und dem 7. Jahrhundert v. Chr. Diese Ausgabe folgt der Übersetzung von Victor von Strauß.
298 Seiten, 15.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Romantische Geschichten II. Zehn Erzählungen
Romantik! Das ist auch – aber eben nicht nur – eine Epoche. Wenn wir heute etwas romantisch finden oder nennen, schwingt darin die Sehnsucht und die Leidenschaft der jungen Autoren, die seit dem Ausklang des 18. Jahrhundert ihre Gefühlswelt gegen die von der Aufklärung geforderte Vernunft verteidigt haben. So sind vor 200 Jahren wundervolle Erzählungen entstanden. Sie handeln von der Suche nach einer verlorengegangenen Welt des Wunderbaren, sind melancholisch oder mythisch oder märchenhaft, jedenfalls aber romantisch - damals wie heute. Michael Holzinger hat für den zweiten Band eine weitere Sammlung von zehn romantischen Meistererzählungen zusammengestellt.
- Novalis Die Lehrlinge zu Sais
- Adelbert von Chamisso Adelberts Fabel
- Jean Paul Des Feldpredigers Schmelzle Reise nach Flätz
- Clemens Brentano Aus der Chronika eines fahrenden Schülers
- Friedrich de la Motte Fouqué Eine Geschichte vom Galgenmännlein
- E. T. A. Hoffmann Der goldne Topf
- Joseph von Eichendorff Das Marmorbild
- Ludwig Achim von Arnim Die Majoratsherren
- Ludwig Tieck Die Gemälde
- Wilhelm Hauff Die Bettlerin vom Pont des Arts
428 Seiten, 16.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum