Online-Bibliothek

Linse [1]

[169] Linse, in der Optik ein von zwei gegenüberstehenden Kugelflächen begrenzter durchsichtiger Körper (über Zylinderlinsen s. S. 171 und Brille, über Kristallinse des Auges s. Auge). Die durch die beiden Kugelmittelpunkte gehende Gerade heißt Achse der Linse.

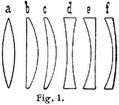
Man unterscheidet Konvexlinsen oder Sammellinsen und Konkavlinsen oder Zerstreuungslinsen; erstere, in der Mitte dicker als am Rande (vgl. Fig. 1), sind entweder bikonvex (a) oder plankonvex (b) oder konkavkonvex (c), letztere in der Mitte dünner als am Rande (Fig. 1), sind entweder bikonkav (d) oder plankonkav (e) oder konvexkonkav (f). Als optische Gläser dienen besonders das Kronglas (s.d.) und verschiedene Sorten Flintglas (s.d.), über deren Lichtbrechung und Farbenzerstreuung sich in [1] eine Zusammenstellung der Messungen von Fraunhofer, v. d. Willigen, Maskart, Langley. F. Vogel und G. Müller nebst reichlichen Literaturangaben findet. Teils einzeln, teils zu Systemen verbunden, bilden sie die wichtigsten optischen Instrumente (vgl. a. Fernrohr, Lupe, Mikroskop u.s.w.). In diesen Liniensystemen sind die Linsen so verbunden, daß sie eine gemeinsame Achse haben. Sie dienen, mit etwaiger Ausnahme der Scheinwerfer, der Beleuchtungslinsen u. dergl., alle dem Zweck der optischen Abbildung, der Entwerfung von Bildern gegebener Gegenstände. Jedem Punkte des Objektraums, in welchem die das System passierenden Strahlen entspringen, entspricht ein konjugierter Punkt des Bildraums, in welchen die Strahlen aus dem System austreten. Soweit die aus der sphärischen Begrenzung der Linsen und aus der Farbenzerstreuung entspringenden Fehler gehoben sind (vgl. Aberration, sphärische und chromatische, Achromasie, Aplanatisch), wird das ganze vom einen der konjugierten Punkte (die Rollen sind vertauschbar) ausgehende Strahlenbüschel so im System gebrochen, daß es sich im andern zum zweitenmal schneidet. Liegt dieser zweite Schnittpunkt nicht auf den austretenden Strahlen selbst, sondern auf deren Rückwärtsverlängerung, so heißt er, zum Unterschied von reellen Bildern, virtuell oder imaginär. So sind die Bilder der Camera obscura und der Laterna magica reell, diejenigen der Lupen und der Okulare virtuell; erstere dienen der objektiven Darstellung, etwa auf einem Schirm, letztere der subjektiven Darstellung der Abbildung, nur wahrnehmbar für ein in dem Strahlengang befindliches Auge.

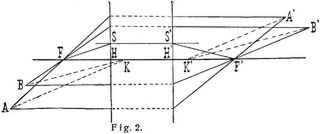
Die geometrische Theorie der Linsen und Linsensysteme bedient sich, besonders seit Gauß [2]–[5], gewisser ausgezeichneter Punkte, Kardinalpunkte, und Ebenen zur konstruktiven und zur analytischen Darstellung des Zusammenhangs zwischen Bild und Gegenstand. Wir geben, unter Verweis auf die bezeichnete Literatur und auf die Behandlung der geometrischen Optik in [6] und [7], eine kurze Erklärung der Grundbegriffe an der Hand von Fig. 2. Da die von einem Punkte A oder B des Objektraums ausgehenden Strahlen sich im Punkte A' oder B' des Bildraums schneiden und umgekehrt, so ist jeder Strecke A B des einen Raums eine Strecke A' B' des andern konjugiert, die entsprechenden Gebilde beider Räume sind kollinear. Auch zwei sich schneidende Strahlen und damit eine Ebene des einen Raums sind konjugiert zwei Strahlen und ihrer Ebene des andern Raums. Wegen des symmetrischen Baus des Systems gegen seine Achse muß insbesondere jeder zur Achse senkrechten Ebene wieder eine solche senkrechte [169] Ebene konjugiert sein. Der unendlich fernen senkrechten Ebene des einen Raums ist im andern im allgemeinen eine nicht im Unendlichen liegende Ebene parallel. Diese heißt Brennebene, ihr Schnittpunkt mit der Achse Brennpunkt (Fokus). Jeder achsenparallele Strahl des einen Raums geht nach der Brechung im Linsensystem durch den Brennpunkt des andern Raums und umgekehrt. Denkt man sich eine beliebige achsenparallele Gerade S S' jedem der beiden Räume zugehörig, so entsprechen dieser Doppelgeraden als konjugierte zwei durch die Brennpunkte F und F' gehende Gerade, deren Schnittpunkte S und S' mit der ersten ein Paar konjugierter Punkte vorstellen. Die durch S und S' gelegten, zur Achse senkrechten Ebenen sind ebenfalls konjugiert und haben die Besonderheit, daß jeder Figur der einen Ebene eine gleichgerichtete kongruente der andern Ebene konjugiert ist. Diese zwei Ebenen heißen die Hauptebenen des Systems, ihre Schnittpunke H und H' mit der Achse heißen die Hauptpunkte. Die Abstände der Brennpunkte von den Hauptpunkten H F = f und H' F' = f' heißen die Brennweiten des Systems. Sie sind gleich, wenn die Strahlen des Objektraums und des Bildraums im gleichen Mittel, etwa beide in Luft, verlaufen. Durch die beiden Brennpunkte und die Hauptpunkte ist ein Linsensystem so definiert, daß zu jedem Punkt A des einen Raumes der konjugierte A' des andern sich ermitteln läßt, graphisch, indem man von A zwei Strahlen zieht, den einen durch F bis zur Hauptebene H', den andern achsenparallel bis zur Hauptebene H', die konjugierten Strahlen gehen dann der eine achsenparallel, der andre durch F' und schneiden sich in A', analytisch, indem man die Achsen abstände der konjugierten Punkte A und A' mit y und y', ihre Abstände von den Hauptebenen mit a und a' bezeichnet, d.h. a : f = (y + y') : y' und a' : f' = (y + y') : y', woraus sich ergibt

(f : a) + (f' : a') = 1.

1.

Denkt man sich die beiden Räume um den Abstand der beiden Hauptebenen gegeneinander verschoben, so kommen die konjugierten Gebilde in perspektivische Lage; jede Verbindungslinie zweier konjugierter Punkte schneidet die Achse im gleichen Punkte K, der bei der Aufhebung der Verschiebung die beiden Knotenpunkte K und K' liefert. Wenn f = f', fällt H mit K, H' mit K' zusammen.

Bei einer einzelnen bikonvexen oder bikonkaven Linse geringer Dicke fallen Hauptpunkte und Knotenpunkte im Innern des Glases nahe in einen Punkt zusammen, den optischen Mittelpunkt der Linse. Jeder durch den optischen Mittelpunkt der Linse gehende Strahl hat beim Eintritt und Austritt gleiche Richtung; für die Linse bekommt daher die Gleichung 1. die Form α + α' = φ, wenn man mit α, α' und φ die reziproken Werte von a, a' und f bezeichnet, und verbindet sich mit der zweiten

γ =y' : y = a' : a,

2.

wobei γ das lineare Größenverhältnis zweier in den konjugierten Abständen a und a' von der Linse befindlichen konjugierten Gebilde bezeichnet. Für die Brennweite f der Linse ist der Brechungsindex n des Glases und sind die Krümmungsradien r und r' der begrenzenden Kugelflächen maßgebend. Man erhält, falls die Radien konvexer Flächen positiv, diejenigen konkaver negativ gezählt werden, die in allen elementaren Lehrbüchern der Physik abgeleitete Gleichung: φ = (n – 1) (ρ + ρ'), wobei ρ und ρ' die reziproken Werte von r und r' bezeichnen, genauer nach [7]:

unter Berücksichtigung der Linsendicke d. Die Größe φ = 1 : f heißt auch die Stärke der Linse. Bei allen Konkavlinsen wird f negativ, d.h. der Brennpunkt, nach welchem achsenparallele Strahlen nach dem Durchgang konvergieren, liegt auf der Seite des Objektraums, die gebrochenen Strahlen divergieren von dem virtuellen Bildpunkt des unendlich fernen Punktes aus, für die Konvexlinsen ist f positiv.

Bei gegebenem reellen Objekt können a und α nur positiv sein; die Gleichung 1. liefert daher für Konkavlinsen nur negative Werte von α' und a, und zwar ihrem absoluten Werte nach sind α' > α daher α' < α; die Bildvergrößerung γ wird nach Gleichung 2. < 1 und negativ, d.h. die Konkavlinsen liefern nur virtuelle verkleinerte aufrechte Bilder reeller Objekte zwischen den Abständen α' = 0 und α' = –f.

Für die Konvexlinsen sind sechs verschiedene Fälle zu unterscheiden:

1. a = ∞ gibt α' = f, γ = ∞ klein. Da die astronomischen Objekte eine im Vergleich mit terrestrischen Objekten ∞ große Ausdehnung haben, so bleibt die Bildgröße durch die Gleichung 2., unbestimmt, sie ergibt sich mit Hilfe der ungebrochen durch den optischen Mittelpunkt gehenden Strahlen als perspektivisches Gegenbild des Objekts entworfen auf die Brennebene. Zum Beispiel das Sonnenbildchen am Brennpunkt hat den Radius f tg 16', weil der Radius der Sonnenscheibe unter dem Winkel von 16' erscheint.

2. a > 2f gibt a' < 2f, aber > f und γ < 1. Das Objektiv einer Camera obscura, auf einen mehr als 2f entfernten Gegenstand gerichtet, entwirft von demselben ein umgekehrtes reelles Bild auf die zwischen den Abständen f und 2f befindliche Wand.

3. a = 2f gibt a' = 2f = 2/ und γ = 1. In den sogenannten terrestrischen Fernrohren hat die Umkehrungslinse den Zweck, von dem rellen, durchs Objektiv entworfenen umgekehrten Bild im Abstände 4f von diesem ein gleichgroßes aufrechtes Bild zu entwerfen.

4. a < 2f aber > f gibt a' > 2f und γ > 1. Das ist die Wirkung der Objektivlinse eines zusammengesetzten Mikroskops sowie des Sonnenmikroskops und der Zauberlaterne.

5. a = f gibt a' = ∞ und γ = ∞, Wirkung der Scheinwerfer und Leuchtturmlinsen.[170]

6. a < f gibt a' negativ und absolut > a, γ > 1, die Lupe führt die Strahlen so zum Auge, als ob dieselben von einem in Sehweite befindlichen großen Bilde herkämen.

Diese Zahl der Fälle der Wirkung der Konkav- und Konvexlinsen erweitern sich bei der Wirkung in den Linsensystemen, insofern hier auch negative Werte von a auftreten, so oft eine Linse in den Gang von Strahlen eingeschaltet wird, die sich noch nicht zu reellen Bildern vereinigt haben. Das Okular des galileischen Fernrohrs liefert hierfür ein Beispiel (s. Fernrohr).

Ueber Herstellung der Linsen s. Glas, Bd. 4, S. 546, und Schleifen (Abschnitt Glas).

Zylinderlinsen sind ganz oder teilweise durch Zylinderflächen begrenzte optische Linsen. Ist eine Linse durch zwei konvexe Zylinderflächen mit parallelen Mantellinien begrenzt, so werden parallel auf sie auffallende Strahlen nach einer Brennlinie gebrochen. Man bedient sich solcher Linsen bei den Spektralapparaten (s. Spektralanalyse), teils um die Brennlinien auf dem Spalt des Spektralapparats zu entwerfen und denselben dadurch sehr intensiv zu beleuchten, teils um die punktförmigen Bilder der Fixsterne, denen ein Spektrum von verschwindender Breite entspricht, in linsenförmige Bilder zu verzerren und dadurch Spektralbänder der Fixsterne zu erzeugen. Wird nur letzterer Zweck verfolgt, so dient die Zylinderlinse als Okularlinse des Spektralapparats. Eine zweite Verwendung finden zylindrisch geschliffene Linsen als Brillengläser für astigmatische Augen (s. Astigmatismus); hierbei kann die eine Fläche der Linse eben oder sphärisch, die andre zylindrisch geschliffen sein. Ueber die geometrisch-optischen Gesetze des Strahlganges vgl. Reusch, Theorie der Zylinderlinsen, Leipzig 1868.

Literatur: [1] Landolt u. Börnstein, Physikal. Tabellen, 3. Aufl., Berlin 1905, S. 623 u. 624. – [2] Gauß, Dioptrische Untersuchungen, Göttingen 1841, Abh. der Göttinger Gesellschaft der Wissensch. 1838–1843. – [3] Neumann, C., Die Haupt- und Brennpunkte des Linsensystems, Leipzig 1866. – [4] Reusch, Konstruktionen zur Lehre von den Haupt- und Brennpunkten eines Linsensystems, Leipzig 1870. – [5] Zech, P., Elementare Behandlung von Linsensystemen, mathem.-naturwissensch. Mitteilungen von Böklen, Tübingen 1884, Bd. 2, S. 9–28. – [6] Heath, R.S., A treatise on geometrical optics, Cambridge 1887, deutsch von Kanthack, Berlin 1893. – [7] Czapski, Theorie der optischen Instrumente nach Abbe, Breslau 1893 (auch im Bd. 2, 1. von Winkelmanns Handbuch der Physik), S. 23, 25 u. 43, mit zahlreichen Literaturnachweisen, 2. Aufl., Leipzig 1904, S. 79 ff.

Aug. Schmidt.

Fig. 1.

Fig. 2.