Doppelbrechung
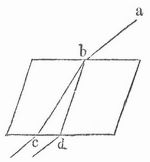
[122] Doppelbrechung, Eigenschaft aller amorphen sowie der nicht zum regulären System gehörigen kristallisierten Körper, einen in sie eindringenden Lichtstrahl (a b) in zwei Strahlen (b c und b d) zu trennen (Fig. 1).
Sie ist bedingt durch die Verschiedenheit der Diëlektrizitätskonstante (s. d.) nach verschiedenen Richtungen, da von dieser Konstante die Fortpflanzungsgeschwindigkeit des Lichtes, somit auch dessen Brechung (s. d.) abhängt. Körper, die nach allen Richtungen mit gleichen optischen Eigenschaften begabt sind, nennt man isotrop, die übrigen heißen anisotrop oder heterotrop.
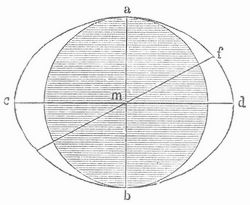
Werden in einem Punkt eines isotropen Körpers (z. B. Glas) beliebig gerichtete elektrische Schwingungen erregt, so pflanzen sich dieselben zwar mit einer geringern Geschwindigkeit fort als im freien Äther, aber nach allen Seiten mit der gleichen Geschwindigkeit und erzeugen rings um jenen Punkt kugelförmige Wellen. Man sagt daher, daß die Wellenfläche der isotropen Mittel eine Kugel sei. Anders ist es in einem anisotropen Körper. Als Beispiel diene der Kalkspat, der leicht in großen klaren Spaltungsstücken von der Form eines Rhomboeders (Fig. 2) erhalten wird. Rings um die Achse (Hauptachse) des Kristalls a b, welche die zwei stumpfen Ecken miteinander verbindet, sind die Flächen, Kanten und Ecken symmetrisch geordnet. Eine jede durch die Achse gelegte Ebene wird Hauptschnitt genannt.
In ähnlich symmetrischer Weise sind nun auch die Moleküle des Kalkspats gebaut zu denken. Jedes derselben besitzt eine vor allen andern Richtungen ausgezeichnete Hauptachse, die zur Kristallachse parallel liegt, und übt daher auf Lichtschwingungen, die zu dieser Hauptachse parallel sind, einen andern Einfluß aus als auf solche, die zu dieser Achse senkrecht oder unter irgend einem Winkel geneigt sind. (Früher nahm man an, daß die Art der Zusammenlagerung der Moleküle die D. bedinge. Durch Auffindung flüssiger Kristalle [s. d.] ist diese Annahme hinfällig geworden.) Nun stelle in Fig. 3 die Ebene der Zeichnung einen Hauptschnitt eines Kalkspatkristalls vor und a b die Achsenrichtung. In dem Punkt m mögen Schwingungen erregt werden, die teils in der Ebene des Hauptschnittes erfolgen, teils zu ihr senkrecht stehen; die letztern pflanzen sich nach allen Seiten mit der nämlichen Geschwindigkeit fort, weil für alle Richtungen senkrecht zur Achse die Diëlektrizitätskonstante gleich ist, und erzeugen die in der Figur angedeutete kreisförmige Welle.
Die in der Ebene des Hauptschnittes liegenden Schwingungen aber pflanzen sich mit verschiedenen Geschwindigkeiten fort, je nach dem Winkel, den sie mit der Achse bilden. Schwingungen z. B., die nach a b parallel der Achsenrichtung selbst erfolgen, geben Anlaß zu einem Strahl m d, der in der nämlichen Zeit, in der die zur Achse senkrechten Schwingungen den Halbmesser jener Kreiswelle durchlaufen, eine größere Strecke m d zurücklegt, weil beim Kalkspat die zur Achse parallelen Schwingungen eine geringere Verzögerung erfahren als die zur Achse senkrechten. Schwingungen dagegen, die nach c d gerichtet sind, senden, weil sie senkrecht zur Achse stehen, einen Strahl m a aus, der in der gedachten Zeit nur bis zu jenem Kreis vordringt. Solchen [122] Strahlen endlich, deren Schwingungen einen schiefen Winkel mit der Achse bilden, wird eine Fortpflanzungsgeschwindigkeit (z. B. m f) zukommen, die kleiner ist als m d, aber größer als m a. Die im Hauptschnitt gelegenen Schwingungen erzeugen demnach eine Welle von elliptischem Umriß a b c d, welche die Kreiswelle, die den zum Hauptschnitt senkrechten Schwingungen entspricht, an den Achsenendpunkten a und b berührt. Da für alle Hauptschnitte das Nämliche gilt, so braucht man nur die Fig. 3 um die Achse ab gedreht zu denken, um die Wellenfläche zu erhalten, die für die beiden genannten Schwingungsrichtungen maßgebend ist. Diese Wellenfläche besteht aus zwei Schalen, einer Kugel für die zur Achse senkrechten Schwingungen u. einem abgeplatteten Rotationsellipsoid von orangeähnlicher Gestalt, das die Kugel umschließt und sie an den Endpunkten der Achse berührt, für die zur Achse nicht senkrechten Schwingungen.
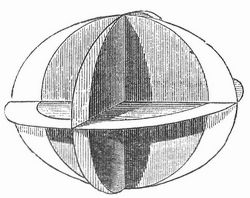
Die Figur 4 zeigt drei zueinander rechtwinkelige Durchschnitte, nämlich zwei Hauptschnitte und einen zur Achse senkrechten Schnitt, zu einem leichtverständlichen Modell der Wellenfläche zusammengefügt.
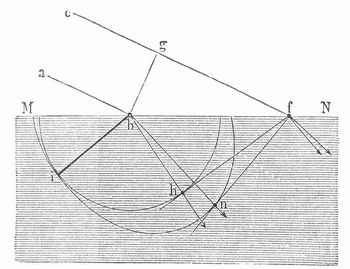
Nun werde die Oberfläche MN (Fig. 5) eines Kalkspatkristalls von einem Bündel paralleler Lichtstrahlen a b e f getroffen; zieht man von b aus, wo die Oberfläche von der Lichtbewegung zuerst erreicht wird, eine Senkrechte b g zur Strahlenrichtung, so stellt diese das zu dem Lichtbündel gehörige-ebene Wellenstückchen vor, in dem sich sämtliche Ätherteilchen gleichzeitig im nämlichen Polarisationszustand befinden. Indem die Welle b g gegen die Kristalloberfläche fortschreitet, werden die zwischen b und f liegenden Ätherteilchen der Reihe nach von der Zustandsänderung ergriffen, und jedes entsendet eine Welle in den Kristall hinein.
Der Einfachheit wegen werde angenommen, daß die Einfallsebene, d.h. die Ebene der Zeichnung, zugleich ein Hauptschnitt des Kristalls sei. Jeder einfallende Lichtstrahl bestehe aus zwei gleich hellen Strahlen, von denen der eine im Hauptschnitte, der andre senkrecht dazu schwingt. Letztere Schwingungen, die senkrecht zur Kristallachse b i erfolgen, werden sich, während die Welle b g von g bis f fortschreitet, im Kristall von b aus zu einer kreisförmigen Welle i h ausgebreitet haben, deren Halbmesser b h sich zu g f verhält wie die Fortpflanzungsgeschwindigkeit dieser Art Schwingungen im Kristall zur Fortpflanzungsgeschwindigkeit des Lichts in der Luft. Von jedem zwischen b und f gelegenen Punkte der Kristallfläche wird gleichzeitig eine Kreiswelle ausgegangen sein, deren Halbmesser jedoch um so kleiner ist, je später der zugehörige Punkt von der einfallenden Welle erfaßt wird. Alle diese Kreiswellen sind in dem Augenblick, in dem der Punkt f von der einfallenden Welle erreicht wird, bis zur Linie f h vorgedrungen, welche die gemeinsame Berührungslinie sämtlicher Kreiswellen ist. Die Linie f h stellt demnach die ebene Welle vor, die sich in den Kristall hinein fortpflanzt, und die von b nach dem Berührungspunkt h gezogene Gerade b h gibt die zugehörige Richtung der gebrochenen Strahlen an. Da die bei dieser Zeichnung in Anwendung gekommene Wellenschale wie bei den einfach brechenden (isotropen) Mitteln kugelförmig ist, so befolgt ein Strahl, der senkrecht zum Hauptschnitt schwingt, das gewöhnliche Snelliussche Brechungsgesetz (s. Brechung, S. 367). Will man sich in ähnlicher Weise von der Brechung der im Hauptschnitt schwingenden Strahlen Rechenschaft geben, so hat man, wenn b i die Richtung der Achse ist, um b den Umriß n i der elliptischen Wellenschale und von f aus die Berührungslinie f n an denselben zu ziehen; diese Linie gibt alsdann die Lage der gebrochenen Welle und die von b aus nach dem Berührungspunkt n gezogene Gerade die zugehörige Strahlenrichtung an. Dieser Strahl befolgt nicht das gewöhnliche, sondern infolge der ellipsoidischen Gestalt seiner Wellenfläche ein viel verwickelteres Brechungsgesetz. Erfolgen die Schwingungen der auftreffenden Lichtstrahlen weder im Hauptschnitt, noch senkrecht dazu, sondern in einer beliebigen dazu geneigten Richtung, so tritt dasselbe ein, was geschieht, wenn wir z. B. einen Stahlstab von rechteckigem Querschnitt in Schwingungen schräg zu den Querschnittsseiten versetzen wollen. Solche Schwingungen sind nicht möglich, es entstehen vielmehr zwei gleichzeitig stattfindende Schwingungen, die einen parallel der kürzern, die andern parallel der längern Querschnittsseite, deren Stärke sich ergibt, wenn wir den mitgeteilten Stoß nach diesen beiden Richtungen entsprechend dem Satz vom Kräfteparallelogramm zerlegen. Genau ebenso findet im Fall der beliebig gerichteten Lichtschwingungen eine Zerlegung derselben nach dem Parallelogrammgesetz in eine solche im Hauptschnitt und eine solche senkrecht dazu statt den Richtungen größter und kleinster Diëlektrizitätskonstante, die wegen der anisotropen Beschaffenheit der Moleküle allein möglich sind. Gleiches gilt vom natürlichen, nicht polarisierten Lichte, das aus Strahlen von allen möglichen Schwingungsrichtungen zusammengesetzt gedacht werden kann. Man sieht also, daß ein auf einen Kalkspatkristall treffender natürlicher Lichtstrahl (a b) im allgemeinen in zwei mit ungleicher Geschwindigkeit sich fortpflanzende Strahlen zerlegt wird, einen gewöhnlich gebrochenen oder ordinären (b h) und einen außergewöhnlich gebrochenen oder extraordinären Strahl (b n); beide sind vollständig polarisiert, und zwar schwingt dieser im Hauptschnitt, jener aber senkrecht zum Hauptschnitte. Da in der Richtung der Achse nur eine einzige Fortpflanzungsgeschwindigkeit stattfindet, so erleidet ein längs der Achse in den Kristall eindringender natürlicher Lichtstrahl keine Zerlegung[123] Jede solche Richtung in einem doppelbrechenden Kristall, längs der keine D. erfolgt, heißt eine optische Achse. Alle Kristalle des quadratischen und hexagonalen Systems (zu welch letzterm der Kalkspat gehört) haben nur eine einzige optische Achse, die mit ihrer kristallographischen Hauptachse zusammenfällt, und heißen daher optisch-einachsig. Solche Kristalle, bei denen sich die außergewöhnlichen Strahlen schneller fortpflanzen als die gewöhnlichen, bei denen also die ellipsoidische Wellenschale die Kugelwelle umschließt, wie Kalkspat, Turmalin, salpetersaures Natron etc., heißen einachsig-negativ. Wird dagegen das Ellipsoid von der Kugelwelle umschlossen, oder haben die gewöhnlichen Strahlen die größere Fortpflanzungsgeschwindigkeit, so heißen die Kristalle einachsig-positiv, z. B. Bergkristall oder Quarz, Zirkon, Zinnstein, Eis etc.
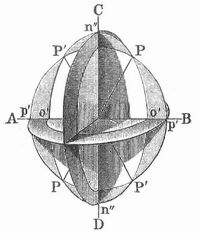
Auch in den Kristallen der drei übrigen Systeme pflanzen sich zwei zueinander senkrecht polarisierte Strahlen mit ungleicher Geschwindigkeit fort, wovon jedoch keiner im allgemeinen dem gewöhnlichen Brechungsgesetz gehorcht. Die Wellenfläche (Fig. 6) besteht auch hier aus zwei Schalen, deren eine von der andern ganz umschlossen wird, so jed och, daß beide in vier Punkten PPP'P' zusammenhängen. Um jeden dieser Punkte zeigt die äußere Schale eine trichterförmige Einsenkung n´´Pp´, der sich eine trichterförmige Hervorragung o´PP´ der innern Schale entgegenstreckt. Die eigentümliche Gestaltung der Wellenfläche in der Nähe dieser »singulären« Punkte gibt zu merkwürdigen Erscheinungen Veranlassung. Ein natürlicher Strahl, der sich im Kristall in der Richtung PP oder P´P´ fortflanzt, breitet sich beim Austritt in einen hohlen Strahlenkegel aus (äußere konische Refraktion); und trifft ein Strahl derart auf den Kristall, daß die innerhalb desselben ihm zugehörige Wellenebene die Wellenfläche längs des Randes jenes Trichters berührt, so löst sich der Strahl im Kristall in einen Strahlenkegel auf, der in Form eines hohlen Strahlenzylinders aus dem Kristall austritt (innere konische Refraktion). Eine Senkrechte, die man sich vom Mittelpunkt der Wellenfläche auf eben genannte Wellenebene gefällt denkt, heißt eine optische Achse des Kristalls, und da zwei solche Richtungen, die übrigens von den Richtungen PP und P'P' nur wenig abweichen, vorhanden sind, so nennt man diese Kristalle optisch-zweiachsig. Die Gerade CD, die den spitzen Winkel der optischen Achsen halbiert, heißt die Mittellinie. Die Ebene der optischen Achsen ist auch diejenige der größten und kleinsten Diëlektrizitätskonstante, die den Richtungen AB und CD entsprechen. Positiv-zweiachsig nennt man einen Kristall, wenn die kleinste, negativ zweiachsig, wenn die größte Elastizität in der Richtung der Mittellinie vorhanden ist.
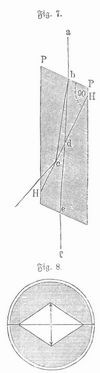
Indem die D. jedes natürliche Lichtbündel in zwei zueinander senkrecht polarisierte zerlegt, bietet sie ein vortreffliches Mittel zur Herstellung polarisierten Lichtes, wenn man nur dafür Sorge trägt, daß das eine der beiden durch D. entstandenen Lichtbündel beseitigt wird, weil es sonst, mit dem andern sich vermischend, wieder unpolarisiertes Licht geben würde. Dies geschieht durch das Nicolsche Prisma (Fig. 7), das aus einer durch Spaltung erhaltenen Kalkspatsäule hergestellt wird, an die man statt der natürlichen Endflächen, die mit den stumpfen Seitenkanten PH einen Winkel von 71° bilden, neue Flächen PP anschleift, deren Winkel mit diesen Kanten 68° beträgt. Das Prisma wird durch einen zu den neuen Endflächen senkrechten Schnitt HH entzweigesägt und die Schnittflächen, nachdem sie poliert sind, mittels Kanadabalsams wieder zusammengekittet. Trifft nun ein natürlicher Lichtstrahl a b auf die Vorderfläche PP, so spaltet er sich in einen gewöhnlich gebrochenen Strahl b c und einen ungewöhnlich gebrochenen b d. Der erstere, dessen Brechungsverhältnis (1,658) größer ist als dasjenige des Kanadabalsams (1,53), trifft so schief auf die Kittfläche, daß er nicht in sie einzudringen vermag, sondern an ihr eine vollständige Zurückwerfung nach seitwärts erfährt (s. Brechung, S. 367).
Der außergewöhnliche Strahl dagegen, der sich im Kalkspat rascher fortpflanzt als im Kanadabalsam, durchdringt letztern und verläßt die Hinterfläche als vollkommen polarisierter Strahl d e f, dessen Schwingungen parallel zum Hauptschnitt PHP oder parallel der kürzern Diagonale seiner rautenförmigen Endfläche erfolgen, wie es die Fig. 8 andeutet. Für Strahlen, die senkrecht zu seinem Hauptschnitt schwingen, erscheint das Nicolsche Prisma vollkommen undurchsichtig. Weiteres s. in den Artikeln »Polarisation des Lichtes« und »Zirkularpolarisation«.
Auch die polarisierende Eigenschaft des Turmalins steht mit seiner D. im Zusammenhang. In doppelbrechenden Kristallen ist natürlich nicht nur die Fortpflanzungsgeschwindigkeit, sondern auch die Absorption der Schwingungen abhängig von dem Winkel, den diese mit der optischen Achse bilden, so daß die zur Achse senkrecht schwingenden Strahlen eine andre Absorption erleiden und daher anders gefärbt erscheinen als die parallel zur Achse schwingenden. Diese Eigenschaft (Zweifarbigkeit, Dichroismus) tritt bei manchen Kristallen so auffallend hervor, daß man sie ohne weitere Hilfsmittel beim bloßen Anblick des Kristalls wahrnimmt; der Pennin z. B. erscheint, in der Richtung seiner Achse betrachtet, dunkel blaugrün, senkrecht dazu braun; der Cordierit (Dichroit) ist in der Richtung der Achse dunkelblau, senkrecht zu ihr dagegen gelblichgrau. Der Turmalin ist nun ebenfalls ein »dichroitischer« Kristall, in dem die zur Achse senkrechten Schwingungen des gewöhnlichen Strahles durch Absorption fast vollständig ausgelöscht und nur die zur Achse parallelen des außergewöhnlichen Strahles durchgelassen werden. In manchen amorphen [124] Körpern, sogar in Flüssigkeiten, kann künstlich D. und Dichroismus hervorgerufen werden durch Zug oder Druck, Spannungen infolge rascher Abkühlung, elektrische und magnetische Kräfte. Die Erscheinung beruht offenbar darauf, daß durch die genannten Kräfte die Moleküle teilweise parallel gerichtet werden, während sie sonst so liegen, daß ihre Wirkungen sich gegenseitig aufheben.
Buchempfehlung
Haller, Albrecht von
Versuch Schweizerischer Gedichte
»Zwar der Weise wählt nicht sein Geschicke; Doch er wendet Elend selbst zum Glücke. Fällt der Himmel, er kann Weise decken, Aber nicht schrecken.« Aus »Die Tugend« von Albrecht von Haller
130 Seiten, 7.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Geschichten aus dem Biedermeier. Neun Erzählungen
Biedermeier - das klingt in heutigen Ohren nach langweiligem Spießertum, nach geschmacklosen rosa Teetässchen in Wohnzimmern, die aussehen wie Puppenstuben und in denen es irgendwie nach »Omma« riecht. Zu Recht. Aber nicht nur. Biedermeier ist auch die Zeit einer zarten Literatur der Flucht ins Idyll, des Rückzuges ins private Glück und der Tugenden. Die Menschen im Europa nach Napoleon hatten die Nase voll von großen neuen Ideen, das aufstrebende Bürgertum forderte und entwickelte eine eigene Kunst und Kultur für sich, die unabhängig von feudaler Großmannssucht bestehen sollte. Dass das gelungen ist, zeigt Michael Holzingers Auswahl von neun Meistererzählungen aus der sogenannten Biedermeierzeit.
- Georg Büchner Lenz
- Karl Gutzkow Wally, die Zweiflerin
- Annette von Droste-Hülshoff Die Judenbuche
- Friedrich Hebbel Matteo
- Jeremias Gotthelf Elsi, die seltsame Magd
- Georg Weerth Fragment eines Romans
- Franz Grillparzer Der arme Spielmann
- Eduard Mörike Mozart auf der Reise nach Prag
- Berthold Auerbach Der Viereckig oder die amerikanische Kiste
434 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum