Klang (Musik)
Die Betrachtung des Ursprunges und der wahren Beschaffenheit des Klanges, erkläret so manchen Punkt in der Musik, und giebt verschiedene so wichtige Folgerungen für die Kenntnis der Harmonie, daß sie hier nicht kann übergangen werden.
Der Klang ist ein anhaltender steter Schall, der von dem bloßen Laut, dadurch unterschieden ist, daß dieser nur einzele abgesezte Schläge hören läßt, wie die Schläge eines Hammers; da der Klang anhaltend ist. Wie sich das Herunterfallen einzeler Tropfen, sie folgen schneller oder langsamer auf einander, zu dem steten Rinnen eines Wasserstrales verhält, so verhält sich der bloße Schall oder Laut, der aus einzelen Gehörtropfen besteht, zu dem Klang, der ein ununterbrochenes Fließen des Schalles ist. Die Naturkündiger sagen uns, daß auch der Klang, ob er gleich uns als anhaltend vorkommt, aus wiederholten einzeln und würklich abgesetzten Schlägen bestehe, die aber so schnell auf einander folgen, daß wir den Zwischenraum der Zeit von einem zum andern nicht mehr empfinden, sondern sie in einen steten Ton zusammen hängen; das Ohr zeiget sich hiebey, wie das Aug in ähnlichem Fall. Wenn man in der Dunkelheit eine glüende Kohle schnell wegwirft, so scheinet uns der Weg den sie nihmt, ein steter feuriger Strich, oder eine glüende Schnur zu seyn, ob wir gleich jeden Augenblick nur einen glüenden Punkt dieser Linie sehen.
Diese Bemerkung über die wahre Beschaffenheit des Schalles ist der Grund zur wissenschaftlichen Betrachtung des Klanges und der Harmonie. Besonders wissen wir daher, worin der Unterschied zwischen hohen und tiefen Tönen bestehe, welches die Gelegenheit giebt, die Töne in Ansehung ihrer Höhe gegen einander zu berechnen. Nämlich –
Je schneller die einzelen Schläge, aus denen der Klang besteht auf einander folgen, je höher scheinet[584] uns der Ton zu seyn. Es läßt sich mathematisch beweisen, daß zwey Töne um das Intervall einer Octave von einander abstehen, wenn die Schläge, des einen noch einmal so geschwind auf einander folgen, als die Schläge des andern; und so kann jedes Intervall durch das Verhältnis der Geschwindigkeit der Schläge in Zahlen ausgedruckt werden.
Man hat auf diese Art gefunden, daß der Tiefste in der Musik noch brauchbare Ton, der noch um zwey Octaven tiefer ist, als das sogenannte große C, in einer Secunde 30 Schläge an das Ohr thut; der höchste brauchbare Ton aber, oder das viergestrichene c, in gleicher Zeit 3760.1 Wenn das erwähnte unterste C. 30 Schläge in einer Secunde thut, so thut seine Octave, 60 Schläge in derselben Zeit. Darum kann man sagen, der Unisonus verhalte sich zur Octave, wie 30 zu 60 oder wie 1 zu 2. Also drukt das Verhältnis 1:2 die Octaven aus; und auf eine ähnliche Art das Verhältniß 2:3. die Quinte; weil von zwey Tönen, deren Intervall eine reine Quinte macht, der tiefere zwey Schläge thut, da der höhere drey macht.
Dadurch wird nun der Ausdruk aller Intervalle durch Zahlen, so wie er durch dieses Werk überall gebraucht worden ist,2 verständlich. Einige Tonlehrer drüken die Verhältnisse durch die Länge der Sayten aus. Beydes kommt auf dieselben Zahlen heraus. Denn es ist erwiesen, daß bey klingenden Sayten die Anzahl der Schläge in dem umgekehrten Verhältnis der Länge der Sayten erfolget;3 (wenn nämlich die Sayten sonst gleich und gleich stark gespannt sind,) so daß eine noch einmal so viel Schläge thut, als eine andere, wenn diese noch einmal so lang ist. Daher kann man die Intervalle auch durch die Länge der Sayten ausdrüken; in welchem Fall dieselben Zahlen nur umgekehrt werden. Also müßte nach dieser Art das Verhältnis der Octave durch 2:1, der Quinte durch 3:2 ausgedrückt werden. Dieses sey von der Höhe und und Tiefe des Klanges gesagt.
Aus der wahren Beschaffenheit des Klanges hat man auch entdeket, woher die Reinigkeit eines Tones entsteht; man hat gefunden, daß der Ton rein ist, dessen Schläge durchaus gleich geschwind sind, und sich durch Punkte vorstellen lassen, die alle gleich weit von einander abstehen ....., da der unreine, unmusikalische Ton aus Schlägen besteht, die unordentlich auf einander folgen, wie Punkte die bald weiter bald enger stünden. Auch hat man gefunden, daß dieses Unreine des Tones, bey Sayten daher kommt, daß die Sayten bisweilen an einigen Stellen diker, oder dünner sind, als an andern.
Noch wichtiger als dieses, ist die Entdekung der wahren Ursache der Annehmlichkeit eines reinen Klanges, auf welche die angezeigte Theorie des Klanges geführt hat. Wir wollen diese wichtige Sache so genau, als möglich ist, entwikeln. Wenn wir, wie in den vorhergehenden Anmerkungen geschehen ist, jeden steten, aus nicht zuunterscheidenden Schlägen bestehenden Schall, einen Klang nennen wollen, so giebt es unangenehme, und zur Musik völlig unbrauchbare Klänge, die mehr schnatternde, oder klappernde, als singende Töne bilden. So ist das Rasseln der Räder an einem sehr schnell gehenden Wagen. Es besteht auch aus einzeln Schlägen, die in einander fliessen; aber es verdienet den Namen des Klanges nicht; ist auch dem Gehör nicht angenehm. Aber jeder Klang einer reinen Sayte, einer reinen Gloke, er falle auf welche Höhe er wolle, wenn er nur nicht ganz über, oder unter unsern Gehörkreis liegt, ist angenehm: dessen wird kein Mensch in Abrede seyn. Da nun beydes, das Rasseln eines Rads, und das Klingen einer reinen Sayte, aus schnell und allenfalls in gleichen Zeitpunkten wiederhohlten, in einander fliessenden einzeln Schlägen besteht, woher kommt es, daß dieser angenehm ist?
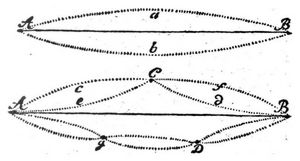
Die Entdekungen, die man über die Beschaffenheit der klingenden Sayten gemacht hat, haben auch die Auflösung dieser Frag an die Hand gegeben oder doch bestätiget. Denn noch ehe man die Bewegungen einer klingenden Sayte zu berechnen wußte, und schon vor der Mitte des vorigen Jahrhunderts, ist die Beobachtung bekannt worden, daß ein reiner etwas tiefer Ton einer Sayte, einem geübten Gehör, außer dem Unisonus, oder Grundton, auch dessen Octave, dessen Duodecime, auch wol gar die zweyte Octave und deren große Terz hören lasse. Eine wichtige Entdekung, wozu aber blos ein feines Gehör erfordert wurd. Um dieses jedem Leser deutlich zu machen, wollen wir also setzen, man schlage eine wol gespannte und reine Sayte an, die den Ton C angebe; wer nun ein feines Gehör hat, vernihmt diesen Ton C so, daß ihn dünkt er höre zugleich, wiewol in geringer Stärke, die [585] Töne c, g, / ē folglich ein Gemenge, oder einen Accord verschiedener und zwar consonirender Töne. Hieraus läßt sich schon begreifen, warum ein solcher Ton voller, mehrklingend und angenehmer ist, als wenn der Ton C ganz allein vernommen würde; jeder Ton ist ein Accord: dadurch hört der Klang auf ein bloßes Klappern zu seyn. Diejenigen, welche die Bewegung, oder die Schwingungen der klingenden Sayte mathematisch untersucht haben, worin der Engländer Taylor zuerst glüklich gewesen ist, haben gefunden, daß eine etwas lange Sayte, wenn sie gestrichen, oder gezupft wird, zwar nach ihrer ganzen Länge schnell hin und her geschwungen wird, (welches Schwingen das Gefühl ihres Tones erwekt) zugleich aber die hälfte, der dritte, der vierte, der fünfte und alle folgende Theile der ganzen Länge der Sayte, jeder für sich noch besondere Schwingungen machen. Einigermaaßen läßt sich dieses mit Augen sehen. An dem Holfeldischen Bogenflügel4 hab ich die besondern Schwingungen der Theile der tiefsten Baßsayten gar ofte und sehr deutlich gesehen. Man stelle sich, um dieses deutlich zu fassen vor, A B sey eine Sayte, deren Ton eine Octave tiefer ist, als unser C.
Indem sie gestrichen wird, und also hin und herschwinget, so daß sie wechselsweise in die Lage A a B und A b B kommt, so theilet sie sich zugleich in mehrere Theile, wie A C, C B, A g, g D, D B u. s. f. und jeder Theil macht für sich wieder besondere Schwingungen, und nihmt die Lagen an, die durch Punkte bezeichnet werden. Dieses ist die wahre Ursache, warum man in einem Klang viel Töne höret. Die Schwingungen der ganzen Sayte erweken das Gefühl ihres Grundtones, den wir nach verhältnismäßiger Zahl seiner Schwingungen 1 nennen wollen. Die Hälfte der Sayte, macht ihre besondere Schwingungen, A c C, A e C, C f B, C d B, in halber Zeit, und erwekt das Gefühl des Tones 2; der dritte, vierte, fünfte, sechste und folgende Theile, der ganzen Sayte machen, jeder wider seine Schwingungen, und erweken das Gefühl der Töne 3, 4, 5, 6 u.s.f. Man stelle sich also viel gleichgespannte und gleichdike Sayten vor, die in Ansehung der Länge sich verhalten, wie folgende Zahlen:
1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9 u.s.f.
so ist, nach der vorhererklärten Bemerkung, der Klang der Sayte 1 aus den Klängen aller übrigen Sayten zusammengesetzt, und ein feines Ohr unterscheidet wenigstens die vier oder fünf ersten, mit ziemlicher Deutlichkeit. In dem Artikel Consonanz sind diese in einem Klang enthaltene Töne, auf dem Notensystem vorgestellt. Merkwürdig ist es, daß diese harmonischen Töne, gerade die sind, welche die Trompete, in der Ordnung, wie sie hier stehen, angiebt, erst den Einklang 1. denn die Octave 1/2, denn die Duodecime 1/3 u.s.f.
Wenn wir nun dieses voraussetzen, so läßt sich begreifen, warum der Klang der Sayten, besonders der Baßsayten, etwas so volles, das Gehör so vergnügendes hat. Denn man hört vieles zugleich, und dieses viele fließt so vollkommen in einander, als wenn es nur eines wäre, und hat also eine schöne Harmonie.
Es läßt sich aus dieser wichtigen Entdekung ungemein viel nützliches für die Musik herleiten, wovon bereits in dem vorhergehenden,5 verschiedenes vorkommt. Ein neuerer französischer Schriftsteller Jamard hat einen nicht ganz mißgerathenen Versuch gemacht, fast gar alle Grundsätze der Harmonie, des Gesangs, und des Takts daraus herzuleiten, welches man mit Vergnügen lesen wird.6 Sein Versuch verdienet weit mehr Beyfall, als der den Rameau, aus der noch unvollkommenen Kenntnis dieser Sache gemacht hat; wovon er und seine meisten Landsmänner, ein gar zu unbescheidenes Rühmen gemacht haben.
Etwas seltsam ist es, daß unser Tonsystem einige der vorhererwähnten harmonischen Töne einzeln ausgeschlossen hat, als den Ton 1/7, 1/11 und andre. Der erwähnte französische Schriftsteller, dringet sehr darauf, daß man sie einführe, und in Deutschland hat vor ihm Hr. Kirnberger angetragen, wenigstens [586] den Ton 1/7, der in unserm System zwischen A und B fallen würde, wie auch Tartini will, anzunehmen.7 Ueber die Bedeutung des Worts Klang, merken wir noch an, daß der Schall, in so fern er anhaltend und wolklingend ist, mit dem Worte Klang, der Klang aber, in so fern er hoch oder tief ist, mit dem Worte Ton bezeichnet wird. Man sagt nie, ein hoher oder tiefer Klang, sondern Ton. In Ansehung der Reinigkeit, sagt man zwar von einer einzelen Sayte, sie habe einen reinen Ton (besser Klang) aber von einem Instrument überhaupt, einer Violin oder einen Clavier, sie habe einen guten Klang.
| 1 | S. Euleri Tentamen Novae theoriae Musicae c. I. §. 13. |
| 2 | Man sehe besondèrs die Art. ⇒ Consonanz; ⇒ Dissonanz; ⇒ Intervall. |
| 3 | S. Art. ⇒ Monochord. |
| 4 | S. ⇒ Fantasien. |
| 5 | Man sehe die Artikel, ⇒ Baß; ⇒ Consonanz; ⇒ Fuge; ⇒ Harmonie u.a.m. |
| 6 | Recherches snrlatheorie de la Musique par Mr. Jamard à Paris et à Rouen 1769. 80. |
| 7 | S. ⇒ System. |
Adelung-1793: Klang, der · Musik, die · Vocal-Musik, die · Trauer-Musik, die · Leichen-Musik, die · Abend-Musik, die · Kammer-Musik, die · Kirchen-Musik, die
Brockhaus-1809: Variationen (Musik) · Russische Horn- oder Jagd-Musik · Die Figural-Musik · Vocal-Musik · Die Jagd- oder Horn-Musik · Die Instrumental-Musik · Horn-Musik · Die Musik
Brockhaus-1911: Türkische Musik · Musik · Griechische Musik
DamenConvLex-1834: Bass (Musik) · Bewegung (Musik) · Bratsche (Musik) · Bariton (Musik) · Arioso (Musik) · Arpeggio (Musik) · Ausdruck in der Musik · Brillante (Musik) · Cantabile (Musik) · Cantate (Musik) · Cantilena (Musik) · Canon (Musik) · Burlesk (Musik) · Cadenz (Musik) · Calando (Musik) · Affabile (Musik) · Affettuoso (Musik) · Agitato (Musik) · Adiaphonon (Musik) · Accelerando (Musik) · Accent (Musik) · Adagio (Musik) · Alla polacca (Musik) · Anschlag (Musik) · Applicatur (Musik) · Aria (Musik) · Animato (Musik) · Alt (Musik) · Amabile (Musik) · Andante (Musik)
Sulzer-1771: Klang (Redende Künste)
Buchempfehlung
Ebner-Eschenbach, Marie von
Der gute Mond / Er laßt die Hand küssen / Ihr Traum. Drei Erzählungen
Drei Erzählungen aus den »Neuen Dorf- und Schloßgeschichten«, die 1886 erschienen.
64 Seiten, 4.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Große Erzählungen der Frühromantik
1799 schreibt Novalis seinen Heinrich von Ofterdingen und schafft mit der blauen Blume, nach der der Jüngling sich sehnt, das Symbol einer der wirkungsmächtigsten Epochen unseres Kulturkreises. Ricarda Huch wird dazu viel später bemerken: »Die blaue Blume ist aber das, was jeder sucht, ohne es selbst zu wissen, nenne man es nun Gott, Ewigkeit oder Liebe.« Diese und fünf weitere große Erzählungen der Frühromantik hat Michael Holzinger für diese Leseausgabe ausgewählt.
- Ludwig Tieck Peter Lebrecht
- Karoline von Günderrode Geschichte eines Braminen
- Novalis Heinrich von Ofterdingen
- Friedrich Schlegel Lucinde
- Jean Paul Des Luftschiffers Giannozzo Seebuch
- Novalis Die Lehrlinge zu Sais
396 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum