Boylesches Gesetz
[244] Boylesches Gesetz. Dasselbe besagt: Bei konstanter Temperatur ist das Volumen eines Gases umgekehrt proportional dem Drucke, dem es ausgesetzt ist. Bezeichnen p, v Druck und Volumen, so soll also stets sein:
pv = Const. = p0v0,
1.
worin Const. für eine bestimmte Gasart nur von der Höhe der konstanten Temperatur abhängt, für verschiedene Gase aber verschieden sein kann (vgl. Boyle-Gay-Lussacsches Gesetz). Der Wert von Const. kann aus Druck und Volumen p0, v0 für irgend einen Zustand bei der fraglichen Temperatur berechnet werden. Bezieht man υ auf die Gewichtseinheit, so läßt sich mit v = 1/γ auch schreiben:
p = γ Const.= γ p0v0,
2.
unter γ das Gewicht der Volumeneinheit Gas verstanden.
Das Boylesche Gesetz wurde 1662 von Robert Boyle mit seinem Schüler Townley entdeckt [1] und 1679 auch durch Edme Mariotte ausgesprochen [2], nach welchem es häufig Mariottesches Gesetz genannt wird. Ueber seine Gültigkeit wurden schon im achtzehnten Jahrhundert und zu Anfang des neunzehnten mehrfach Versuche angestellt. Die zum Teil widersprechenden Resultate derselben veranlaßten anfangs der dreißiger Jahre des letzteren Arago und Dulong, die Frage aufs neue zu prüfen [4]. Sie fanden bei Versuchen mit atmosphärischer Luft von 1–27 Atmosphären Druck und 13° Temperatur, daß die beobachteten Volumen um 1–7‰ kleiner als die aus p0v0 für 1 Atmosphäre nach 1. berechneten waren. Die Abweichungen wurden von ihnen Beobachtungsfehlern zugeschrieben. Da Pouillet für Stickstoff, Sauerstoff, Wasserstoff, Stickoxyd und Kohlenoxyd bis 100 Atmosphären dasselbe Kompressionsgesetz erhielt wie für die zum Vergleich herangezogene atmosphärische Luft [5], so nahm man zunächst die Gültigkeit des Boyleschen Gesetzes für die genannten schwerst kondensierbaren Gase als genügend erwiesen an. Daß Kohlensäure und andre leicht kondensierbare Gase bei Drücken über etwa 4 Atmosphären wesentlich stärkere Volumenänderungen erleiden, als das Gesetz verlangt, hatte Pouillet ebenfalls festgestellt. Für Kohlensäure beispielsweise war bei 40 Atmosphären das beobachtete Volumen nur 0,739 des nach dem Volumen bei 1 Atmosphäre berechneten.
In den vierziger Jahren stellte Regnault Versuche nach wesentlich verbesserter Methode an [6]. Er fand bei etwa 4,4° Temperatur, daß selbst atmosphärische Luft schon für 1 Atmosphäre Druckdifferenz vom Boyleschen Gesetz abweicht. Bei Anfangsdrücken p0 von 1–12 Atmosphären, die nahezu verdoppelt wurden, war
nicht gleich 1, wie Gleichung 1. bestimmt, sondern 1,4–6,4‰ größer. Aehnliche Abweichungen zeigten die übrigen untersuchten Gase, nur für Wasserstoff ergab sich μ<1, wobei die Abweichungen ebenfalls mit dem Drucke wuchsen.
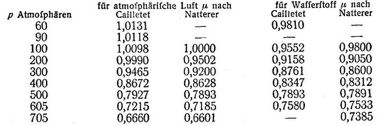
Nach dem bisherigen konnte man schließen, daß die meisten Gase im Gegensatze zu Wasserstoff stärker komprimierbar seien, als das Boylesche Gesetz verlangt, oder mit andern Worten, daß von p0 = 1 Atmosphäre an zu höheren p im allgemeinen die v in wachsendem Maße kleiner, die γ in wachsendem Maße größer würden, als den Gleichungen 1., 2. entspräche. Indessen haben Versuche von Natterer [7], Cailletet [8] und Amagat [9] bei Drücken bis über 3000 Atmosphären ergeben, daß die Abweichungen bei höheren als den früher beobachteten Drücken wieder abnehmen, Null durchschreiten und dann in entgegengesetztem Sinne zunehmen, so daß bei genügend hohen p alle Gase (wie der Wasserstoff schon bei gewöhnlichen Drücken) weniger komprimierbar sind, als das Boylesche Gesetz angibt. Letztere Abweichungen sind weit größer als die zuerst erwähnten. Während nach 2. γ für p = 3000 Atmosphären 3000 mal so groß als für p0 = 1 Atmosphäre sein sollte, erhielt Amagat in diesem Falle bei 15°:
für atmosphärische Luft γ/γ0 = 714
| für Stickstoff | 692 |
| für Sauerstoff | 810 |
| für Wasserstoff | 1037 |
[244] Von unbeschränkter Gültigkeit des Boyleschen Gesetzes kann hiernach keine Rede sein. Da indessen bei gewöhnlicher Temperatur (Cailletet 15°)
wobei angenommen war
| p0 | = | 1 | 100 | 1 | 78 | Atmosphären, |
so kann das Gesetz für atmosphärische Luft und andre schwerst kondensierbare Gase bei gewöhnlicher Temperatur und den gewöhnlich vorkommenden Drücken für die meisten technischen Zwecke als genügend genau gelten. Für Drücke unter 1 Atmosphäre haben die Versuche widersprechende Resultate geliefert, doch sind die betreffenden Abweichungen so klein, daß sie fast immer außer Betracht bleiben können. Während die bisher erwähnten Resultate sich auf gewöhnliche Temperaturen beziehen, haben weitere Versuche von Amagat, Winkelmann u.a. ergeben, daß mit dem Wachsen der Temperatur (solange die chemische Beschaffenheit des Gases ungeändert bleibt) die Abweichungen vom Boyleschen Gesetze abnehmen. So fand Amagat für atmosphärische Luft und Drücke von 1–2 Atmosphären [11]:
| bei t = | 0 | 100 | 150 | 320° |
| μ = | 1,0015 | 1,00011 | 1,00025 | 1,00010. |
Umgekehrt nehmen mit Erniedrigung der Temperatur die Abweichungen zu und in der Nähe der kritischen Temperatur (s.d.) treten Verhältnisse ein, die durch das Boylesche Gesetz auch nicht annähernd wiedergegeben werden können. Vgl. Gase, Dampf, auch gesättigter und überhitzter. Ueber weitere Versuche s. [3], [12], [13], [14].
Literatur: [1] Boyle, New experiments physico-mechanical touching the spring of the air etc., London 1662. – [2] Mariotte, Second essai de physique de la nature de l'air, Paris 1679. – [3] Gehler, Physikalisches Wörterbuch, IV, Leipzig 1828, S. 1026. – [4] Mémoires de l'Académie royale des sciences etc., 1831, X, p. 193. – [5] Pouillet, Élements de physique, 1, 4. édition, Paris 1844, p. 327. – [6] Regnault, Relation des expériences etc., Paris 1847 (zugleich Bd. 21 der Mém. de l'Acad. des sciences), p. 329. – [7] Natterer, Gasverdichtungsversuche, Poggendorfs Annalen, 1855, XCIV, S. 436. – [8] Cailletet, Compressibilite des gaz à hautes pressions, Comptes rendus etc., 1870, LXX, p. 1131. – [9] Amagat, Compressibilite des gaz: oxygene, hydrogène, azote et air jusqu'à 3000 atru., Comptes rendus etc., 1888, CVII, p 522. – [10] Baly und Ramsay, Versuche über die Beziehungen zwischen Druck, Volumen und Temperatur in verdünnten Gasen, Philosophical Magazine etc., 1894, XXXVII, p. 301; vgl. Beiblätter zu Wiedemanns Annalen, 1895, S. 317. – [11] Amagat, Sur la compressibilite de l'air et de l'hydrogène à des températures élevés, Annales de chimie et de physique, 1873, XXVIII, p. 274. – [12] Winkelmann, Handbuch der Physik, I, Breslau 1891, S. 503. – [13] Violle, Lehrbuch der Physik, II, Berlin 1893, S. 809. – [14] Wüllner, Lehrbuch der Experimentalphysik, I, Leipzig 1895, 5. 520. – [15] Zeuner, Technische Thermodynamik, I, Leipzig 1900, S. 91. – [15] Weyrauch, Grundriß der Wärmetheorie, I, Stuttgart 1905, S. 124.
Weyrauch.
Brockhaus-1809: Salisches Gesetz
Brockhaus-1837: Salische Gesetz
Brockhaus-1911: Boylesches Gesetz · Joules Gesetz · Gay-Lussacsches Gesetz · Gesetz · Ohmsches Gesetz · Webersches Gesetz · Salisches Gesetz · Ribuarisches Gesetz · Biot-Savartsches Gesetz · Bernoullisches Gesetz · Avogadros Gesetz · Burgundisches Gesetz · Dulong-Petitsches Gesetz · Daltonsches Gesetz · Coulombs Gesetz
Eisler-1904: Resultanten, Gesetz der psychischen · Relationen, Gesetz der psychischen · Merkelsches Gesetz · Gesetz · Zahl, Gesetz der großen · Webersches Gesetz · Malthusische Gesetz · Gesetz · Fechnersches Gesetz · Excentrischen Empfindung, Gesetz der · Gesetz der drei Stadien · Gesetz der Contraste · Gesetz der bestimmten Anzahl
Goetzinger-1885: Salisches Gesetz
Herder-1854: Salisches Gesetz · Gesetz
Kirchner-Michaelis-1907: psychophysisches Gesetz · Webersches Gesetz · Malthusisches Gesetz · Fechners psycho-physisches Gesetz · Gesetz
Lueger-1904: Dulong-Petitsches Gesetz [1] · Daltons Gesetz · Faradays Gesetz · Dulong-Petitsches Gesetz [2] · Coulombsches Gesetz · Biot-Savartsches Gesetz · Barisches Gesetz · Buys-Ballotsches Gesetz · Boyle-Gay-Lussacsches Gesetz
Buchempfehlung
Schnitzler, Arthur
Frau Beate und ihr Sohn
Beate Heinold lebt seit dem Tode ihres Mannes allein mit ihrem Sohn Hugo in einer Villa am See und versucht, ihn vor möglichen erotischen Abenteuern abzuschirmen. Indes gibt sie selbst dem Werben des jungen Fritz, einem Schulfreund von Hugo, nach und verliert sich zwischen erotischen Wunschvorstellungen, Schuld- und Schamgefühlen.
64 Seiten, 5.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Große Erzählungen der Hochromantik
Zwischen 1804 und 1815 ist Heidelberg das intellektuelle Zentrum einer Bewegung, die sich von dort aus in der Welt verbreitet. Individuelles Erleben von Idylle und Harmonie, die Innerlichkeit der Seele sind die zentralen Themen der Hochromantik als Gegenbewegung zur von der Antike inspirierten Klassik und der vernunftgetriebenen Aufklärung. Acht der ganz großen Erzählungen der Hochromantik hat Michael Holzinger für diese Leseausgabe zusammengestellt.
- Adelbert von Chamisso Adelberts Fabel
- Jean Paul Des Feldpredigers Schmelzle Reise nach Flätz
- Clemens Brentano Aus der Chronika eines fahrenden Schülers
- Friedrich de la Motte Fouqué Undine
- Ludwig Achim von Arnim Isabella von Ägypten
- Adelbert von Chamisso Peter Schlemihls wundersame Geschichte
- E. T. A. Hoffmann Der Sandmann
- E. T. A. Hoffmann Der goldne Topf
390 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum