Schiffsberechnung
[659] Schiffsberechnung umfaßt die Ermittlung der Hauptdimensionen des Schiffsrumpies nach den mit Bezug auf Tragfähigkeit, Geschwindigkeit, größten Tiefgang, Wohnlichkeit, Stabilität und Seefähigkeit gestellten Anforderungen sowie die Berechnung des Deplacements (s.d.), der Spant- und Wasserlinienareale nebst Schwerpunktslagen, der Schwimmlage sowie der Anfangsstabilität.
Die Hauptdimensionen sind: L = Länge des Schiffes, zwischen den Perpendikeln in der Konstruktionswasserlinie (CWL) gemessen; B = größte Breite in der Konstruktionswasserlinie, bei eiserner Außenhaut auf den Spanten, bei hölzerner auf den Planken gemessen; T = mittlerer Konstruktionstiefgang, d.h. die Tiefe in der Mitte der Länge von der Konstruktionswasserlinie bei Eisenschiffen bis Oberkante, Balkenkiel oder Kielplatte, bei Holzschiffen bis Außenkante, Sponung am Kiel gemessen; H = Seitenhöhe in der Mitte der Länge L, bei Eisenschiffen von Oberkante, Balkenkiel oder Kielplatte, bei Holzschiffen von Außenkante, Sponung am Kiel bis Oberkante Hauptdecksbalken, an Bord gemessen. Zur Ermittlung der Hauptdimensionen ist einesteils die Festsetzung des Deplacements, andernteils die Wahl der Verhältniszahlen der Hauptdimensionen sowie der Formkoeffizienten erforderlich.
Das Deplacement des Schiffes setzt sich im allgemeinen aus folgenden Gewichten zusammen: 1. Gewicht des leeren Schiffskörpers; 2. Gewicht der Bemastung, Segel, Tauwerk P/kg; 3. Gewicht von Inventar und Material Q/kg; 4. Gewicht der Besatzung nebst Effekten, Proviant u.s.w. R/kg; 5. Gewicht der Frachtgüter oder der Ladung S/kg; bei Dampfschiffen tritt hinzu: 6. Gewicht der Schiffsmaschine nebst Kessel, Wasser in den Kesseln, Propeller, Hilfsmaschinen und Reserveteile; 7. Gewicht des Kohlenvorrats; bei Passagier- und Auswandererschiffen ferner 8. Gewicht der Passagiere nebst deren Effekten und Proviant; schließlich bei Kriegsschiffen: 9. Gewicht der Geschütze nebst Munition, der Torpedoarmierung sowie der Panzerung. Die Gewichte unter 1.–4. faßt man zusammen als das Eigengewicht (tote Gewicht) des Schiffes; das Gewicht unter 5. heißt Tragfähigkeit oder nützliche Zuladung. Das Eigengewicht bestimmt man meist im Verhältnis zum Deplacement, und dasselbe ist gleich 0,30–0,50 Deplacement, entsprechend der Bauweise und dem Schiffstyp. Bei Kriegsschiffen umfaßt das Schiffskörpergewicht nur die Positionen 1. und 2. Bei Handelsschiffen nimmt man das Eigengewicht zu 120–230 kg mal L B H an. Das Gewicht unter 6. wird im Verhältnis zur indizierten Pferdekraft (IHP) festgesetzt und schwankt zwischen 50 und 200 kg pro 1 IHP, entsprechend der Wahl des Maschinen- und Kesseltyps. Die Zahl der Pferdestärken wird überschläglich nach der französischen Formel angesetzt: IHP = V3 ⊗ : m3 (vgl. Schiffswiderstand), ⊗ = Hauptspantfläche = B T ß, m ein Erfahrungskoeffizient = 3,4–4,0 und V = Geschwindigkeit in Knoten (Seemeilen) pro Stunde. – Der Kohlenvorrat K ergibt sich aus der Formel K = d IHP c : V, worin d der Aktionsradius in Seemeilen, c der Kohlenverbrauch pro indizierte Pferdestärke (0,65–1,0 kg) und V die Schiffsgeschwindigkeit in Knoten (Seemeilen) pro Stunde ist. Die Gewichte zu 5., 8. und 9. ergeben sich aus den gestellten Bedingungen.
Ist das Deplacement nach dem Verwendungszweck des Schiffes festgelegt, so ist es die Aufgabe des Konstrukteurs, für den Linienriß die Hauptdimensionen des Schiffsrumpfes – L, B und T – sowie die Werte der einzelnen Formkoeffizienten – α, ß und δ – so zu, wählen, daß den Anforderungen an Geschwindigkeit, Stabilität, Drehvermögen sowie Festigkeit in günstigster Weise entsprochen wird. Die Länge L als absolute Größe ist abhängig von der vorgeschriebenen Schiffsgeschwindigkeit. Nach Froude ist die Länge des Vorschiffes Lv = 0,1714 V2, die Länge des Hinterschiffes Lh = 0,1144 V2. Das Verhältnis der Schiffslänge zur Schiffsbreite – L : B – ist von Bedeutung für die Bemessung der Stabilität, des Drehvermögens und der Festigkeit der Schiffe. Die Größe von B ist in der Hauptsache durch die Stabilität bedingt und ferner durch die Verhältnisse L : B und T : B festgelegt. Zu großes T : B hat ungenügende Stabilität zur Folge, zu kleines T : B begünstigt bei Segelschiffen das Abtreiben und verursacht bei Schraubenschiffen ungünstige Propellerwirkung.
Die Verhältniszahlen von L : B und T : B sowie die Formkoeffizienten (δ Deplacementskoeffizient, α Wasserlinienkoeffizient und ß Hauptspantkoeffizient), entsprechend den Formeln: Deplacement in cbm = LBT δ; Wasserlinienareal = L B α; Hauptspantareal = B T ß, ergeben sich für die einzelnen Schiffstypen aus der nachfolgenden Tabelle; dabei besteht zwischen den Völligkeitsgraden nach Normand folgende Beziehung: δ = k α β worin k = 0,82 bis 0,90, im Mittel = 0,87 ist.[659]
Setzt man L : B = m, T : B = n, so ergibt sich das Gewichtsdeplacement aus folgender Gleichung:
woraus B und demnach L und T sich bestimmen lassen.
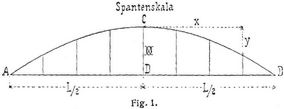
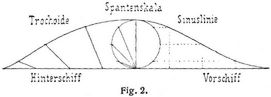
Die Verteilung der Volumdeplacements oder des Auftriebs auf die Länge des Schiffes und dementsprechend der Entwurf des Spantenrisses (s. Stanzen) erfolgt nun mit Hilfe der Deplacementsskala. Trägt man von der Linie A B (Fig. 1) gleich der Länge des Schiffes L Ordinaten auf, deren Längen proportional dem Areal der betreffenden Spanten sind, so ist die durch die Endpunkte der Ordinaten gezogene Kurve die Deplacementsskala oder Spantenskala, und die von der Linie A B und der Kurve eingeschlossene Fläche gibt alsdann die Größe des Deplacements in Kubikmetern an. Konstruiert man die Deplacementsskala nach der Parabel, so wird, wenn C D dem Hauptspantareal gleichgemacht wird, y = ⊗ [x : 0,5 L]m, wobei m = Deplacement: (⊗ L – Deplacement) = δ : (ß – δ) ist. Für scharfe Schiffe ergeben sich nach Colin Archer günstige Schiffsformen, wenn die Deplacementsskala im Vorschiff nach der Sinuslinie, im Hinterschiff nach einer Trochoide konstruiert wird (Fig. 2). Nach den Spantordinaten der Deplacementsskala werden nun die Spantkurven entsprechend den Spantarealen gezeichnet und letztere sowie deren Schwerpunktslage nach der Simpsonschen Regel oder mit Hilfe des Planimeters berechnet. Der Schwerpunkt der von der Spantenskala abgeschlossenen Fläche stimmt mit dem Schwerpunkt des Deplacements der Länge nach überein.
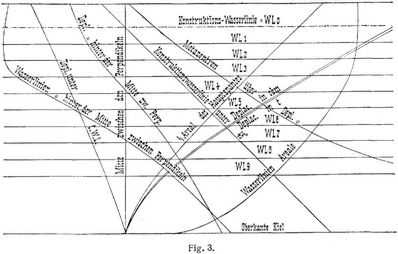
Konstruiert man in gleicher Weise eine Deplacementsskala mit Bezug auf die als Koordinatenachse gedachte Senkrechte durch die Mitte der Länge zwischen den Perpendikeln und das Wasserlinienareal der Konstruktionswasserlinie als Endabszisse (Fig. 3), so ergeben die dazwischen liegenden Abszissen die Areale der Wasserlinien für die entsprechenden Tiefgangslagen an. Man nennt diese Deplacementsskala die Wasserlinienskala. Die Areale und Schwerpunktslagen der einzelnen Wasserlinien werden gleichfalls nach der Simpsonschen Regel berechnet. Der Schwerpunkt der von der Wasserlinienskala begrenzten Fläche fällt mit dem Deplacementsschwerpunkt der Höhe nach überein. Die Berechnung des Volumendeplacements kann daher sowohl nach den Spantarealen – Spantenskala – als auch nach den Wasserlinienarealen – Wasserlinienskala – erfolgen, und man führt meist beide Rechnungen durch, um durch Uebereinstimmung der Resultate eine Kontrolle zu haben. Der Lastenmaßstab stellt eine Kurve dar, bei welcher die Ordinaten die Tiefgänge, entsprechend den einzelnen Wasserlinien, darstellen, während die Abszissen die Größe des Deplacements für die entsprechenden Tiefgänge in[660] Kubikmetern wiedergeben, so daß man für eine bestimmte Größe des mittleren Tiefgangs die entsprechende Größe des Deplacements in Kubikmetern ablesen kann. Zum Ablesen des Deplacements in Tonnen (für Seewasser 1 cbm = 1,015 t) wird meist eine zweite Kurve gezeichnet, die ähnlich der ersteren verläuft und dann die Lastigkeit des Schiffes für einen mittleren Tiefgang angibt; umgekehrt kann man bei Hinzufügung oder Wegnahme von Gewichten den entsprechenden Tiefgang abgreifen.
Die Spantinhaltsskalen, meist Integralkurven genannt (Fig. 4), geben für die einzelnen Tiefgänge als Ordinate die entsprechenden Spantinhalte, vom Nullpunkt an gerechnet. Sie werden in der Hauptsache benutzt zur Berechnung des Deplacements bei von der Konstruktionslage abweichender Schwimmlage des Schiffes sowie zur Trimmberechnung, falls eine oder mehrere Abteilungen durch ein Leck überflutet sind.
Zur Bestimmung der Formstabilität um die Längsachse ist die Entfernung des Metazentrums M (s.d.) vom Deplacementsschwerpunkt F zu berechnen nach
Nach der Simpsonschen Regel ist demnach:
worin y0 bis yn die Ordinaten der oberen Wasserlinien und ∆ x deren Abstand voneinander ist.
Die Höhe des Longitudinalmetazentrums über dem Deplacementsschwerpunkt bei Neigungen des Schiffes um die Querachse ergibt sich aus
worin y1 und y2 Ordinaten bedeuten, die parallel zur Längsachse des Schiffes von einer durch den Schwerpunkt der Wasserlinienfläche gelegten Querachse aus gezogen sind. Um für die Berechnung des Longitudinalmetazentrums die gewöhnlichen Spantordinaten benutzen zu können, dient folgende Umformung:
worin k die Entfernung des Schwerpunkts der oberen Wasserlinie von der ersten Ordinate bezeichnet und
den Flächeninhalt der oberen Wasserlinienfläche Das Integral
wird wie folgt nach der Simpsonschen Regel berechnet:
Die Größe des Longitudinalmetazentrums wird für die Trimmberechnung des Schiffes, d.h. die genaue Ermittlung der Schwimmlage eines Schiffes bei Verschiebungen von Gewichten längsschiffs, benutzt. Die Ergebnisse der Berechnungen werden meistens in einem Schaubild vereinigt (Fig. 3). Alle Größen werden auf den einzelnen Wasserlinien von der Senkrechten durch die Mitte zwischen den Perpendikeln abgetragen, mit Ausnahme der Werte für die metazentrischen Höhen M F und M F1, welche von der Kurve der Deplacementsschwerpunkte der Höhe nach abgetragen werden; für die Werte von M1 F wählt man einen kleineren Maßstab.
Zur annähernden Bestimmung der Entfernung des Deplacementsschwerpunkts unter der Konstruktionswasserlinie, der Größe des Quer- und Längenmetazentrums über dem Deplacementsschwerpunkt sowie der benetzten Oberfläche hat Normand Annäherungsformeln aufgestellt, die im allgemeinen gute Werte ergeben [1], [5].
Literatur. [1] Krieger, Johows Hilfsbuch für den Schiffbau, Berlin 1902. – [2] »Hütte«, Ingenieurtaschenbuch, Berlin 1908. – [3] Neudeck, Leitfaden für den Unterricht im Schiffbau, Berlin 1902. – [4] Pollard & Dudebout, Theorie du navire, Paris 1894. – [5] Normand, Formules approximatives de construction navale, Paris 1897. – [6] Herner, H., Die Theorie des Schiffes, Hannover 1908.
T. Schwarz.
Buchempfehlung
Droste-Hülshoff, Annette von
Gedichte (Die Ausgabe von 1844)
Nach einem schmalen Band, den die Droste 1838 mit mäßigem Erfolg herausgab, erscheint 1844 bei Cotta ihre zweite und weit bedeutendere Lyrikausgabe. Die Ausgabe enthält ihre Heidebilder mit dem berühmten »Knaben im Moor«, die Balladen, darunter »Die Vergeltung« und neben vielen anderen die Gedichte »Am Turme« und »Das Spiegelbild«. Von dem Honorar für diese Ausgabe erwarb die Autorin ein idyllisches Weinbergshaus in Meersburg am Bodensee, wo sie vier Jahre später verstarb.
220 Seiten, 11.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Große Erzählungen der Hochromantik
Zwischen 1804 und 1815 ist Heidelberg das intellektuelle Zentrum einer Bewegung, die sich von dort aus in der Welt verbreitet. Individuelles Erleben von Idylle und Harmonie, die Innerlichkeit der Seele sind die zentralen Themen der Hochromantik als Gegenbewegung zur von der Antike inspirierten Klassik und der vernunftgetriebenen Aufklärung. Acht der ganz großen Erzählungen der Hochromantik hat Michael Holzinger für diese Leseausgabe zusammengestellt.
- Adelbert von Chamisso Adelberts Fabel
- Jean Paul Des Feldpredigers Schmelzle Reise nach Flätz
- Clemens Brentano Aus der Chronika eines fahrenden Schülers
- Friedrich de la Motte Fouqué Undine
- Ludwig Achim von Arnim Isabella von Ägypten
- Adelbert von Chamisso Peter Schlemihls wundersame Geschichte
- E. T. A. Hoffmann Der Sandmann
- E. T. A. Hoffmann Der goldne Topf
390 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum