Wechselstrom, elektrischer
[887] Wechselstrom, elektrischer, Strom von wechselnder Größe und Richtung.
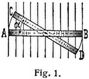
Rechnet man die Drehung eines kreisförmigen Drahtringes in einem homogenen, magnetischen Felde von der Lage aus, in welcher er das Maximum N0 der Kraftlinien einschließt, so beträgt die Zahl der eingeschlossenen Kraftlinien in der um den Winkel α gedrehten Lage (Fig. 1) N = N0 cos α. Nun folgt aber der Momentanwert der elektromotorischen Kraft zur Zeit t in Volt (Bd. 5, S. 184) e = – d N/d t ξ 10-8, so daß in unserm Falle wird:
unter ξ die Windungszahl des Drahtringes und d α : d t = ω die Winkelgeschwindigkeit der Rotation verbanden.
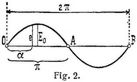
Fig. 2 zeigt den Verlauf der Veränderlichkeit von e mit α als Abszisse und e als Ordinate (Sinuslinie). Man erkennt, daß für α = 90°, d.h. während der ersten Viertelumdrehung e bis zu seinem Maximum E0 = N0 ξ ω · 10-8 wächst, dann wieder abnimmt, um nach einer halben Umdrehung den Wert Null anzunehmen, dann wieder, jedoch mit umgekehrten Vorzeichen, wächst bis zu dem negativen Maximum E0, dann abermals bis Null abnimmt u.s.f. Nach jeder ganzen Umdrehung (Oszillation) des Ringes wiederholt sich der Vorgang; eine Oszillation entspricht also einer Periode des Wechselstromes von bestimmter Zeitdauer T. Frequenz ist die Zahl der Perioden pro Sekunde.
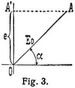
Man erhält aus 1. mit Einsetzen des vorhin gefundenen Wertes E0 die Gleichung e = E0 · sin α, bezw. da bei konstantem ω die Gleichung d α : d t = ω integriert werden kann: e = E0 · sin α = E0 · sin (ω t). Die Gleichung α = ω t gilt für jeden Wert von t, also auch für den Wert t = T der Zeitdauer einer Periode. Diese ist vollendet für α = 2π, also ist 2π = ω T und hiermit ω = 2π : T. Ist ~ die Anzahl der Perioden in einer Sekunde, so ist T = 1/~ und demnach ω = 2π ~. Anstatt e als die Ordinaten der Sinuslinie darzustellen, kann man auch[887] unter dem Winkel α gegen eine als Abszissenachse angenommene Gerade eine Strecke O A (Fig. 3) gleich dem Maximalwert E0 abtragen und diese auf eine zur Abszissenachse senkrechte Gerade projizieren; die Projektion O A' ist alsdann der momentane Wert e (Vektordiagramm).
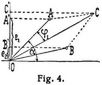
Denkt man sich nun zwei genau gleiche Drahtringe auf die Rotationsachse gesetzt, deren Ebenen einen Winkel φ0 miteinander einschließen, so unterscheiden sich die in den beiden Drahtringen erzeugten elektromotorischen Kräfte nur dadurch, daß die Momentanwerte in dem zweiten Drahtringe die gleichen des ersten um den Winkel φ0 später erreichen. Wenn also die elektromotorische Kraft des ersten Ringes durch die Gleichung e1 = E0 · sin α gegeben ist, so ist die des zweiten bestimmt durch die Gleichung e2 = E0 sin (α – φ0). Man kann nun die beiden Wechselströme so verbinden, daß sich die elektromotorischen Kräfte entweder in jedem Augenblicke addieren oder subtrahieren. Beim Addieren herrscht also in einem bestimmten Augenblick an den Drahtenden die Gesamtspannung e = E0 sin α + E0 sin (α – φ0), welcher Ausdruck sich umformen läßt in e = E sin (α – φ1), so daß also die Gesamtspannung ebenfalls sinusförmigen Verlauf besitzt, deren Maximalwert E ist, und die in der Phase gegen die elektromotorische Kraft der ersten Maschine um den Winkel φ1 zurückbleibt. Besser übersieht man das Resultat, wenn man die einzelnen Momentanwerte im Vektordiagramm sichtbar macht. In Fig. 4 sei O A der Maximalwert der elektromotorischen Kraft des ersten Drahtringes, O B diejenige des zweiten; dann ist O A' der Momentanwert e1 und O B' der Momentanwert e2. Die Summe e1 + e2 sei dargestellt O C', und man ersteht sofort, daß diese Summe die Projektion der Diagonale O C des # O A C B ist.
Fließt ein Wechselstrom, dessen Momentanwert i ist, durch einen induktionsfreien Widerstand w, so ruft er an den Enden des Widerstandes einen Spannungsunterschied hervor; ist dessen Momentanwert e, dann ergibt sich i = e : w. Wird der Wechselstrom von der oben betrachteten Wechselstrommaschine hervorgebracht, so ist e = E0 sin α, und es wird auch i = E0 sin α : w = J0 sin α, wo J0 = E0 : w gesetzt wurde. Stellt man die Momentanwerte i und e durch die Projektionen ihrer Vektoren dar, so sieht man, daß die Vektoren E0 und J0 sich nur durch die Größe und den gewählten Maßstab, hingegen nicht durch die Richtung unterscheiden, so daß wir sagen können: Im induktionsfreien Widerstande fällt der Vektor des Stromes mit dem Vektor der Spannung zusammen.
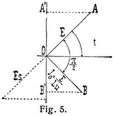
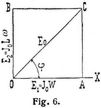
Der Wechselstrom möge durch eine widerstandslos gedachte Spule ohne Eisenkern fließen, deren Selbstinduktionskoeffizient L sei. Fließt ein Wechselstrom i durch eine derartige Spule, so ruft dieser, da er ja von Kraftlinien begleitet ist, eine elektromotorische Kraft der Selbstinduktion hervor, deren Größe durch die Formel es = – L d i/d t (Bd. 5, S. 185) gegeben ist, und die der Klemmenspannung ek der Spule entgegenwirkt. Bezeichnet zunächst w den Widerstand der Spule, so ist i = (ek + es) : w der Strom, der durch die Spule fließt. Hieraus folgt i w = ek + es, und wenn w = 0 ist, ek = – es. Die Klemmenspannung ek rührt von unsrer Wechselstrommaschine her, ändert sich also nach der Gleichung ek = E sin (ω t), während es = –L d i/d t ist; also gilt die Gleichung E sin (ω t) = + L d i/d t, woraus durch Integration i = –E/(L ω) cos(ω t) folgt. Der Nenner L ω stellt einen Widerstand vor, der Induktanz genannt wird. Stellt man die Momentanwerte ek, i, es durch Projektionen im Vektordiagramm dar, so zeigt Fig. 5 die Resultate, welche in Worte gekleidet folgende sind: Durchfließt ein Wechselstrom von sinusförmigem Verlauf eine widerstandslose Induktionsspule, so steht im Vektordiagramm der Vektor der Stromstärke (O B) senkrecht auf dem Vektor der Klemmenspannung O A, und zwar im Sinne des Zurückbleibens. Der Klemmenspannung genau entgegengerichtet ist die elektromotorische Kraft der Selbstinduktion, so daß diese hinter dem Strome um 90° zurückbleibt. Eine Spule, die Widerstand und Selbstinduktion besitzt, kann als die Hintereinanderschaltung eines induktionsfreien Widerstandes W und einer widerstandslosen Spule mit dem Selbstinduktionskoeffizienten L angesehen werden. Wird diese an eine Wechselstromquelle angeschlossen, so fließt durch sie ein Strom, dessen Richtung im Vektordiagramm durch die Linie O X (Fig. 6) dargestellt sein möge. Dieser erzeugt an den Enden des induktionsfreien Widerstandes eine Klemmenspannung, deren Maximalwert E1 = J0 W ist und welche in der Richtung von O X fällt (0 A = E1 = J0 W). An den Klemmen der widerstandslosen Induktionsspule herrscht eine Spannung E2 = J0 L ω, welche dem Strom um 90° vorauseilt (O B = E2 = J0 L ω). Die Resultierende E0 aus O A und O B gibt dann die Gesamtspannung an, welche die Maschine zu erzeugen hat. Man steht hieraus, daß die Gesamtspannung um einen Winkel φ, »den Phasenverschiebungswinkel«, der Richtung des Stromes vorauseilt, d.h. denkt man sich das Quadrat A O B C im entgegengesetzten Sinne des Uhrzeigers um O rotierend, und die Projektionen der Gesamtspannung und des Stromes auf eine vertikale Gerade gebildet, so sieht man, daß der Strom immer um den Winkel φ später die Maximal- und Nullwerte als die Spannung erreicht. Der Maximalwert J0 des Stromes kann aus dem rechtwinkligen Dreieck A O C berechnet werden, denn es ist O C2 = (J0 W)2 + (J0 ω L.)2, woraus
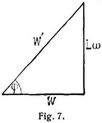
folgt. Den Nenner dieses[888] Ausdrucks nennt man den scheinbaren Widerstand oder die Impedanz. Man kann ihn als die Hypotenuse eines rechtwinkligen Dreiecks darstellen, dessen eine Kathete der wahre Widerstand W und dessen andre die Induktanz L ω ist (Fig. 7). Der scheinbare Widerstand und mit ihm die Phasenverschiebung wird um so größer, je größer die Periodenzahl des Wechselstromes ist. Da beide Erscheinungen jedoch unwillkommene sind, darf man die Periodenzahl nicht zu hoch wählen. Bogenlampen brauchen Ströme von mindestens 40 Perioden, wenn man nicht ein Zittern des Lichtes bemerken soll. Die Werke für Licht und Kraft erzeugen daher meistens Ströme von 50 oder 42 Perioden. Für reine Kraftwerke werden 25 bis herab zu 13 Perioden gewählt. Wechselströme mit sehr wesentlich höheren Frequenzen wurden mit Maschinen zuerst von Tesla erzeugt und untersucht (Teslaströme s. unten).
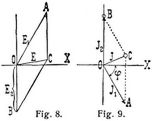
Während, wie gezeigt, bei einem Induktionswiderstand der Vektor des Stromes zurückbleibt gegen den Vektor der Spannung, eilt bei einem in den Wechselstromkreis eingeschalteten Kondensator der Strom, dessen Stärke i' = c e' ω ist, um 90° der Spannung voraus. Die Stromstärke nimmt mit der Periodenzahl zu, während sie in einer Spule kleiner wird. Für Gleichstrom ist ein Kondensator ein Isolator, für Wechselströme hoher Periodenzahl dagegen ein guter Leiter. Ist ein Induktionswiderstand und ein Kondensator hintereinander in einen Wechselstrom eingeschaltet, so entstehen an den Klemmen des Induktionswiderstandes und des Kondensators Spannungen, deren Maximalwerte E1 und E2 seien. Ist (Fig. 8) O X die Richtung des Stromvektors, so ist O A = E1 die Richtung des Vektors der Klemmenspannung am Induktionswiderstande und O B = E2 die Klemmenspannung des Kondensators. Die Gesamtspannung, die von der Stromquelle herrührt, ist die Diagonale O C. Wie die Figur zeigt, ist diese kleiner als E1, sie kann aber auch kleiner als E2 sein. Die Phasenverschiebung ist durch den Winkel C O X dargestellt. Ist derselbe Null, so gilt die Gleichung L ω = 1 : c' ω, wo C die Kapazität des Kondensators bezeichnet. Da ein Kabel die Eigenschaften eines Kondensators besitzt, so zeigen sich die genannten Erscheinungen auch an langen Kabeln (Ferranti-Effekt). Schaltet man einen Kondensator parallel zu einem Induktionswiderstande, so gibt Fig. 9 die eintretenden Verhältnisse an. Es sei O X die Richtung der gemeinsamen Spannung, O A = J1 der Strom im Induktionswiderstande, welcher gegen die Spannung um den Phasenverschiebungswinkel φ zurückbleibt, O B = J2 der Strom im Kondensator, welcher der Spannung um 90° vorauseilt, dann gibt die Resultierende O C den Gesamtstrom in der Zuleitung an. Man erkennt, daß der Gesamtstrom kleiner sein kann als jede der Komponenten, und macht Gebrauch von dieser Kondensatoreigenschaft, indem man dem Swinburneschen Igeltransformator einen Kondensator parallel schaltete, und so den Strom in der Zuleitung wesentlich verringert.
Enthält eine Spule Eisenkerne, so wird die Stromkurve von der Sinuslinie stark abweichen, und infolge dessen verlieren die obigen Formeln zum Teil ihre Gültigkeit. Man zerlegt dann den Strom in zwei Komponenten: die Nutzkomponente, welche mit der Richtung der Spannung zusammenfällt, und die wattlose Komponente, welche senkrecht auf der Spannungsrichtung steht. Die erstere deckt die Verluste durch Stromwärme, Hysteresis und Wirbelströme und ist definiert durch die Gleichung: Spannung mal Nutzkomponente gleich Effektverlusten; die letztere (i' μ) dient zur Erzeugung der Kraftlinien. Sie folgt aus der Gleichung: N0 = (0,4 π i μ ξ √2) : w, worin N0 die maximale Kraftlinienzahl, ξ die Windungszahl und w den magnetischen Widerstand des Kreises bedeutet. Die Gleichung läßt sich umformen in die für Anwendungen bequemere Σ H l = 0,4 π ξ i' μ √2, wo l die Weglänge der Kraftlinie in der Induktion B bezeichnet und zu der die aus einer Magnetisierungskurve zu entnehmende magnetisierende Kraft H gehört. Das Kraftlinienfeld N0 erzeugt in den Windungen eine elektromotorische Gegenkraft e's, deren Größe durch die Gleichung e's = 4,44N0 ξ ~ 10-8 gegeben ist. Die angegebenen Gleichungen finden Verwendung bei der Berechnung von Drosselspulen (s. Umformer, elektrischer), die entweder einer Bogenlampe vorgeschaltet oder zu hintereinander geschalteten Glühlampen parallel geschaltet werden. Zum Messen von Wechselströmen braucht man Instrumente, bei denen der Ausschlag von dem Quadrate der Stromstärke abhängt, weil nur bei diesen der Ausschlag unabhängig von der Stromrichtung ist. Solche Instrumente sind die Elektrodynamometer und die Hitzdrahtvoltmeter (s. Meßinstrumente, elektrotechnische, Bd. 6, S. 378 u. 379).
Bei dem Elektrodynamometer ist der Ausschlag proportional dem Mittelwerte aus dem Quadrate der Stromstärke, so daß die gemessene Stromstärke definiert ist durch die Gleichung i'2 = Σ i2 : m, wo Σ i2 die Summe der momentanen Werte und m die Anzahl der Addenden dieser Summe vorstellt. Man nennt i' die effektive Stromstärke.
Mit dem Hitzdrahtvoltmeter mißt man die effektive Spannung e'. Die Beziehung, die zwischen dem größten der Momentanwerte, »dem Maximalwert«, und dem effektiven Wert herrscht, richtet sich nach der Gestalt der Kurve in Fig. 2. Ist diese eine Sinuslinie, so wird e' = E0 : √2, worin E0 den Maximalwert bezeichnet. In gleicher Weise gilt i' = J0 : √2, also ist auch
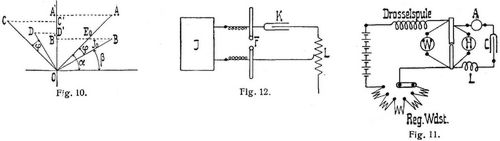
Das Produkt e i aus den Momentanwerten von Spannung und Strom Stellt den momentanen Effekt vor, d.h. die Arbeit, welche der Strom in einer Sekunde leisten würde, wenn von dem betrachteten Augenblick an Spannung und Strom konstant würden; der wahre Effekt E ist der Mittelwert aus den Momentaneffekten, also E = Σ e i : m, wo m die Anzahl der Addenden bezeichnet. Um den Effekt zu bestimmen, der in einer Induktionsspule geleistet wird, stelle man sich die Momentanwerte im Vektordiagramm (Fig. 10) für zwei um 90°[889] verschiedene Stellungen dar. Es ist für die erste Lage O A' = e1 = E0 sin α, O B' = i1 = J0 sin β, also e1 i1 = E0 J0 sin α · sin β. Für die zweite Lage, von der erden um 90° entfernt, ist O C' = e2 = E0 sin (α + 90°) = E0 cos α; O D' = i2 = J0 sin (β + 90°) = J0 cos β; also e2 i2 = E0 cos α · J0 cos β; hieraus: e1 i1 + e2 i2 = E0 J0 (sin α sin β + cos α cos β) = E0 J0 · cos (α – β) = E0 J0 · cos φ. Man erhält also: Σ e i = m/2 · E0 J0 cos φ, demnach G = 1/2 E0 J0 cos φ = E0/√2 · J0/√2 cos φ = e' i' cos φ, d.h. der Effekt eines Wechselstromes wird gefunden, indem man die gemessene Spannung und die gemessene Stromstärke mit dem Cosinus des Phasenverschiebungswinkels (Leistungsfaktor) multipliziert. Die Formel gibt jedoch nur dann richtige Resultate, wenn der Wechselstrom, wie bisher vorausgesetzt, einen der Sinuslinie entsprechenden Verlauf hat. Zur Messung eines Wechselstromeffektes reichen das Amperemeter und Voltmeter nicht aus, da man den Phasenverschiebungswinkel nicht kennt. Ein allen prakischen Anforderungen genügendes Instrument ist jedoch das Wattmeter (vgl. Meßinstrumente, elektrotechnische, Bd. 6, S. 371). Ist kein Wattmeter vorhanden, so kann man sich auch der Methode der drei Amperemeter oder der Methode der drei Voltmeter bedienen. Wechselströme mit sehr hoher Periodenzahl, die vor allem durch den großen, scheinbaren Widerstand ihrer Leiter auffallen und bei denen selbst kleine Kondensatoren schon wesentliche Ströme leiten, können ohne Maschinen noch auf folgende Weise erzeugt werden: Von einer Gleichstromquelle, die 65 Volt bis einige 100 Volt haben kann, fließt durch eine Drosselspule (Fig. 11), einen Regulationswiderstand und ein paar Homogenkohlen ein Gleichstrom von etwa 3–6 Ampère. Parallel zu den Kohlen ist ein Kondensator mit der Kapazität C und eine Spule L mit wenig Windungen angeschlossen. Es gelingt leicht, den Lichtbogen durch passende (kleine) Entfernung der Kohlen zu einem pfeifenden Ton zu veranlassen, in welchem Falle dann durch den Kondensator ein kräftiger Wechselstrom fließt, der durch das Hitzdrahtampèremeter A gemessen werden kann. Die Tonhöhe und somit die Periodenzahl des Wechselstromes ändert sich entsprechend der Gleichung L ω = 1 : C ω oder ω = 1 : √(C L). Man hat hiermit die Möglichkeit, durch Aenderung der Größen C und L Wechselströme von nahezu beliebig hoher Periodenzahl zu erzeugen.
Auch durch die Entladung von Leidener Flaschen können, wie schon Feddersen nachgewiesen hat, oszillatorische Ströme entstehen. In Fig. 12 bedeute J einen Funkeninduktor, F eine sogenannte Funkenstrecke, d.h. zwei blanke Zinkkugeln, die einander auf einige Millimeter genähert werden können, K eine Leidener Flasche und L eine aus wenigen Windungen blanken Drahtes bestehende regulierbare Selbstinduktion. Bei jeder Unterbrechung des Induktors entsteht dann in dem Stromkreise F K L ein Wechselstrom von sehr hoher Periodenzahl.
Literatur: Kapp, G., Dynamomaschinen für Gleich- und Wechselstrom, Berlin 1904; Arnold, Die Wechselstromtechnik, Karlsruhe 1904; Holzt, Die Schule des Elektrotechnikers, Leipzig 1910.
Holzt.
Brockhaus-1911: Wechselstrom · Elektrischer Strom · Elektrischer Ofen · Elektrischer Wagen · Elektrischer Verbrauchsmesser · Elektrischer Effekt · Elektrischer Akkumulator · Elektrischer Funke · Elektrischer Motor · Elektrischer Generator
Herder-1854: Elektrischer Funke
Lueger-1904: Umformer, elektrischer · Elektrischer Wecker · Elektrischer Pflug
Meyers-1905: Elektrischer Scheinwerfer · Elektrischer Strom · Elektrischer Widerstand · Elektrischer Pflug · Elektrischer Rückstand · Elektrischer Schatten · Elektrischer Wind · Schlüssel, elektrischer · Strahlen elektrischer Kraft · Strom, elektrischer · Rückstand, elektrischer · Schatten, elektrischer · Schlittenapparat, elektrischer · Elektrischer Antrieb · Elektrischer Auszug · Elektrischer Doppelschatten · Ausstrahlung elektrischer Wellen · Bogen, elektrischer · Effekt, elektrischer · Elektrischer Effekt · Elektrischer Kurzschluß · Elektrischer Omnibus · Elektrischer Oszillātor · Elektrischer Funke · Elektrischer Geruch · Elektrischer Korkkugeltanz
Pierer-1857: Elektrischer Schörl · Elektrischer Strom · Elektrischer Telegraph · Elektrischer Aal · Elektrischer Auslader · Elektrischer Funke
Buchempfehlung
Jean Paul
Titan
Bereits 1792 beginnt Jean Paul die Arbeit an dem von ihm selbst als seinen »Kardinalroman« gesehenen »Titan« bis dieser schließlich 1800-1803 in vier Bänden erscheint und in strenger Anordnung den Werdegang des jungen Helden Albano de Cesara erzählt. Dabei prangert Jean Paul die Zuchtlosigkeit seiner Zeit an, wendet sich gegen Idealismus, Ästhetizismus und Pietismus gleichermaßen und fordert mit seinen Helden die Ausbildung »vielkräftiger«, statt »einkräftiger« Individuen.
546 Seiten, 18.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Romantische Geschichten II. Zehn Erzählungen
Romantik! Das ist auch – aber eben nicht nur – eine Epoche. Wenn wir heute etwas romantisch finden oder nennen, schwingt darin die Sehnsucht und die Leidenschaft der jungen Autoren, die seit dem Ausklang des 18. Jahrhundert ihre Gefühlswelt gegen die von der Aufklärung geforderte Vernunft verteidigt haben. So sind vor 200 Jahren wundervolle Erzählungen entstanden. Sie handeln von der Suche nach einer verlorengegangenen Welt des Wunderbaren, sind melancholisch oder mythisch oder märchenhaft, jedenfalls aber romantisch - damals wie heute. Michael Holzinger hat für den zweiten Band eine weitere Sammlung von zehn romantischen Meistererzählungen zusammengestellt.
- Novalis Die Lehrlinge zu Sais
- Adelbert von Chamisso Adelberts Fabel
- Jean Paul Des Feldpredigers Schmelzle Reise nach Flätz
- Clemens Brentano Aus der Chronika eines fahrenden Schülers
- Friedrich de la Motte Fouqué Eine Geschichte vom Galgenmännlein
- E. T. A. Hoffmann Der goldne Topf
- Joseph von Eichendorff Das Marmorbild
- Ludwig Achim von Arnim Die Majoratsherren
- Ludwig Tieck Die Gemälde
- Wilhelm Hauff Die Bettlerin vom Pont des Arts
428 Seiten, 16.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum