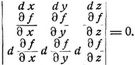Flächentheorie
[72] Flächentheorie. Fläche (Oberfläche) ist eine zweifach ausgedehnte Raumgröße, die Begrenzung eines Körpers. Sie ist entweder eben (Ebene) oder krumm (eigentliche Fläche). Sie besitzt eine Gleichung zwischen drei Veränderlichen f (x, y, z) = 0 und heißt je nach der Natur der Funktion f algebraisch oder transzendent. An Stelle der Gleichung kann auch die Parameterdarstellung treten: x = φ (u, v); y = ψ (u, v); z = χ (u, v). Flächen mit unendlich vielen Geraden heißen Regelflächen; dieselben werden abwickelbar genannt, wenn je zwei benachbarte Flächengeraden sich schneiden, andernfalls windschief.
A. Allgemeine Eigenschaften der algebraischen Flächen. Der Grad n der Gleichung f (x, y, z) = 0 heißt Ordnung der Fläche; er ist die Zahl ihrer Schnittpunkte mit einer beliebigen Geraden. Eine beliebige Ebene schneidet die Fläche in einer Kurve nter Ordnung. Zwei Flächen von den Ordnungen m und n haben eine Raumkurve m · nter Ordnung gemein; drei Flächen von den Ordnungen m, n und p schneiden sich in m · n · p Punkten. Eine Fläche n-ter Ordnung ist durch n (n2 + 6 n + 11)/6 Punkte bestimmt. In jedem Flächenpunkt (ξ, η, ζ) existieren unendlich viele Tangenten, die sämtlich in der Tangentialebene (ξ – x) ∂f/∂ξ + (η – y) ∂f/∂η + (ζ – z) ∂f/∂ζ = 0 gelegen sind. Das Lot auf der Tangentialebene: ξ – x : η – y : ζ – z = ∂f/∂ξ : ∂f/∂η : ∂f/ζ heißt Flächennormale. Die Tangentialebene schneidet die Fläche in einer Kurve mit Doppelpunkt im Berührungspunkt; die Tangenten in letzterem oskulieren die Fläche und heißen Haupttangenten. Die Flächenpunkte, in denen die Tangentialebene von der Fläche in einem Doppelpunkt mit Inflexion geschnitten wird und in welchen daher die eine Haupttangente die Fläche dreipunktig berührt, liegen auf einer Kurve, der sogenannten Wendekurve. Von einem Punkt (a, b, c) außerhalb der Fläche geht an dieselbe ein Berührungskegel n (n – 1)ter Ordnung. Durch die Berührungskurve desselben geht auch die Fläche ∂f/∂x (x – a) + ∂f/∂y (y – b) + ∂f/∂z (z – c) = 0, die Polarfläche des Punktes (a, b, c) in bezug auf f = 0 hindurch. Durch den beliebigen Punkt a, b, c gehen 1/2 n (n – 1) (n – 2) (n – 3) Doppeltangenten (Doppellauten) und n (n – 2) (n – 3) Haupttangenten (Rückkehrkanten des Berührungskegels) hindurch. Die Klasse des Kegels ist n (n – 1)2, zugleich die Klasse der Fläche oder die Zahl der durch eine beliebige Gerade an dieselbe zu legenden Tangentialebenen. In einem Doppelpunkt (Knotenpunkt) der Fläche bilden die Tangenten einen Kegel zweiter Ordnung, der in ein Ebenenpaar oder in eine Doppelebene ausarten kann (biplanarer und uniplanarer Knotenpunkt). Die Punkte, deren Polarflächen in bezug auf die Fläche Doppelpunkte besitzen, liegen auf der Hesseschen oder Kernfläche von der Ordnung 4 (n – 2), während der Ort dieser[72] Doppelpunkte selbst die konjugierte Kernfläche von der Ordnung 4 (n – 2)3 ist. Durchschneiden sich zwei Mäntel einer Fläche in einer Kurve, so heißt diese Doppelkurve der Fläche; Rückkehrkurve heißt eine Raumkurve, längs deren sich zwei Flächenmäntel berühren, ohne sich über dieselbe hinaus fortzusetzen; eine geradlinige Rückkehrkurve heißt Rückkehrkante. Beispiel: Eine Raumkurve ist Rückkehrkurve der von ihren Tangenten gebildeten abwickelbaren Fläche.
B. Flächen dritter Ordnung. Dieselben besitzen höchstens vier Doppelpunkte und höchstens eine Doppelgerade; in letzterem Fall sind sie Regelflächen. Zu diesen gehört das Cylindroid: z (x2 + y2) – c x y = 0. Eine Fläche dritter Ordnung ohne Doppelpunkte kann auf die Form gebracht werden: x13 + x23 + x33 + x43 + x53 = 0, wobei die Ebene x1 = 0 ... x5 = 0 das Pentaeder von Sylvester und Steiner bilden; dabei besteht die identische Relation: x1 + x2 + x3 + x4 + x5 = 0. Die beiden Kernflächen fallen zusammen. Eine Fläche dritter Ordnung besitzt 27 Gerade; jede derselben wird von 10 andern geschnitten und dieselben lassen sich in 36 sogenannte Doppelsechssysteme anordnen.
C. Flächen vierter Ordnung. Von denselben sind zu erwähnen: die Steinersche Fläche mit drei Doppelgeraden durch einen Punkt; die Cykliden, welche den unendlich fernen Kreis zum Doppelkegelschnitt haben, die Kummersche Fläche mit 16 Knotenpunkten, von der das Tetraedroid und die Wellenfläche Spezialfälle sind. Letztere hat die Gleichung (x2 + y2 + z2) (a2x2 + b2y2 + c2z2) – a2 (b2 + c2) x2 – b2 (c2 + a2) y2 – c2 (a2 + b2) z2 + a2 b2 c2 = 0.
D. Familien von Flächen. a) Zylinderflächen F(x – a z, y – b z) = 0. Differentialgleichung a p + b q = 1. Regelflächen, deren sämtliche Erzeugende einer Geraden parallel sind. b) Kegelflächen F (x – a/z – c, y – b/z – c) = 0. Differentialgleichung (x – a) p + (y – b) q = z – c. Regelflächen, deren sämtliche Erzeugende durch einen Punkt gehen, c) Umdrehungsflächen F (x2 + y2, z) = 0. Differentialgleichung p y – q x = 0. Sie entstehen durch Drehung einer Kurve um eine Gerade, d) Konoidflächen F (yx, z) = 0. Differentialgleichung p x + q y = 0. Sie werden erzeugt durch eine Gerade, die eine andre schneidet und zu einer Ebene parallel bleibt. e) Regelflächen x = f (α) z + φ (α); y = ψ (α) · z + χ (α). Es befinden sich auf ihnen unendlich viele Geraden. Sie sind abwickelbar, wenn r t – s2 = 0.
E. Krümmung der Flächen. Die Fläche z = f(xy) wird durch eine zur Tangentialebene z = 0 parallele unendlich nahe Ebene z = ε in einem unendlich kleinen Kegelschnitt, der Indicatrix, geschnitten. Je nachdem dieselbe eine Ellipse, ein Parallelenpaar, eine Hyperbel ist, heißt die Fläche im Ursprung elliptisch, parabolisch, hyperbolisch gekrümmt. Die Punkte parabolischer Krümmung befinden sich auf der parabolischen Kurve, die von der Hesseschen Fläche (s. A.) ausgeschnitten wird. Der Krümmungsradius eines Normalschnitts ist dem Quadrat des Durchmessers der Indicatrix, durch den er geht, proportional (s. Eulersche Formel). In den durch die Achsen der Indicatrix gehenden Hauptschnitten erreicht der Krümmungsradius seinen größten bezw. kleinsten Wert (Hauptkrümmungsradien ρ1 und ρ2). Bei Drehungsflächen sind der Krümmungsradius des Meridians und das Stück seiner Normalen bis zur Drehachse die beiden Hauptkrümmungsradien. 1/ρ1ρ2 heißt Krümmungsmaß, 1/ρ1 + 1/ρ2 mittlere Krümmung; dieselbe ist Null bei den Minimalflächen. In den Kreispunkten (Nabelpunkten) ist ρ1 = ρ2, also alle Krümmungshalbmesser der Normalschnitte einander gleich. Eine unendliche Reihe von Kreispunkten auf der Fläche heißt Linie sphärischer Krümmung. Satz von Meunier: Ist ρ der Krümmungsradius eines Normalschnitts, r derjenige eines mit demselben den Winkel ϑ bildenden und durch dieselbe Tangente gehenden schiefen Schnitts, so ist r = ρ cos ϑ Die sphärische Abbildung einer Fläche erhält man, indem man zu allen Flächennormalen parallele Radien einer Kugel zieht; dieselbe ist bei den Minimalflächen konform.
F. Flächenkurven. Haupttangentenkurven (asymptotische Kurven) sind solche Flächenkurven, deren Richtung immer mit derjenigen der Haupttangenten (Asymptoten der Indicatrix) zusammenfällt. Ist f (x, y, z) = 0 die Kurvengleichung, so ist die Differentialgleichung der Haupttangentenkurven
Die Schmiegungsebene fällt in jedem Punkt mit der Tangentialebene der Fläche zusammen. Durch jeden Punkt mit hyperbolischer Krümmung gehen zwei reelle Haupttangentenkurven; in den Punkten der parabolischen Kurve besitzen dieselben Spitzen. Krümmungslinien sind solche Flächenkurven, deren Richtung immer mit derjenigen einer der Hauptachsen der Indicatrix zusammenfällt. Ihre Differentialgleichung ist:
Durch jeden Flächenpunkt gehen zwei zueinander senkrechte Krümmungslinien. Satz von Joachimsthal: Ist eine Krümmungslinie eben (z.B. die Meridiankurve einer Drehungsfläche), so wird ihre Ebene von der Tangentialebene der Fläche längs derselben unter konstantem Winkel geschnitten. Die Krümmungslinie ist alsdann zugleich geodätische Linie (s. unten). Satz von Dupin: Schneiden sich drei Flächen in einem Punkte rechtwinklig und schneiden sie sich paarweise im nächsten Punkt ebenfalls rechtwinklig, so sind die Richtungen der Schnittkurven zugleich Richtungen von Krümmungslinien in jeder. Daher werden die Krümmungslinien der Flächen zweiten Grades durch konfokale Flächen ausgeschnitten. Die Normalen in den Punkten einer Krümmungslinie erzeugen eine abwickelbare Fläche. Die Rückkehrkanten aller dieser zu den Krümmungslinien gehörigen abwickelbaren Flächen bilden die Krümmungszentrafläche (Zentrafläche), auf[73] der die Hauptkrümmungszentra liegen und die im allgemeinen zwei Mäntel besitzt. Die genannten Rückkehrkanten sind zugleich geodätische Linien der Zentrafläche. Geodätische Linien sind solche Flächenkurven, deren Schmiegungsebene immer die Flächennormale enthält. Ihre Differentialgleichung ist:
Sie sind die kürzesten Flächenkurven zwischen zwei Punkten; durch jeden Punkt gehen unendlich viele hindurch. Sie spielen auf der Fläche dieselbe Rolle wie die Geraden in der Ebene; man redet daher von geodätischen Parallelen, Koordinaten, Kreisen, Krümmung u.s.w.
Literatur: [1] Salmon, Analytische Geometrie des Raumes, deutsch von Fiedler, 3. Aufl., 2. Teil, Leipzig 1880. – [2] Stahl, H, und Komerell, V., Die Grundformeln der allgemeinen Flächentheorie, Leipzig 1893. – [3] Joachimsthal, F., Anwendung der Differential- und Integralrechnung auf die allgemeine Theorie der Flächen und der Linien doppelter Krümmung, 3. Aufl., bearbeitet von L. Natani, Leipzig 1890. – [4] Serret, Lehrbuch der Differentialrechnung, deutsch von Harnack, Leipzig 1884, Kap. 9 und 10. – [5] Darboux, Leçons sur la théorie générale des surfaces et les applications géométriques du calcul infinitésimal I–IV, Paris 1887–96. – [6] Knoblauch, Einleitung in die allgemeine Theorie der krummen Flächen, Leipzig 1888. – [7] Gauß, C.F., Allgemeine Flächentheorie, deutsch von Wangerin, 2. Aufl., Leipzig 1900. – [8] Cremona, Grundzüge einer allgemeinen Theorie der Oberfläche in synthetischer Behandlung, deutsch von Curtze, Berlin 1870. – [9] Bianchi, Vorlesungen über Differentialgeometrie, deutsch von Lukat, Leipzig 1899. – [10] Cesaro, Vorlesungen über natürliche Geometrie, deutsch von Kowalewski, Leipzig 1901. – [11] Kommerell, V. und K., Allgemeine Theorie der Raumkurven und Flächen, I–II, Leipzig 1903.
Wölffing.
Buchempfehlung
Lewald, Fanny
Jenny
1843 gelingt Fanny Lewald mit einem der ersten Frauenromane in deutscher Sprache der literarische Durchbruch. Die autobiografisch inspirierte Titelfigur Jenny Meier entscheidet sich im Spannungsfeld zwischen Liebe und religiöser Orthodoxie zunächst gegen die Liebe, um später tragisch eines besseren belehrt zu werden.
220 Seiten, 11.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Romantische Geschichten III. Sieben Erzählungen
Romantik! Das ist auch – aber eben nicht nur – eine Epoche. Wenn wir heute etwas romantisch finden oder nennen, schwingt darin die Sehnsucht und die Leidenschaft der jungen Autoren, die seit dem Ausklang des 18. Jahrhundert ihre Gefühlswelt gegen die von der Aufklärung geforderte Vernunft verteidigt haben. So sind vor 200 Jahren wundervolle Erzählungen entstanden. Sie handeln von der Suche nach einer verlorengegangenen Welt des Wunderbaren, sind melancholisch oder mythisch oder märchenhaft, jedenfalls aber romantisch - damals wie heute. Nach den erfolgreichen beiden ersten Bänden hat Michael Holzinger sieben weitere Meistererzählungen der Romantik zu einen dritten Band zusammengefasst.
- Ludwig Tieck Peter Lebrecht
- Friedrich de la Motte Fouqué Undine
- Ludwig Achim von Arnim Isabella von Ägypten
- Clemens Brentano Geschichte vom braven Kasperl und dem schönen Annerl
- E. T. A. Hoffmann Das Fräulein von Scuderi
- Joseph von Eichendorff Aus dem Leben eines Taugenichts
- Wilhelm Hauff Phantasien im Bremer Ratskeller
456 Seiten, 16.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum