Online-Bibliothek

Mathematische Zeichen

[335] Mathematische Zeichen, in der Mathematik übliche Abkürzungen.

Die gebräuchlichsten sind: = gleich; ≡ identisch gleich, kongruent (in der Zahlentheorie); > größer als; < kleiner als; 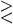oder =|= nicht gleich; ~ ähnlich; ≅ kongruent (in der Geometrie); + plus (Additionszeichen); – minus (Subtraktionszeichen); · oder × mal (Multiplikationszeichen); : durch (Divisionszeichen) oder: verhält sich zu (in Proportionen); √ Wurzelzeichen; ∞ unendlich; ! Fakultät (n! = Produkt der n ersten Zahlen); () Zeichen der Binomialkoeffizienten, z.B.

< oder ∢ oder ∧ Winkel; ∩ Bogen; Δ Dreieck; ∥ parallel; ⊥ senkrecht; 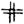gleich und parallel; | | absoluter Betrag (z.B. |–a| = a); ± plus oder minus; ∫ Integralzeichen. Hierzu kommen noch die Klammern (); []; {}. – Wenn auch die Wahl der Buchstaben in mathematischen Ausdrücken willkürlich ist, so ist es doch üblich, für gewisse Größen bestimmte Buchstaben zu wählen. Die häufigsten dieser stehenden Bezeichnungen sind:

a, b, c ... Koeffizienten; c Konstante; d Zeichen der Differentiation, Differenz in arithmetischen Reihen, Zahl der Doppelpunkte einer Kurve; ∂ Zeichen der partiellen Differentiation; e Basis des natürlichen Logarithmensystems, Exzentrizität (bei Kegelschnitten), Einheit (in der Zahlentheorie), endliche Zahl; f Reibungskoeffizient, Funktion; g Beschleunigung durch die Schwere; h Höhe; i Quadratwurzel aus der negativen Einheit (Zeichen der imaginären Zahlen); j imaginäre dritte Einheitswurzel; k Klasse der Kurven, Modul der elliptischen Integrale; l Zeichen des natürlichen Logarithmus; m Mittellinie, Masse; n unbestimmte Zahl; o Ordnung einer Kurve; p Geschlecht einer Kurve, p-Funktion (s. Sigmafunktionen), ∂z/∂x, Parameter der Kegelschnitte, Beschleunigung; p, q, r Linienkoordinaten im Raum; q Zinsfaktor, Rang, ∂z/∂y; Querschnitt; r Rente, Radius, ∂²z/∂x², Substitution, Zahl der Rückkehrpunkte einer Kurve, Torsionsradius; s Summe, Kurvenbogen, ∂²z/∂x∂y, Potenzsummen der Wurzeln einer Gleichung; t Zeit, Schwerlinie, ∂²z/∂y², Zahl der Doppeltangenten einer Kurve; u Glieder von Reihen; u, v, w Linienkoordinaten in der Ebene; v Geschwindigkeit; w Wahrscheinlichkeit, Zahl der Wendepunkte: x, y, z Unbekannte, Veränderliche, Punktkoordinaten; z komplexe Veränderliche.

α, β, γ bekannte Winkel, Koeffizienten; δ beliebig kleine Größe, Zeichen der Variation, Zeichen des Aronholdschen Prozesses, ε ± 1, beliebig kleine Größe, beliebig kleiner Parameter; ζ Zetafunktion (s. Sigmafunktionen), Veränderliche; η Veränderliche; ϑ Winkel, Thetafunktion, echter Bruch, χ Modul der elliptischen Integrale, Linienkoordinate im Raum; λ Parameter; ξ Veränderliche; π Verhältnis des Kreisumfangs zum Durchmesser, Linienkoordinate im Raum; ρ Radius, Proportionalitätsfaktor, Krümmungsradius, Linienkoordinate im Raum; σ Sigmafunktion; φ Winkel, adjungierte Kurven, zahlentheoretische Funktion; ψ, χ Winkel; ω Periode, homogenisierende Veränderliche, Winkelgeschwindigkeit, Wälzungswinkel bei Rouletten; ώ unendlich wachsende Zahl.

B Bernoullische Zahlen; C Konstante, Eulersche Konstante (0,57721566 ...); D Determinante, Diskriminante; E vollständiges elliptisches Integral II. Gattung, Eulersche Zahlen; F Brennpunkt, Fläche, hypergeometrische Reihe, elliptisches Integral I. Gattung; G Gruppe; J Zylinderfunktion; K vollständiges elliptisches Integral I. Gattung, Kreis, Kraft, Kegelschnitt; L gerade Linie; M Modul; O Ursprung, Oberfläche; P Punkt, Kugelfunktion; Q Gewicht; R Restglied bei Reihen, Resultante; S Substitution; T Tangente, lebendige Kraft; U Arbeit; V Potential, Volumen; X infinitesimale Transformation.[335]

Β Betafunktion; Γ Gammafunktion; Δ Deltaamplitude, Transformationsdeterminante, Größe, die gegen Null konvergiert; Π Produkt, elliptisches Integral III. Gattung; Σ Summenzeichen; Ω Omegaprozeß; P Potenzreihe.

Auch einige Buchstabenverbindungen dienen als Abkürzungen: z.B. sin, cos, tg, cotg, sec, cosec für die goniometrischen und arc sin u.s.w. für die cyclometrischen Funktionen; log oder lg Logarithmus. Weitergehende Abkürzungen finden sich in den mathematischen Zeichensprachen (s. Literatur).

Literatur (für Zeichensprachen): [1] Schröder, Vorlesungen über die Algebra der Logik, I-III, Leipzig 1890–95. – [2] Peano, Notations de logique mathématique, Turin 1894. – [3] Frege, Begriffsschrift, Halle 1879.

Wölffing.