Online-Bibliothek

Zentrifugalkraft

[897] Zentrifugalkraft (Fliehkraft, Schwungkraft), die aus dem Beharrungsvermögen entspringende Kraft, mit der ein in krummliniger Bahn bewegter Körper der Krümmung seiner Bahn widerstrebt.

Fig. 1. Zentriefugalkraft.

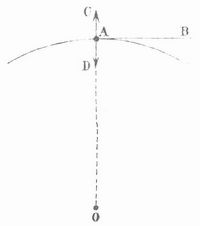
Wenn z. B. eine Lokomotive auf gekrümmter Bahn dahinfährt, so hat sie vermöge ihrer Trägheit in jedem Augenblick das Bestreben, entlang der Berührungslinie A B (Fig. 1) der Bahn geradeaus zu gehen und demnach eine Richtung einzuschlagen, die sie von dem Krümmungsmittelpunkt O der Bahnkurve, entfernen würde; dieses Bestreben äußert sich durch einen Druck A C, den die Lokomotive vermittelst der Radkränze nach außen hin, vom Mittelpunkt weg, auf die an der gewölbten Seite der Bahnkurve liegende Schiene ausübt; dieser Druck oder diese Kraft heißt die Z. Ihr wirkt von seiten der unnachgiebigen Schiene eine gleichgroße nach innen (gegen den Mittelpunkt hin) gerichtete Kraft A D entgegen, die als Zentripetalkraft die Lokomotive zwingt, auf der Kurve zu bleiben. Zentripetalkraft und Z. sind als Wirkung und Gegenwirkung einander stets gleich und entgegengesetzt. Die Z. macht sich bei jeder krummlinigen Bewegung geltend. Wird z. B. ein am Ende einer Schnur befestigter oder in eine Schleuder gelegter Stein rasch im Kreis herumgeschwungen, so erleidet die Schnur eine Spannung, die, als Zentripetalkraft nach einwärts wirkend, den Stein nötigt, von der geradlinigen Bewegung abzuweichen und eine Kreislinie zu beschreiben, und als Z. nach außen hin einen Zug auf die Hand ausübt, die das andre Ende der Schnur festhält. Reißt der Faden plötzlich ab, so hört mit der Zentripetalkraft auch die Z. plötzlich auf, und der Stein fliegt, nunmehr nur noch der Trägheit gehorchend, in der Richtung der Berührungslinie (Tangente) davon mit der Geschwindigkeit, die er im Augenblick des Loslassens gerade besaß. Wenn Mühlsteine, Schleifsteine, Schwungräder mit zu großer Geschwindigkeit sich um ihre Achse drehen, so kann die Z. das Zerreißen derselben herbeiführen, und die Stücke werden in tangentialer Richtung fortgeschleudert. Praktische Verwendung findet die Z. in den Zentrifugalmaschinen.

Die Kraft, die nötig ist, um einen bewegten Körper von der geraden Linie abzulenken, ist um so größer, je größer die Wucht oder lebendige Kraft des dahineilenden Körpers ist, und je stärker die Bahn gekrümmt werden soll. Die Wucht eines bewegten Körpers ist aber seiner Masse (m) und dem Quadrat seiner Geschwindigkeit (v) proportional, und die Krümmung einer Kurve steht im umgekehrten Verhältnis zum Krümmungshalbmesser OA = r. Es ergibt sich also, daß die Z. und die ihr gleiche Zentripetalkraft im geraden Verhältnis zur Masse und zum Quadrat der Geschwindigkeit des bewegten Körpers und im umgekehrten Verhältnis zum Krümmungshalbmesser der Bahn steht, oder es ist C = mv²/r oder, falls w die Winkelgeschwindigkeit bedeutet, C = m.r.w². Bei gleichförmigen Kreisbewegungen gibt man gewöhnlich statt der Geschwindigkeit die Umlaufszeit (t) an, d. h. die Zeit, die der Körper braucht, um den ganzen Kreisumfang (2πr) zurückzulegen; die Geschwindigkeit wird alsdann erhalten, wenn man den Kreisumfang durch die (in Sekunden ausgedrückte) Umlaufszeit dividiert (v = 2πr/t); dieselbe steht demnach zu dem Halbmesser des Kreises in geradem, zur Umlaufszeit in verkehrtem Verhältnis. Mit Rücksicht hierauf läßt sich der obige Satz auch so ausdrücken: die Z. oder die Zentripetalkraft ist der Masse des bewegten Körpers und dem Halbmesser der Kreisbahn direkt, dem Quadrat der Umlaufszeit umgekehrt proportional, oder es ist C = 4π²mr/t². Die durch die tägliche Umdrehung der Erde erzeugte Z. ist an jedem Ort senkrecht zur Erdachse und von dieser weg gerichtet; sie trägt mit bei zu der Verminderung der Schwerkraft von den Polen nach dem Äquator hin, die sich durch Pendelbeobachtungen (s. d.) nachweisen und messen läßt. Da für alle Punkte der Erdoberfläche die Umlaufszeit die gleiche ist, nämlich 24 Stunden (Sternzeit), so ist die Z. an jedem Orte dem Halbmesser des Parallelkreises proportional, den der Ort während der täglichen Umdrehung beschreibt. Am Äquator, wo sie der Schwerkraft gerade entgegenwirkt, ist sie am größten und beträgt ¹/₂₈₉ der Schwerkraft. Würde sich die Erde 17mal schneller um ihre Achse drehen, als sie es wirklich tut, so würde die Z. 17×17 oder 289mal größer sein und die Schwerkraft am Äquator völlig aufheben.

Fig. 2. Zentriefugalmaschine.

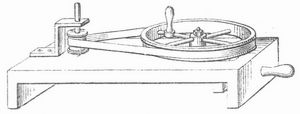
Zum Nachweis der Z. und ihrer Gesetze dient die Zentrifugalmaschine (Schwungmaschine, Fig. 2). Zwei Räder mit parallelen Achsen, ein größeres,[897] das Schwungrad, und ein kleineres, dessen Achse zum Aufstecken verschiedener Versuchsvorrichtungen eingerichtet ist, sind durch eine um ihre ausgehöhlten Umfänge gelegte Schnur oder einen Riemen ohne Ende miteinander verbunden, so daß sich die Achse des kleinen Rades mit großer Geschwindigkeit dreht, wenn das große mittels einer Kurbel in Umdrehung versetzt wird. Es werde z. B. auf die Achse ein Holzrähmchen aufgesetzt, in dem ein wagerechter Metalldraht ausgespannt ist; auf diesem sind zwei durchbohrte Metallkugeln, die durch einen Draht oder durch Schnüre miteinander verbunden sind, leicht verschiebbar; befinden sich die beiden Kugeln auf verschiedenen Seiten der Drehungsachse, so werden sie bei der Umdrehung vermöge der Z. auseinander fahren, und diejenige Kugel, deren Z. die größere ist, wird die andre nach sich ziehen; man findet nun leicht eine solche Stellung der Kugeln diesseit und jenseit der Achse, daß bei der Umdrehung die Kugeln in Ruhe bleiben, indem ihre Zentrifugalkräfte sich das Gleichgewicht halten; dies tritt ein, wenn ihre Entfernungen von der Drehungsachse sich umgekehrt verhalten wie ihre Massen, oder wenn die Produkte aus den Massen und den Halbmessern der durchlaufenen Kreise für beide Kugeln gleich sind. Bei gleicher Umlaufszeit verhalten sich also die Zentrifugalkräfte wie die Massen und wie die Halbmesser der Kreisbahnen, wie das oben mitgeteilte Gesetz es verlangt. Wird ferner auf die Achse der Zentrifugalmaschine eine vertikale Welle aufgesteckt, woran zwei Kugeln an Drähten, die sich oben in Scharnieren drehen, pendelartig herabhängen, so entfernen sich die Kugeln mit wachsender Umdrehungsgeschwindigkeit immer mehr von der Achse und heben ein längs der Achse verschiebbares Gewicht; diese Einrichtung findet als Zentrifugalregulator bei Dampfmaschinen Verwendung; ferner in Verbindung mit einer Federwage als Tachometer (Geschwindigkeitsmesser) zur Bestimmung der Tourenzahl in 1 Sekunde oder Winkelgeschwindigkeit. Ein kreisförmig gebogener elastischer Metallstreifen, der auf eine lotrechte Welle lose aufgesteckt ist, so daß diese als sein vertikaler Durchmesser erscheint, wird durch die Z., die an den von der Achse am weitesten entfernten Endpunkten seines horizontalen Durchmessers am stärksten wirkt, zu einer Ellipse auseinander gezogen und versinnlicht dadurch die Entstehung der Abplattung der Erde.