Potenz

[435] Potenz (v. lat.), 1) Macht, Mächtigkeit, Gewalt, Kraft; P. eines Mannes, die Zeugungskraft; P. einer Maschine, die Kraft, welche sie leistet; 2) jede Einwirkung auf den lebenden Körper, welche das Leben unterhält, od. auch modificirt. Daher bei Lebenserscheinungen Potenzirung, die Erhebung eines Naturvorganges, Depotenzirung, eine Herabsetzung eines solchen; so sagt man, daß das Thier eine potenzirte Pflanze, die Pflanze ein depotenzirtes Thier sei, u. in dieser Hinsicht ist die Geschlechtsliebe ein potenzirtes, das Leben im hinfälligen Greisesalter ein depotenzirtes Leben; 3) ein Product aus lauter gleichen Factoren. Ein solcher Factor heißt die Grundzahl od. Dignand, die Anzahl der Factoren aber der Exponent (Index) der P.; dieser wird in kleiner Schrift dem Dignanden zur Rechten oben gesetzt, z.B. a⁵ = a. a. a. a. a. Dies wird gelesen a in der 5. (nämlich P.) od. a hoch 5. Eine solche P. finden heißt die Grundzahl auf die P. erheben, sie potenziren. Eine jede Zahl wird in dieser Beziehung als erste P. betrachtet; mit sich selbst multiplicirt, wird sie dann zur zweiten P. (Quadratzahl, s.d.); durch Wiederholung der Multiplication durch die 1. Zahl zur dritten P. (Cubikzahl, s. Cubus 2). Bis hierher reichen die P-en im Räumlichen (in der Geometrie). Eine Linie von 10 Fuß Längenmaß gibt in der 2. P. 100 Quadratfuß (im Flächenmaß), in der 3. P. 1000 Cubikfuß (cubisches Maß). In der allgemeinen Mathematik aber gehen die P-en ins Unendliche. Hauptsächlichste Sätze: 1^m = 1; a⁰ = 1; 0^m = 0; (ab)^m = a^m. b^m;

Grundlage der ganzen Potenzenlehre sind folgende drei Sätze: a^m. aⁿ = a^m+n;

= a^m-n; (a^r)^s = a^r.s. Stellt man noch für P-en mit negativen u. mit gebrochenen Exponenten die durch folgende beiden Formeln

gegebenen Definitionen auf, so gelten vorstehende Sätze für jeden möglichen rationalen od. irrationalen Werth der Exponenten mit der einzigen Ausnahme, daß o^-n = ∞. Ist die Grundzahl der P. negativ u. dabei der Exponent eine gerade ganze Zahl od. ein Bruch mit geradem Zähler, so ist der Werth der P. positiv; ist aber dabei der Exponent eine ungerade Zahl od. ein Bruch, dessen Zähler u. Nenner ungerade sind, so ist der Werth der P. negativ, nach dem Satze, daß eine gerade Anzahl negativer Factoren ein positives Product liefern, eine ungerade Anzahl dagegen ein negatives.[435] Ist endlich bei negativer Grundzahl der Exponent ein Bruch mit geradem Nenner, so ist der Werth der P. imaginär. Vom Potenziren gibt es zwei Umkehrungen: man kann entweder nach der Grundzahl fragen, deren nte P. gleich a ist, u. diese heißt dann nte Wurzel aus a, geschrieben 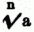= x, wo dann xⁿ = a sein muß; od. man kann nach dem Exponenten der P. fragen, zu welcher b erhoben werden muß, um a zu erhalten, u. dieser heißt dann der Logarithmus von a zur Basis b, geschrieben log a_b = x, wo dann b^x = a; letztere Rechnungsart heißt auch a nach (od. durch) b exponentiren. 4) Potenz der Hyperbel, die Größe ¹/₄ (a² + b²), wenn a u. b die Halbachsen der Hyperbel sind. Transformirt man die gewöhnliche Mittelpunktsgleichung a²y² – b²x² = – a² b² der Hyperbel für schiefwinkelige Coordinaten, so daß die Asymptoten die Coordinatenachsen werden, so findet man xy = ¹/₄ (a² + b²) = der P. d. H. Da die schiefwinkeligen Coordinaten für den Scheitel der Hyperbel einander gleich sind, so folgt zugleich, daß die P. d. H. das Quadrat der Linie ist, welche durch den Scheitel parallel zu der einen Asymptote gelegt u. durch die andere Asymptote begrenzt wird.