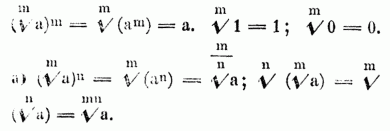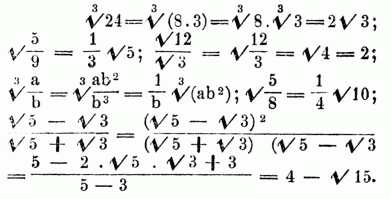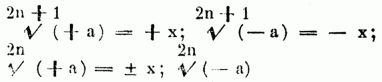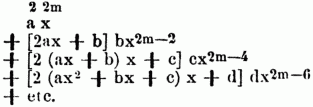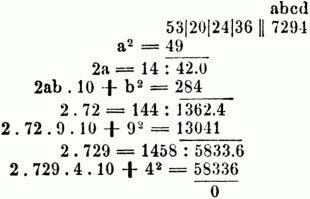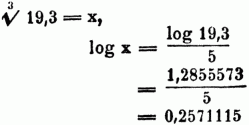Wurzel
[436] Wurzel (Radix), 1) jeder Theil der Pflanze, welcher nach unten zu wachsen strebt, also nach dem Dunkel, indem er in die Erde etc. hinabwächst od. auf einem anderen Körper festsitzt, welcher aber nicht blos dazu dient, die Pflanze in ihrem Boden festzuhalten, sondern auch vorzüglich derselben Nahrung zuzuführen u. auch Stoffe, welche für den Organismus der Pflanze nicht mehr tauglich sind, auszuleeren. Da diese. Stoffe, ob sie gleich der Pflanze, von welcher sie ausgeschieden worden, u. auch manchen anderen gleichartigen unnütz od. schädlich sind, so beweisen sie sich doch für manche anderen Gewächse als unschädlich u. selbst nützlich u. nahrhaft. Hierauf beruht der Nutzen u. die Nothwendigkeit des Fruchtwechsels in der Landwirthschaft. Im gemeinen Leben unterscheidet man: Pfahlwurzeln (Radices palares), welche in die Tiefe dringend, stammartig Äste u. Zweige abgeben; Nestwurzeln, welche holzig sind, aber sich nur an der Oberfläche verästeln, ohne senkrecht in die Tiefe zu dringen; Thauwurzeln, welche aus lauter zarten, flachliegenden Fasern bestehen. Ferner noch einjährige (annuae), zweijährige (biennes) u. ausdauernde (perennes) W-n. Die eigentliche W. entwickelt sich im Keime aus dem Würzelchen, also unterhalb des Federchens od. des Stängelchens (s. Samen) nach unten zu, wird niemals grün, ist demnach hinsichtlich des Wachsthums u. der Farbe dem Stängel der Pflanze gerade entgegengesetzt u. unterscheidet sich hierdurch von dem in der Erde befindlichen, in mehrfacher Hinsicht der W. ähnelnden Theil des Stängels, dem Rhizome od. Wurzelstock, der Zwiebel, dem Knollen etc., welche früher zur W. gerechnet wurden u. welche man Mittelstock, wie die W. Unterstock u. den Stängel Oberstock nennen kann. Die wahre W. ist a) ihrer Gestalt nach: fadenförmig (R. filiformis), dünn, gleichdick; walzenförmig (cylindrica, teres), im Querdurchschnitt kreisförmig, gleichdick, in die Länge gezogen, nicht allzudünn; rüben- od. spindelförmig (fusiformis), im Querdurchschnitt kreisförmig, nach oben u. unten dünner werdend u. in eine Spitze auslaufend; rettigförmig (rapiformis), kugelförmig, nach unten aber plötzlich verdünnt u. zugespitzt; kugelförmig (globosa), rund, wie eine Kugel; länglich (oblonga), wenn die kugelförmige W. mehr in die Länge gezogen ist; brod- od. kuchenförmig (placentaeformis), wenn sie dagegen von oben u. unten zusammengedrückt ist; perlenschnur- od. rosenkranzförmig (moniliformis), mit rundlichen, gleich den Kugeln eines Rosenkranzes an einander liegenden Anschwellungen; hängend (pendula), wenn knollig verdickte Stellen durch dünnere, fadenförmige Fasern zusammenhängen. b) Ihrer Verästelung nach unterscheidet man: die einfache od. ungetheilte (R. simplex od. indivisa); die verästelte (ramosa); sehr verästelte (ramosissima); wenig (parum ramosa), od. kaum verästelte (subramosa); die pfahlästige (palariramosa), mit starkem, gerade abwärtssteigendem Haupttheil, von welchem Seitenäste abgehen. c) Ihrer Richtung nach: senkrecht (R. perpendicularis), gerade abwärts steigend; wagerecht (horizontalis), der Oberfläche des Bodens parallel laufend; gerade (recta), od. gebogen (flexuosa od. flexa). d) Hinsichtlich ihrer Substanz: holzig (lignosa), nur diese treiben Blattaugen, werden deshalb auch von Manchen als Caudex bezeichnet; fleischig (carnosa); markig (medullosa). Als Neben-, Adventiv- od. secundäre W-n (R. adventitiae, R. successivae od. R. secundariae), bezeichnet man solche, welche zwar übrigens alle Eigenschaften einer wahren W. haben, aber an der Basis od. auch an einer höheren Stelle des Stängels entspringen. So die an den Gelenken kriechender Stängel, ferner die Luftwurzeln (Radices aëreae), welche aus dem oberen Theile der Stängel u. Äste mancher Pflanzen hervortreten, bisweilen ohne die Erde zu berühren, bisweilen auch bis auf den Boden herabhängend u. in denselben eindringend, wie z.B. bei Rhizophora, Adansonia, Pothos, Pandanus etc. Manche Pflanzen bilden an gewissen Stellen des Stängels eine Anschwellung der Rinde, welche sich platt an die Rinde anderer Gewächse od. an Steine anlegt, durch Erhebung der Ränder einen luftleeren Raum erzeugt u. auf diese Weise fest ansitzt. Aus dieser Saugwarze (Haustorium) treten Nebenwurzeln hervor, welche in die fremde Pflanze od. das Gestein eindringen u. Saugwurzeln (R. haurientes) heißen, wenn sie in das Gewebe einer Pflanze mit ihrer Saugwarze ganz eindringen, wie bei Cuscuta u. Lathraea; Klammer- od. Haftwurzeln (R. alligantes), wenn sie sich an einer Pflanze festsetzen, ohne in das Gewebe völlig einzudringen od. organisch in dieselbe fortzusetzen, wie bei Hedera helix od. Tecoma radicans. Die, welche in das Gewebe einer anderen Pflanze so ganz eindringen u. verschmelzen, daß sie keine besondere W. zu besitzen erscheinen, nennt man falsche W-n(Radices nothae), wie z.B. bei Rafflesia, Brugmansia, Viscum, Loranthus etc. Bei manchen Wasserpflanzen entstehen an der Basis des blattartigen Stängels Nebenwurzeln, welche sich blos in das Wasser senken, schwimmende W-n (R. natantes). Oft reißen diese beim Hervorbrechen eine Zellenschicht los, welche dann als Haube (Calyptra) auf ihrer Spitze sitzen bleibt. Bei vielen Pflanzen, namentlich Monokotyledonen, verlängert sich das Würzelchen des Keimes nicht; es ist von einer Hülle umschlossen (Plantae endorrhizae), welche von Nebenwurzeln durchbrochen wird, die nun an der Basis des Stängels sitzen u. während des ganzen Lebens der Pflanze die wahre W. vertreten. Solche W-n sind entweder haarförmig (R. capillares), aus lauterfeinen Fasern, od. faserig (fibrosae), aus etwas stärkeren Fasern bestehend, von denen dünne Fasern seitlich ausgehen; strangförmig (funiformes), aus lauter einfachen, stärkeren, gleichdicken Fasern gebildet;[436] büschelig (fasciculatea od. fasciculares), wenn mehre längliche od. walzenförmige fleischige, knollige W-n, aus einem Punkte entstanden, neben einander liegen; büschelästig (fasciculato-ramosae), wenn mehre ziemlich starke, ästige Fasern neben einander aus der Basis des Stängels entspringen. An den Spitzen mancher W-n finden sich sie bedeckende, verkehrt kegelförmige, dünne häutige Theile, Schienen (Ocreae). 2) Die eßbaren W-n verschiedener Gewächse, z.B. Möhren, Pastinaken, Petersilienwurzeln etc.; 3) der Ort eines Dinges, wo dasselbe an einen anderen Gegenstand angewachsen ist; 4) der unterste Anfangstheil eines Organes od. Körpertheiles; W. der Epiglottis, s. Kehlkopf A) f). W. der Sphenoidalflügel (Radix alae majoris ossis sphenoidei), der Theil, wo die Flügel des Keilbeines von dem Körper desselben in die Höhe steigen. W. des flügelförmigen Fortsatzes (Radix processus pterygoidei), der vorwärts flache, hinterwärts rauhere Theil des genannten Fortsatzes, wo derselbe von dem großen Keilbeinflügel abgeht. W. des Olecranums (Radix olecrani), die Stelle, wo das Olecranum am oberen Ende des Ellenbogenknochens seinen Anfang nimmt. W. der Nägel, s.u. Nägel 1). W. der Zähne, s.u. Zähne. 5) Der unterste Theil eines Berges, s.d.; 6) an Strebepfeilern der an die Mauer anstoßende Theil derselben; 7) der Theil eines Wortes, welcher nach Ablösung aller Bildungselemente u. Bildungssylben übrig bleibt u. in welchem der Stammbegriff des Wortes liegt, z.B. von entschuldigen ist die W. schul. Daher heißen in der Grammatik wurzelhafte Buchstaben die, welche zur W. gehören od. überhaupt in W-n vorkommen können; 8) die irgendvielte W. aus einer gegebenen Zahl bezeichnet diejenige Zahl, deren ebensovielte Potenz gleich der gegebenen Zahl ist. So ist 9 die 2. W. aus 81, weil 9, mit 2 protenzirt (9 . 9) 81 gibt; eben so 7 die 3. W. aus 343, weil die 3. Potenz von 7 (7 . 7 . 7) = 343 ist. Die 2., 3. u. 4 W. nennt man auch bezüglich die Quadrat-, Cubik- u. Biquadratwurzel. Daß die mte W. aus a zu suchen od. zu ziehen ist, deutet man durch 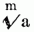 an, u. sagt auch: a sei durch m zu radiciren. Das Zeichen (Wurzelzeichen, Radicalzeichen) √ ist ursprünglich ein lateinisches r (radix). m wird der Wurzelexponent, a aber der Radicand genannt. Die mit dem Wurzelzeichen behafteten Größen nennt man auch Wurzelgrößen. Wird der Exponent weggelassen, so versteht man darunter stillschweigend die Quadratwurzel, so ist
an, u. sagt auch: a sei durch m zu radiciren. Das Zeichen (Wurzelzeichen, Radicalzeichen) √ ist ursprünglich ein lateinisches r (radix). m wird der Wurzelexponent, a aber der Radicand genannt. Die mit dem Wurzelzeichen behafteten Größen nennt man auch Wurzelgrößen. Wird der Exponent weggelassen, so versteht man darunter stillschweigend die Quadratwurzel, so ist 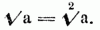 . Fundamentalsätze für die Rechnung mit W-n. Radication u. Potenzirung mit einerlei Zahl heben als entgegengesetzte Rechnungsarten einander auf.
. Fundamentalsätze für die Rechnung mit W-n. Radication u. Potenzirung mit einerlei Zahl heben als entgegengesetzte Rechnungsarten einander auf.
Daher darf man, ohne einen Fehler begehen, bei
die Klammern weglassen u. 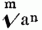 schreiben. Beispiele:
schreiben. Beispiele:
Der Fall b) führt, wenn die Division nicht aufgeht, auf Potenzen mit gebrochenen Exponenten od. sogenannten Bruchpotenzen. Es bedeutet demnach eine Potenz mit gebrochenem Exponenten, daß die sovielte W. aus der Grundzahl, als der Nenner angibt, auf die sovielte Potenz zu erheben ist, als der Zähler anzeigt.
Nun läßt sich leicht mit Hülfe des Vorigen zeigen, daß alle für ganze Potenzexponenten geltende Sätze auch noch für gebrochene wahr sind; es läßt sich demnach die ganze Wurzelrechnung auch in eine bloße Potenzenrechnung verwandeln. Analog mit den Resultaten im Artikel Potenz ergibt sich: Jede ungerade W. aus einer positiven od. negativen Zahl ist bezüglich positiv od. negativ; jede gerade W. aus einer positiven Zahl ist sowohl positiv, als negativ; jede gerade W. aus einer negativen Zahl aber kann weder positiv noch negativ sein u. wird daher umöglich od. imaginär genannt, wogegen die positiven od. negativen Zahlen reelle heißen. Bezeichnen demnach a u. x absolute Zahlen, so ist
imaginär. Die Ausdrücke der letzteren Art verwarf man früher als ohne Bedeutung, allein in der neueren Analysis sind sie als Größenformen, welche denselben Gesetzen der Rechnung unterliegen wie die reellen, von größter Wichtigkeit geworden, theils als wesentliche Abkürzungsmittel bei sehr vielen Entwickelungen, theils um den inneren Zusammenhang von Formen nachzuweisen, welche scheinbar nichts mit einander gemeinschaftlich haben. Jeder imaginäre Wurzelausdruck läßt sich auf die Form h + k √ – 1 bringen, wo h u. k reelle Größen bezeichnen. Hieraus sieht man, daß die Rechnungen mit imaginären Formen sich zuletzt auf Rechnungen mit √ – 1 reduciren. Deshalb ist dieser Ausdruck √ – 1 der Kürze wegen (zuerst von Gauß) mit dem Buchstaben i bezeichnet worden. Auch hat Gauß einen geometrischen Sinn dieser imaginären Größen nachgewiesen, denn während die positiven u. negativen Zahlen Längen auf einer geraden Linie nach der einen u. entgegengesetzten Richtung bezeichnen, drücken die imaginären Zahlen seitliche Abstände von jener Geraden aus, daher sie auch laterale Größen genannt werden. Numerische Wurzelausziehung, d.h. Verfahrungsweisen, ausgegebenen bestimmten Zahlen eine irgendvielte W. wirklich darzustellen, entweder genau, od., wenn dies[437] nicht geht, mit beliebiger Annäherung. Um die Quadratwurzel aus einer gegebenen Zahl zu ziehen, muß man die Form aufsuchen, welche das Quadrat eines Ausdruckes, wie etc.
erhält. Sie ist, wenn man die bekannten bei der Quadratwurzelausziehung anwendbaren Rechnungsvortheile mit in Erwägung zieht, folgende:
Nun möge x die Grundzahl unseres Zahlensystems also 10, a, b, c, d aber einzifferige Zahlen bedeuten, so daß z.B. in 7294 m = 3, a = 7, b = 2, c = 9, d = 4 ist; dann ist nach dem vorigen das Quadrat von 7294 = 72 . 1000000 + 2 . 7 . 2 . 100000 + 22 . 10000 + 2 . 72 . 9 . 1000 + 92. 100 + 2 . 729 . 4 . 10 + 42. Hätte man also umgekehrt aus 53202436 die Quadratwurzel auszuziehen, so würde man zunächst die Millionen abgrenzen, in unserem Falle 53, u. aus ihnen die Quadratwurzel ziehen, also hier a = 7; den Rest 4 hat man dann zu den Hunderttausenden zu schlagen u. in diese mit 25 zu dividiren um b zu finden, doch hat man dies b so zu bestimmen, daß sich auch noch b2 vom Reste der Hunderttausende nebst den Zehntausenden abziehen läßt. In unserem Falle gibt also die Division mit 2 . 7 = 14 in 42 nicht 3, weil sich 32 nicht noch von den Zehntausenden würde abziehen lassen, man muß vielmehr b = 2 nehmen. Den Rest der Zehntausende schlägt man zu den Tausenden, dividirt mit 2a . 10 + b u. findet dadurch c u.s.f. Die Rechnung stellt sich also so:
Bei Zahlen, deren W. sich nur näherungsweise angeben läßt, hat man, um diese bis auf 20 Bruchziffern zu berechnen, nur für n Bruchziffern das gewöhnliche Verfahren anzuwenden, die übrigen n Ziffern aber kann man durch bloße Division mit dem letzten Divisor in dem letzten Rest finden, indem man bei jeder Division von der ersten an nach u. nach 1, 2, 3,.. letzten Ziffern des Divisors wegwirft u. an keinen Rest eine Null hängt. Um die Cubikwurzel aus einer Zahl zu ziehen, bildet man zunächst eine Tafel der Cuben aller ganzen Zahlen von 1 bis 9. Aus dem eigenthümlichen Verfahren, eine mehrzifferige Zahl zum Cubus zu erheben, ergibt sich das für die Ausziehung der Cubikwurzel. So wie dort die einzeln erhaltenen Producte, zusammen addirt werden mußten, um den Cubus zu erhalten, so müssen hier dieselben zu suchenden Stücke nach u. nach von dem gegebenen Cubus subtrahirt werden. Aus jeder gegebenen ganzen Zahl die Cubikwurzel zu ziehen: a) man schneide, rechts von den Einern anfangend, in derselben je drei Ziffern ab, so oft es angeht. Jede solche Abtheilung heißt eine Klasse; die höchste Klasse hat oft nur zwei od. eine Ziffer; b) suche in der Tafel den größten Cubus, welcher sich von der Zahl in der höchsten Klasse subtrahiren läßt, so ist die zu demselben gehörige W. die höchste Ziffer der verlangten Cubikwurzel, sie heiße r1; c) hänge an den Subtractionsrest die drei Ziffern der nächst niedrigeren Klasse; d) man bilde: 3r12 u. dividire damit in die Hunderte der unter c geschriebenen Zahl, also mit Weglassung der beiden letzten Ziffern derselben; e) die gefundene ganze Zahl des Quotienten ist die zweite Ziffer der gesuchten W., sie heiße s; f) man bilde das Product 3r12s u. schreibe es mit seiner letzten Ziffer unter die Hunderte der Zahl in c, ferner das Product 3r1s2 u. schreibe es unter das vorige Product, jedoch eine Stelle nach rechts ausgerückt, endlich s3, welches man wieder um eine Stelle nach rechts gerückt untersetzt, so daß es mit seiner letzten Ziffer unter die letzte. Ziffer der Zahl in c zu stehen kommt, addire die drei Posten 3r12 s, 3r1 s2 u. s3 u. subtrahire die Summe von der Zahl in c; g) zum Reste füge man die drei Ziffern der nächsten Klasse, betrachte r1 . 10 + s als eine Zahl, welche man r2 nenne u. verfahre mit ihr wie mit r1 unter d) e) u. f), um die nächste Ziffer der gesuchten W. zu finden; h) das beschriebene Verfahren setzt man bis zur letzten Klasse der gegebenen Zahl fort. Bleibt nach der Subtraction von. der letzten Klasse noch ein Rest, so läßt sich die Cubikwurzel nie völlig, aber doch so genau darstellen, daß der Fehler weniger beträgt, als jede Größe, welche sich angeben läßt Man mache zur Rechten der zuletzt erhaltenen Ziffer in der W. das Komma, hänge an den letzten Rest jedesmal drei Nullen u. verfahre mit der Wurzelausziehung wie vorher. Dann ist, wenn die Rechnung irgendwo abgebrochen wird, der Fehler in der W. kleiner, als die Einheit der letzten Ziffer in der W. Hat die gegebene Zahl die Gestalt eines Decimalbruches, so schneide man rechts von den Einern eben so je drei Ziffern ab, wie es vorhin links geschah, ergänze, wenn es nöthig ist, in der niedrigsten Klasse die fehlenden Stellen durch Nullen u. verfahre wie sonst. Das Komma in der W. muß zur Rechten derjenigen Ziffer gemacht werden, welche zu der Klasse gehört, in welcher die Einer der gegebenen Zahl stehen. Die Ausziehung aller W-n, welche auf verhältnißmäßig wenige Bruchstellen berechnet werden sollen, kann man sich erleichtern durch Hilfe der Logarithmen. Man hat nämlich nur den Logarithmus des Radicanden durch den Wurzelexponenten zu dividiren u. zu dem gefundenen Quotienten den Logarithmanden zu suchen. So ist für
Wird nun zu 0,2571115 der Logarithmand gesucht so erhält man für die verlangte 5. W. 1,807638. mit einem Fehler, welcher weniger als 1 Milliontel beträgt. Will man eine Genauigkeit, welche die Logarithmentafeln nicht mehr gewähren, so ist der Binomische Lehrsatz anzuwenden. Jede Zahl nämlich läßt sich als die Summe od. der Unterschied[438] zweier anderer Zahlen darstellen, von denen die erste eine vollständige sovielte Potenz ist, als der Wurzelexponent Einheiten hat, u. jede Wurzelausziehung ist eine Potenzirung mit gebrochenem Exponenten. So ist
In einer algebraischen Gleichung versteht man unter einer W. derselben jeden, gleichviel ob reellen od. imaginären Werth, welcher, statt der gesuchten Größe in dieselbe gesetzt, den Bedingungen der Gleichungen genügt. Ist die Gleichung eine reine, wie xm = a, so ist eine der
woraus sich sogleich die Übereinstimmung beider Benennungen ergibt. Vgl. Bauer, Über die allgemeine Entwickelung aller möglichen W-n der numerischen Gleichungen, Potsdam 1810.
Adelung-1793: Quadrat-Wurzel, die · Wurzel, die · Purgier-Wurzel, die · Behen-Wurzel, die · Kubik-Wurzel, die
Brockhaus-1911: Wurzel · Khus-Khus-Wurzel · Jesus-Christus-Wurzel
Herder-1854: Wurzel [2] · Wurzel [1]
Meyers-1905: Wurzel [2] · Wurzel [3] · Wurzel [4] · Hohe Wurzel · Jesus Christus-Wurzel · Wurzel [1]
Pierer-1857: Hohe Wurzel · Falsche Wurzel einer Gleichung · Auf die Wurzel setzen
Buchempfehlung
Angelus Silesius
Cherubinischer Wandersmann
Nach dem Vorbild von Abraham von Franckenberg und Daniel Czepko schreibt Angelus Silesius seine berühmten Epigramme, die er unter dem Titel »Cherubinischer Wandersmann« zusammenfasst und 1657 veröffentlicht. Das Unsagbare, den mystischen Weg zu Gott, in Worte zu fassen, ist das Anliegen seiner antithetisch pointierten Alexandriner Dichtung. »Ich bin so groß als Gott, er ist als ich so klein. Er kann nicht über mich, ich unter ihm nicht sein.«
242 Seiten, 11.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Geschichten aus dem Sturm und Drang II. Sechs weitere Erzählungen
Zwischen 1765 und 1785 geht ein Ruck durch die deutsche Literatur. Sehr junge Autoren lehnen sich auf gegen den belehrenden Charakter der - die damalige Geisteskultur beherrschenden - Aufklärung. Mit Fantasie und Gemütskraft stürmen und drängen sie gegen die Moralvorstellungen des Feudalsystems, setzen Gefühl vor Verstand und fordern die Selbstständigkeit des Originalgenies. Für den zweiten Band hat Michael Holzinger sechs weitere bewegende Erzählungen des Sturm und Drang ausgewählt.
- Johann Karl Wezel Kakerlak oder die Geschichte eines Rosenkreuzers
- Gottfried August Bürger Münchhausen
- Friedrich Schiller Der Verbrecher aus verlorener Ehre
- Karl Philipp Moritz Andreas Hartknopfs Predigerjahre
- Jakob Michael Reinhold Lenz Der Waldbruder
- Friedrich Maximilian Klinger Geschichte eines Teutschen der neusten Zeit
424 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum