Parabel

[657] Parabel (v. gr. Parabŏle), 1) Nebeneinanderstellung, Gleichniß; daher Parabolisch, vergleichend od. gleichnißmäßig, Parabolisiren, durch Gleichnisse reden; 2) Rede od. Erzählung in einem durchgeführten Gleichniß. Die P. ist von der Allegorie darin verschieden, daß in der P. das Urbild in der Vergleichung beibehalten, in der Allegorie aber ganz verhüllt u. das Abbild an dessen Stelle gesetzt wird. Von der Fabel unterscheidet sie sich dadurch, daß sie stets aus dem Bereich des Wirklichen hergenommen wird. Die P. gehört in der Redekunst dem Lehrvortrage, in der Dichtkunst der didaktischen Poesie an. Reich an den trefflichsten P-n ist die Bibel (z.B. Nathans Bußpredigt vor David, die P. vom verlornen Sohn), wie überhaupt die Orientalische Literatur; unter den Deutschen haben bes. Herder u. Krummacher gute P-n gedichtet; 3) (Apollonische P), ein Kegelschnitt, welcher erhalten wird, indem man einen Kegel durch eine nicht durch die Spitze gehende Ebene schneidet, welche der gerade gegenüberliegenden Seitenkante des Kegels parallel ist. Sie ist eine zusammenhängende, aus zwei ins Unendliche sich erstreckenden, gegen eine mittlere Gerade symmetrischen Asten bestehende krumme Linie. Als rein geometrisch ebene Figur erklärt, ist die P. der geometrische Ort aller Punkte, welche von einem gewissen festen Punkte (Brennpunkt der P.) u. einer festen Geraden (Directrix od. Richtlinie der P.) gleichen Abstand haben. Hieraus ergibt sich, wenn Brennpunkt u. Directrix gegeben sind, die Construction der P.: a) durch geometrische Bestimmung beliebig vieler Punkte der P., welche man durch einen Zug verbindet. Man fällt nämlich vom Brennpunkt auf die Directrix ein Perpendikel, welches man über den Brennpunkt hinaus beliebig verlängert, zieht durch einen beliebigen Punkt dieses Perpendikels eine Parallele zur Directrix u. beschreibt mit dem Abstande des gewählten Punktes von der Directrix als Halbmesser aus dem Brennpunkte einen Kreis, welcher die Parallele in zwei Punkten der P. schneidet; b) durch Fadenconstruction od. mechanische Construction. Man erhält die P. durch stetige Bewegung vermittelst eines Winkelhakens, indem man einen Faden, welcher der einen Kante desselben gleich ist, mit seinen Enden im Brennpunkte u. am Endpunkte dieser Kante befestigt u. den Winkelhaken mit der anderen Kante längs der gegebenen Directrix fortbewegt, während mit einem Stifte der angespannte Faden an die erste Kante angedrückt wird. Die durch die beschriebenen Constructionen erhaltene Linie schneidet[657] das Perpendikel vom Brennpunkt auf die Directrix im Halbirungspunkte, u. dieser Punkt, welcher die P. in zwei congruente Zweige theilt, heißt der Scheitel der P., jener Perpendikel aber, ins Unendliche verlängert, die Achse der P., das Vierfache des Abstandes zwischen Scheitel u. Brennpunkt der Parameter der P. Bezeichnet man die Länge des Parameters durch p u. nimmt man die Achse der P. zur Abscissenachse, den Scheitel zum Anfang eines rechtwinkeligen Coordinatensystems, so findet sich als Scheitelgleichung der P. y² = px. Hieraus folgt als Länge der Subtangente für jeden Punkt der P. 2x, d.h. man nimmt auf der Abscissenachse nach der negativen Seite hin einen der Abscisse gleichen Abschnitt u. verbindet den Endpunkt mit dem gegebenen Punkte der P., so hat man die Tangente. Eine eben so leichte Construction der Tangente ergibt sich aus der Eigenschaft der P., daß jede Subnormale gleich dem halben Parameter ist. Zieht man ferner durch einen beliebigen Punkt der P. eine Parallele zur Achse, so werden durch dieselbe alle zu der Tangente an jenem Punkte parallelen Sehnen halbirt, daher heißt jede Parallele zur Achse ein Durchmesser der P. Aus der Quadratur der P. ist der Satz merkwürdig, daß das durch einen Bogen der P. u. die zugehörige Sehne begrenzte Segment, wenn der Anfangspunkt des Bogens im Scheitel liegt, gleich dem sechsten Theile des durch die Abscisse u. Ordinate des Endpunktes gebildeten Rechteckes ist. Liegt der Anfangspunkt des Bogens nicht im Scheitel, so gilt das Analoge, wenn man nur schiefwinklige Coordinaten, den Durchmesser durch den Anfangspunkt zur Abscissenachse, die Tangente daselbst zur Ordinatenachse macht u. statt Rechteck Parallelogramme setzt. Was die Rectification anbelangt, so ist die P. unter den Kegelschnitten der einzige, welcher sich durch einen geschlossenen Ausdruck rectificiren läßt, doch ist derselbe immerhin etwas complicirt. Unter den übrigen Gleichungen der P. verdient noch die Polargleichung der P. erwähnt zu werden (1 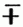cos t) u = ± p, wo der Brennpunkt als Coordinatenanfang dient. In der Physik kommt die P. als Bahn geworfener Körper vor, wenn die Schwerkraft für die verschiedenen Punkte der Bahn als parallel wirkend vorausgesetzt wird. 4) P-n höherer Ordnungen, Curven, deren Gleichung y^{m + n} = p^mxⁿ ist. Ihre Gestalt hängt davon ab, ob m u. n gerade od. ungerade Zahlen sind. Bes. merkwürdig ist die unter dem Namen der Neilschen od. Semicubischen P. (Neil, Heurät u. Fermat entdeckten sie fast zu gleicher Zeit) bekannte, deren Gleichung y³ = px² ist. Auf ihr fällt ein schwerer beweglicher Punkt in gleichen Zeiträumen gleich tief.