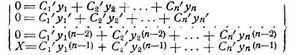Differentialgleichungen
[758] Differentialgleichungen, Gleichungen, in denen außer den unabhängigen und abhängigen Veränderlichen auch Differentialquotienten der letzteren nach den ersteren vorkommen. Man unterscheidet zunächst totale Differentialgleichungen, bei denen nur eine unabhängige Veränderliche vorkommt, und partielle Differentialgleichungen, die mehrere unabhängige Veränderliche und demgemäß partielle Differerentialquotienten nach denselben enthalten.
Die totalen Differentialgleichungen entliehen aus gewöhnlichen Gleichungen mit gewissen Konstanten (Parameter), indem man nach der unabhängigen Veränderlichen differenziert und die Parameter eliminiert, z.B.:
x2 + y2 – 2ax = 0 gibt 2x + 2y dy/dx – 2a = 0, also x2 – y2 + 2xy dy/dx = 0.
Auf Differentialgleichungen führen nicht nur viele Probleme der Mathematik, sondern auch solche der Mechanik und Physik, die für die Technik von Bedeutung sind. Ist eine Differentialgleichung gegeben, so gilt es, dieselbe zu integrieren, d.h. die gewöhnliche Gleichung zu finden, durch deren Differentiation die gegebene Differentialgleichung entlieht. Die so gefundene Gleichung, die also noch willkürliche Konstanten (Parameter) enthält, heißt das vollständige Integral der Differentialgleichung. Durch Spezialisierung der Konstanten entsteht daraus ein partikuläres Integral. Die Differentialgleichung x2 – y2 + 2xy(dy/dx) = 0 hat z.B. das vollständige Integral: x2 + y2 – 2ax = 0 (wo a ein Parameter), und ein partikuläres Integral wäre etwa:
x2 + y2 – 4x = 0 (mit a = 2).
Je nach der höchsten Ableitung, die vorkommt, werden die Differentialgleichungen in verschiedene Ordnungen eingeteilt; die betreffende Zahl ist zugleich diejenige der Konstanten des vollständigen Integrals.[758]
I. Differentialgleichungen erster Ordnung mit zwei Veränderlichen.
Dieselben enthalten nur die erste Ableitung dy/dx = y'; die vollständigen Integrale besitzen daher eine Konstante und können gedeutet werden als Gleichungen von einfachen Kurvenscharen (Integralkurven) in der Ebene. Die Differentialgleichung liefert für einen beliebigen Punkt x, y das zugehörige y', also die Richtung der durch den Punkt hindurchgehenden Scharkurve. Ist die Differentialgleichung linear, d.h. vom ersten Grad in y', so geht durch jeden Punkt der Ebene nur eine Scharkurve. Die Differentialgleichungen erster Ordnung drücken Tangentialeigenschaften der zugehörigen Kurvenscharen aus.
a) Integration der linearen Differentialgleichungen erster Ordnung. Eine solche kann (durch Multiplikation mit dx) auf die Form φ dx + ψ dy = 0 gebracht werden. Ist nun φ nur eine Funktion von x allein, ψ eine solche von y; allein, so sind »die Veränderlichen getrennt«, man kann integrieren: ∫φdx + ∫ψdy = C (vollständiges Integral) [1], S. 18, [2], S. 62. Läßt sich die Trennung der Veränderlichen nicht unmittelbar herbeiführen, so muß man sich durch Einführung neuer Veränderlicher zu helfen suchen.
α) Homogene Differentialgleichungen, solche, bei denen alle Terme der Funktionen φ und ψ vom gleichen Gesamtgrad in bezug auf x und y sind. Setzt man alsdann y – t x, also dy = tdx + xdt, so kann man die Veränderlichen trennen. Beispiel: (x2 – y2) dx + 2xydy = 0 liefert x2 + y2 – 2ax = 0 [1], S. 23, [2], S.65.
ß) Eulersche Form der Differentialgleichungen dy/dx + Py = Q, wo P und Q Funktionen von x allein sind. Auflösung:
S. 73. Die erweiterte Eulersche Form: dy/dx + Py= Oyn kommt durch die Substitution
auf die Eulersche Form zurück [2], S. 76.
γ) Exakte Differentialgleichungen heißen solche Differentialgleichungen, die genau in der Form, in der sie gegeben sind: φdx + ψdy = 0 durch Ableitung einer Funktion F(x,y) = C entstanden sind. Als Kriterium hierfür hat man:
Ist dieses erfüllt, so ist
Hierbei ist im Integral ∫φ∂x die Größe y als Konstante zu behandeln; dagegen ist die Funktion unter dem zweiten Integralzeichen nur von y abhängig. Beispiel: (x2 – 4xy – 2y2)dx + (y2 – 4xy – 2x2)dy = 0 liefert 1/3 x3 – 2x2y – 2xy2 +1/3 y3 = C [2], S. 105.
δ) Integrierender Faktor. Durch Ableiten des vollständigen Integrals F(x,y) = C entlieht immer eine exakte Differentialgleichung
Aber ∂F/∂x und ∂F/∂y können einen gemeinsamen Faktor haben, der natürlich in der gegebenen Differentialgleichung wegbleibt. Dieselbe ist daher nicht mehr exakt, kann aber durch Zufügung dieses sogenannten »integrierenden Faktors« wieder exakt gemacht werden, z.B. aus
entsteht
daher ist 1/x2 der integrierende Faktor von (x2 – y2)dx + 2xydy = 0 [2], S. 106.
ε) Die Riccatische Gleichung dy/dx + ay2 = bxm ist integrierbar, wenn m eine Zahl von der Form – 4r/2r – 1 ist (wo r eine ganze positive Zahl bedeutet). Setzt man nämlich, y = 1/2ax + z/x2; z = 1/w; x = 1/m + 3, so kommt man wieder auf eine Riccatische Gleichung, bei der jetzt aber an Stelle von m der Wert m1 = –4(r – 1)/2(r – 1) – 1 steht. So läßt sich r sukzessive erniedrigen; für r = 0 ist m = 0, und die Veränderlichen sind trennbar. Ist m von der Form – 4r/2r + 1, so läßt sich dieser Fall mittels der Substitution x = t 1/m + 1; y = 1/u auf den vorigen zurückführen [1], S. 195, [2], S.78. Ist aber m eine beliebige Zahl, so kann die Riccatische Gleichung nur vermitteln Besselscher Funktionen (s.d.) integriert werden [1], S. 199.
ζ) Ein tieferes Verständnis für die verschiedenen Methoden, die linearen Differentialgleichungen erster Ordnung zu integrieren, ermöglicht die Lehre von den Transformationsgruppen (s. Gruppentheorie) [6]. Diese Methoden erscheinen hier als Ausfluß einer allgemeineren Theorie und es wird insbesondere auch in die Bedeutung des integrierenden Faktors eine tiefere Einsicht gewonnen [6], S. 95.
b) Differentialgleichungen erster Ordnung von höherem Grad. Kommt die Ableitung p = dy/dx in höherem Grad in einer Differentialgleichung F(x,y,p) = 0 vor, so gehen durch jeden Punkt der Ebene mehrere (reelle oder imaginäre) Integralkurven. Die Kurvenschar des vollständigen Integrals f(x,y,C) = 0 besitzt alsdann eine Umhüllungskurve, die singuläre Integralkurve. Ihre Gleichung, das singuläre Integral, das im allgemeinen von den partikulären Integralen verschieden ist, erhält man entweder durch Elimination von p zwischen F = 0 und ∂F/∂p = 0 oder durch Elimination der Konstanten C zwischen f = 0 und ∂f/∂C = 0. Doch muß dieselbe noch darauf untersucht werden, ob sie wirklich ein Integral der Differentialgleichung[759] ist; die betreffende Kurve ist nämlich unter Umständen nicht eine Umhüllung, sondern der Ort von Rückkehrpunkten oder andern singulären Punkten der Integralkurven.
c) Entscheidung, ob eine gegebene Gleichung f = 0 ein vollständiges, partikuläres oder singuläres Integral der Differentialgleichung F(x,y,p) = 0 ist oder nicht.
α) Eine Gleichung f(x,y,C) = 0 mit willkürlichen Konstanten C (d.h. mit einer Konstanten, die in F = 0 nicht vorkommt) ist das vollständige Integral von F = 0, wenn durch Elimination von C aus f = 0 und
eine mit F = 0 übereinstimmende Differentialgleichung entsteht.
ß) Eine Gleichung f = 0 ohne willkürliche Konstante ist überhaupt ein Integral von F = 0, wenn bei Elimination von y und p aus f = 0;
und F = 0 auch x herausfällt.
γ) Das Integral f = 0 ohne willkürliche Konstante ist ein singuläres, wenn außerdem bei Elimination von y und p aus f = 0;
und ∂F/∂p = 0 auch x herausfällt; andernfalls ist f = 0 ein partikuläres Integral.
d) Integration von Differentialgleichungen erster Ordnung höheren Grads.
α) Ist gegeben x = f(p), so ist
womit x und y in Funktion des Parameters p gegeben sind [2], S. 92.
ß) Ist gegeben y = f(p), so ist
[2], S. 93.
γ) Clairautsche Form: y = px + f(p); vollständiges Integral y = Cx + f(C), also immer eine Geradenschar. Dieselbe umhüllt die Kurve des singulären Integrals:
[1], S. 3, [2], S. 94.
δ) Erweiterte Clairautsche Form: y = xφ(p) + f(p) gibt durch Differentiation:
also eine Eulersche Form (s. Oben a, ß).
II. Differentialgleichungen höherer Ordnung.
Eine Differentialgleichung n-Ordnung enthält die n-Ableitung von y nach x; ihr vollständiges Integral besitzt daher n willkürliche Konstanten und ist somit die Gleichung einer n-fachen Kurvenschar. Die Differentialgleichungen zweiter Ordnung stellen Krümmungseigenschaften der zugehörigen Scharkurven dar. Für die linearen Differentialgleichungen n-Ordnung (in denen y und seine Differentialquotienten nur im ersten Grad vorkommen) gilt der Satz: Sind y1 = 0, y2 = 0 ... yn = 0, n unabhängige partikuläre Integrale derselben, so ist: C1y1 + C2y2 ... Cnyn = 0 das vollständige Integral.
a) Integration der linearen Differentialgleichungen höherer Ordnung mit konstanten Koeffizienten ohne Absolutglied: y(n) + A1y(n – 1) + ... + An – 1y' + Any = 0 [1], Kap. 3, [2], Kap. 4. Es seien a1a2 ... an die Wurzeln der Hilfsgleichung: xn + A1xn – 1 + ... + An –1x + An = 0, so sind ea1x, ea2x ... eanx partikuläre Integrale und y = C1ea1x + C2ea2x ... + Cneanx das vollständige Integral.
a) Ist a1 eine r-fache Wurzel der Hilfsgleichung, so sind die zugehörigen partikulären Integrale: ea1x, xea1x ... xr –1ea1x.
ß) Sind a1 + iß1 zwei komplex konjugierte Wurzeln der Hilfsgleichung, so sind die zugehörigen partikulären Integrale: ea1x cos ß1x und ea1x sin ß1x.
b) Komplementäre Funktion. Besitzt die unter a) behandelte Differentialgleichung als Absolutglied eine Funktion von x auf der rechten Seite, so ist zunächst die Differentialgleichung mit Weglassung des Absolutglieds zu integrieren. Dem vollständigen Integral (in [1] irrtümlich komplementäre Funktion genannt) ist dann noch ein partikuläres Integral, die sogenannte komplementäre Funktion oder Störungsfunktion φ beizufügen; dieselbe ist in einzelnen Fällen leicht zu ermitteln:
a) Ist X eine ganze rationale Funktion n. Grads, so ist φ eine ebensolche Funktion mit unbestimmten Koeffizienten.
ß) Ist X eine Exponentialfunktion eax, so ist φ = ceax; wenn aber a eine Wurzel der Hilfsgleichung ist, so ist φ = exeax u.s.w.
y) Ist X eine goniometrische Funktion sin ßx oder cos ßx (oder beide zusammen), so ist φ = c1 sin ßx + cos ßx (sie muß ebenfalls mit x multipliziert werden, wenn sin ßx und cos ßx schon im vollständigen Integral vorkommen).
δ) In ähnlicher Weise ist zu verfahren, wenn X eine Funktion von x,eax, sin ßx oder cos ßx ist, z.B. eax sin ßx u.s.w. Die unbestimmten Koeffizienten von φ werden durch Einsetzen bestimmt.
c) Variation der Konstanten [1], S. 113. Ist das Absolutglied von andrer Form, als unter b) angegeben wurde, so werden im vollständigen Integral der Differentialgleichung ohne Absolutglied die Konstanten C1 C2 ... Cn als Funktionen von x betrachtet. Ihre Ableitungen C1' C2' ... Cn' bestimmen sich nun aus den Gleichungen:
[760] Die Methode ist auch auf lineare Differentialgleichungen mit veränderlichen Koeffizienten anwendbar, wenn man nur n partikuläre Integrale derselben kennt.
d) Integration von linearen Differentialgleichungen höherer Ordnung mit veränderlichen Koeffizienten. Von Wichtigkeit ist folgender Fall: (a + αx)ny(n) – A1 (a + αx)n – 1y(n –1) + ... + An – 1 (a + αx)y' + Any = X, wo A1 ... An Konstanten sind. Durch die Substitution a + αx = αet kommt man auf den unter a) behandelten Fall zurück [1], S. 28, [2], S. 199.
III. Integration von Differentialgleichungen mittels Reihen [1], Kap. 5, [2], S.219.
Wenn die seither angegebenen Methoden versagen, so schreibt man y als Reihe nach steigenden (resp. fallenden) Potenzen von x mit unbestimmten Exponenten und Koeffizienten an, setzt dieselbe in die Differentialgleichung ein und bestimmt die Koeffizienten und Exponenten durch Koeffizientenvergleichung. Statt der Reihen können auch bestimmte Integrale gute Dienste leisten [1], Kap. 7, [2], S. 236,
IV. Differentialgleichungen mit mehr als zwei Veränderlichen.
a) Ist eine einzige solche gegeben, so gelingt es in einzelnen Fällen, die Veränderlichen zu trennen [2], z.B.S. 119. Die Differentialgleichung
besitzt das transzendente Integral: arc sin x + arc sin y = arc sin t und das ihm gleichwertige algebraische
b) Der Inbegriff von mehreren Differentialgleichungen mit mehreren abhängigen Veränderlichen heißt: simultane (gleichzeitige) Differentialgleichungen. Man bestimmt eine der Veränderlichen, indem man die übrigen samt ihren Ableitungen eliminiert; hierbei hat man eventuell die gegebenen Differentialgleichungen erst noch abzuleiten [1], S. 299.
Literatur: Von den untengenannten Werken sind zum Studium in erster Linie [1] und [2] zu empfehlen. Die Werke [3], [4] und [8] handeln speziell von linearen Differentialgleichungen; [3] und [5] benutzen funktionentheoretische Hilfsmittel und eignen sich mehr zum tieferen Eindringen; [6] steht auf dem Standpunkt der Transformationsgruppentheorie. – [1] Forsyth, A.R., Lehrbuch der Differentialgleichungen, herausgegeben von H. Maser, Braunschweig 1889. – [2] Serret, J.A., Lehrbuch der Differential- und Integralrechnung, deutsch von A. Harnack, Bd. 2, 2. Hälfte, Leipzig 1885. – [3] Schlesinger, L., Handbuch der Theorie der linearen Differentialgleichungen I-II, Leipzig 1895–98. – [4] Heffter, L., Einleitung in die Theorie der linearen Differentialgleichungen mit einer unabhängigen Variabeln, Leipzig 1894. – [5] Königsberger, L., Lehrbuch der Theorie der Differentialgleichungen mit einer unabhängigen Variabeln, Leipzig 1889. – [6] Lie, S., Vorlesungen über Differentialgleichungen mit bekannten infinitesimalen Transformationen, herausgegeben von Scheffers, Leipzig 1891. – [7] Forsyth, A.R., Exakte Gleichungen und das Pfaffsche Problem, deutsch von Maser, Leipzig 1893. – [8] Klein, F., Vorlesungen über lineare Differentialgleichungen zweiter Ordnung, Leipzig 1894. – [9] Liebmann, H., Lehrbuch der Differentialgleichungen, Leipzig 1901. – [10] Schlesinger, L., Einführung in die Theorie der Differentialgleichungen mit einer unabhängigen Variabeln, 2. Aufl., Leipzig 1904.
Die partiellen Differentialgleichungen entstehen durch partielle Ableitung einer gewöhnlichen Gleichung nach den unabhängigen Veränderlichen und Elimination von Funktionen; z.B. aus z = φ (x2 + y2 + z2) erhält man
Durch Elimination von φ' entsteht
– Geometrisch gedeutet, gehört eine partielle Differentialgleichung nicht einer Schar von Flächen, sondern einer Familie von solchen an, d. h dem Inbegriff aller Flächen, die eine gewisse Eigenschaft besitzen.
Beispiele: αp + ßq = γ Differentialgleichung aller Zylinderflächen, deren Mantellinien der Geraden x/α = y/ß = z/y parallel sind; p (x – a) + q (y – b) = z – c Differentialgleichung aller Kegelflächen mit Mittelpunkt (a/c, b/c); px + qy = 0 Differentialgleichung aller Konoidflächen mit der xy-Ebene als Richtebene und der z-Achse als Leitgerade; qx – py = 0 Differentialgleichung aller Umdrehungsflächen mit der z-Achse als Drehungsachse; rt – s2 = 0 Differentialgleichung aller abwickelbaren Flächen u.s.w.
Eine partielle Differentialgleichung integrieren, heißt die gewöhnliche Gleichung suchen, durch deren partielle Ableitung erstere entstanden ist. Bei linearen partiellen Differentialgleichungen erster Ordnung genügt es, zwei partikuläre Integrale u und v zu kennen; denn alsdann ist u = φ(v) die allgemeine Lösung, wo φ eine willkürliche Funktion ist. Die Flächenscharen u = c1 und v = c2 schneiden sich in Kurven, die als Charakteristiken der betreffenden Flächenfamilie bezeichnet werden und deren je unendlich viele auf einer Fläche der Familie liegen. In obigem Beispiel sind die Charakteristiken
horizontale Kreise, die ihre Mittelpunkte auf der z-Achse haben; je unendlich viele derselben liegen auf einer Umdrehungsfläche.
Die Integration der linearen partiellen Differentialgleichungen erster Ordnung von der Form Pp + Qq = R (wo P, Q und R Funktionen von xyz sind) erfolgt durch Integration der simultanen totalen Differentialgleichungen: dx/P = dy/Q = dz/R. Die vollständigen Integrale derselben u = c1 und v = c2 sind partikuläre Integrale der partiellen Differentialgleichung, daher u = φ(v) die allgemeine Lösung. Partielle Differentialgleichungen zweiter Ordnung kommen[761] vielfach in der mathematischen Physik vor (s. [5]); z.B. in der Theorie der Saitenschwingungen die Differentialgleichung r = a2t mit der Lösung z = φ(y + ax) + φ(y – ax) und bei dei Wärmebewegung die Differentialgleichung: p = a2t mit den partikulären Integralen
e–a2a2x cos α (y – λ) und e–a2a2x sin α (y – λ)
wo α und λ Konstanten sind. Wegen der Zeichen (p, q, r, t) vgl. Differentialquotient.
Literatur: Von den hier angeführten Werken beschränken sich [3] und [4] auf partielle Differentialgleichungen erster Ordnung; [4] bedient sich der Berührungstransformationen (s. Gruppentheorie). In [5] finden sich Anwendungen auf mathematische Physik. – [1] Forsyth, Lehrbuch der Differentialgleichungen, deutsch von Maser, Braunschweig 1889, Kap. 9 und 10. – [2] Serret, J.A., Lehrbuch der Differential- und Integralrechnung, Bd. 2, zweite Hälfte, Leipzig 1885, Kap. 6. – [3] Mansion, Theorie der partiellen Differentialgleichungen erster Ordnung, 2. Aufl., Berlin 1892. – [4] Goursat, E., Vorlesungen über die Integration der partiellen Differentialgleichungen erster Ordnung, deutsch von Maser, Leipzig 1893. – [5] Weber, A., Die partiellen Differentialgleichungen der mathematischen Physik, Bd. 1 und 2, Braunschweig 1900–01. – [6] Dienger, J., Integration der partiellen Differentialgleichungen, Stuttgart 1862. – [7] Lagrange, J.L., und Cauchy, A.L., Zwei Abhandlungen zur Theorie der partiellen Differentialgleichungen erster Ordnung, herausgegeben von G. Kowalewski, Leipzig 1901. – [8] Pfaff, J.F., Allgemeine Methode, partielle Differentialgleichungen zu integrieren, herausgegeben von G. Kowalewski, Leipzig 1902. – [9] v. Weber, E., Vorlesungen über das Pfaffsche Problem und die Theorie der partiellen Differentialgleichungen 1. Ordnung, Leipzig 1900.
Wölffing.
Lueger-1904: Differentialgleichungen der Bewegung
Buchempfehlung
Stifter, Adalbert
Bunte Steine. Ein Festgeschenk 1852
Noch in der Berufungsphase zum Schulrat veröffentlicht Stifter 1853 seine Sammlung von sechs Erzählungen »Bunte Steine«. In der berühmten Vorrede bekennt er, Dichtung sei für ihn nach der Religion das Höchste auf Erden. Das sanfte Gesetz des natürlichen Lebens schwebt über der idyllischen Welt seiner Erzählungen, in denen überraschende Gefahren und ausweglose Situationen lauern, denen nur durch das sittlich Notwendige zu entkommen ist.
230 Seiten, 9.60 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Romantische Geschichten. Elf Erzählungen
Romantik! Das ist auch – aber eben nicht nur – eine Epoche. Wenn wir heute etwas romantisch finden oder nennen, schwingt darin die Sehnsucht und die Leidenschaft der jungen Autoren, die seit dem Ausklang des 18. Jahrhundert ihre Gefühlswelt gegen die von der Aufklärung geforderte Vernunft verteidigt haben. So sind vor 200 Jahren wundervolle Erzählungen entstanden. Sie handeln von der Suche nach einer verlorengegangenen Welt des Wunderbaren, sind melancholisch oder mythisch oder märchenhaft, jedenfalls aber romantisch - damals wie heute. Michael Holzinger hat für diese preiswerte Leseausgabe elf der schönsten romantischen Erzählungen ausgewählt.
- Ludwig Tieck Die beiden merkwürdigsten Tage aus Siegmunds Leben
- Karoline von Günderrode Geschichte eines Braminen
- Novalis Heinrich von Ofterdingen
- Friedrich Schlegel Lucinde
- Jean Paul Die wunderbare Gesellschaft in der Neujahrsnacht
- Adelbert von Chamisso Peter Schlemihls wundersame Geschichte
- E. T. A. Hoffmann Der Sandmann
- Clemens Brentano Die drei Nüsse
- Ludwig Achim von Arnim Der tolle Invalide auf dem Fort Ratonneau
- Wilhelm Hauff Jud Süss
- Joseph von Eichendorff Das Schloß Dürande
442 Seiten, 16.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum