Maxĭmum

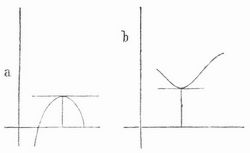
[480] Maxĭmum und Minĭmum (lat., »das Größte« und »das Kleinste«), der größte, bez. der kleinste Wert unter einer Anzahl von Werten. In der Mathematik ist Maximum, bez. Minimum einer Funktion jeder Wert der Funktion, der größer (>), bez. kleiner (<) ist als die ihm benachbarten Werte. Schärfer ist folgende Erklärung: die Funktion f(x) der reellen Veränderlichen x hat für x = x₀ ein Maximum, bez. Minimum, wenn es eine solche positive Zahl δ gibt, daß für jede Größe h, die zwischen -δ und +δ liegt, f(x₀+h) < f(x₀), bez. > f(x₀) wird. Für M. u. M. hat man auch die gemeinsame Bezeichnung Extremwert oder Extrem (äußerster Wert). Stellt man die Funktion graphisch dar, indem man f(x) = y setzt und x u. y als rechtwinkelige Koordinaten (s. d.) der Punkte einer Ebene deutet, so steigt ihre Bildkurve von dem Maximum an u. fällt nachher (Fig. a), beim Minimum ist es umgekehrt (Fig. b).

Für jedes Extrem ist daher die Tangente der Kurve parallel der Abszissenachse. In Euklids Elementen findet sich in Buch 6, Nr. 27, das erste Beispiel eines Maximums in dem Satz: Unter allen Rechtecken von gegebenem Umfange hat das Quadrat den größten Inhalt. Ist 4 a der Umfang des Rechtecks, x die eine Seite, also 2a-x die andre, so wird der Inhalt J = x(2a-x), es soll mithin die Funktion x(2a-x) der Veränderlichen x ein Maximum werden. Die Lösung der Aufgabe ergibt sich hier einfach durch Untersuchung der quadratischen Gleichung: J = x(2 a-x); aus der man durch Auflösung nach x (s. Gleichung) erhält: x = a ± √a²-J. Da nämlich die Quadratwurzel aus einer negativen Zahl weder eine positive noch eine negative, sondern eine imaginäre Zahl ist (s. Komplexe Zahlen), so darf J nicht größer als a² werden, sondern kann höchstens gleich a² sein. Dieses Maximum von J tritt ein für x = a, wo auch 2a-x = a wird, also für das Quadrat. Lösungen einzelner Maximums- und Minimumsaufgaben finden sich außer bei Euklid auch bei Archimedes, besonders aber bei Apollonius, der zuerst die Bestimmung der Extreme als selbständige Aufgabe hinstellte. Eine allgemeine Methode zur Lösung solcher Aufgaben hat erst Fermat gegeben und dadurch die Erfindung der Differentialrechnung vorbereitet. Nach seiner Methode wäre jenes Beispiel folgendermaßen zu behandeln: J als Funktion von x verschwindet für x = O und x = 2 a, zwischen diesen beiden Werten von x muß also einer x₀ liegen, dem ein Extrem von J entspricht. Zu jedem Wert u vor x₀ wird ein Wert v hinter x₀ gehören derart, daß J für x = u und für x = v denselben Wert besitzt, so daß also u(2a-u) = v(2a-v) oder 2a(u-v) = u²-v² wird. Da u, v voneinander verschieden sind, so kann man mit u-v dividieren und bekommt: 2a = u+v. Je mehr sich nun u dem Wert x₀ nähert, zu dem das Extrem von J gehört, um so mehr nähert sich auch v diesem Wert und für u = x₀ wird auch v = x₀, folglich ist 2a = 2x₀, x₀ = a; aus a²-J = a²-x(2a-x) = (a-x)² ergibt sich endlich, daß J für x < a und für x > a stets < a² ausfällt, daß also J für x = a ein Maximum hat. Nach Erfindung der Differentialrechnung ergab sich, daß für jeden Wert von x, dem ein Extrem der Funktion f(x) entspricht, die erste Ableitung f¹(x) von f(x) verschwinden muß; ob umgekehrt ein x, für das f¹(x) verschwindet, wirklich ein Extrem von f(x) und ob es ein Maximum oder Minimum liefert, erfordert noch eine besondere Untersuchung, die durch Anwendung der Taylorschen Reihe (s. d.) sehr erleichtert wird. Für die Schule ist jedoch die Fermatsche Methode immer noch die zweckmäßigste (vgl. Duhamel, Mémoire sur la méthode des maxima et minima de Fermat, Par. 1864; Wiecke, Lehrproben, geometrische und algebraische Betrachtungen über M. u. M., Berl. 1894). Die Übertragung der Begriffe M. u. M. auf Funktionen mehrerer Veränderlichen macht keine Schwierigkeit, wohl aber die Entscheidung darüber, unter welchen Bedingungen wirklich ein Maximum oder Minimum eintritt; diese Frage ist erst in neuester Zeit durch Scheeser, Stolz, A. Mayer u. a. einwandfrei beantwortet worden. Vgl. O. Stolz, Grundzüge der Differential- und Integralrechnung, Teil 1 (Leipz. 1893); manche Lehrbücher der Differentialrechnung sind in diesem Punkte nicht ganz korrekt. Eine noch allgemeinere Art von M. u. M. ist Gegenstand der Variationsrechnung (s. d.).